二叉樹的相關介面實現
阿新 • • 發佈:2018-11-11
一、4.1二叉樹鏈式結構的遍歷
所謂遍歷(Traversal)是指沿著某條搜尋路線,依次對樹中每個結點均做一次且僅做一次訪問。訪問結點所做
的操作依賴於具體的應用問 題。 遍歷是二叉樹上最重要的運算之一,是二叉樹上進行其它運算之基礎。
前序/中序/後序的遞迴結構遍歷:是根據訪問結點操作發生位置命名
- NLR:前序遍歷(Preorder Traversal 亦稱先序遍歷)——訪問根結點的操作發生在遍歷其左右子樹之前。
- LNR:中序遍歷(Inorder Traversal)——訪問根結點的操作發生在遍歷其左右子樹之中(間)。
- LRN:後序遍歷(Postorder Traversal)——訪問根結點的操作發生在遍歷其左右子樹之後。
由於被訪問的結點必是某子樹的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解釋為
根、根的左子樹和根的右子樹。NLR、LNR和LRN分別又稱為先根遍歷、中根遍歷和後根遍歷。
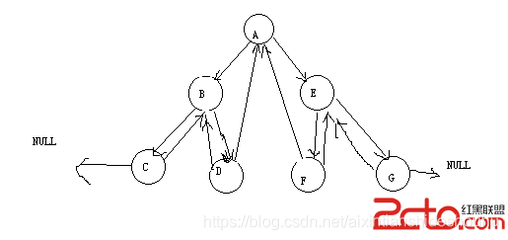
層序遍歷:除了先序遍歷、中序遍歷、後序遍歷外,還可以對二叉樹進行層序遍歷。設二叉樹的根節點所在
層數為1,層序遍歷就是從所在二叉樹的根節點出發,首先訪問第一層的樹根節點,然後從左到右訪問第2層
上的節點,接著是第三層的節點,以此類推,自上而下,自左至右逐層訪問樹的結點的過程就是層序遍歷。
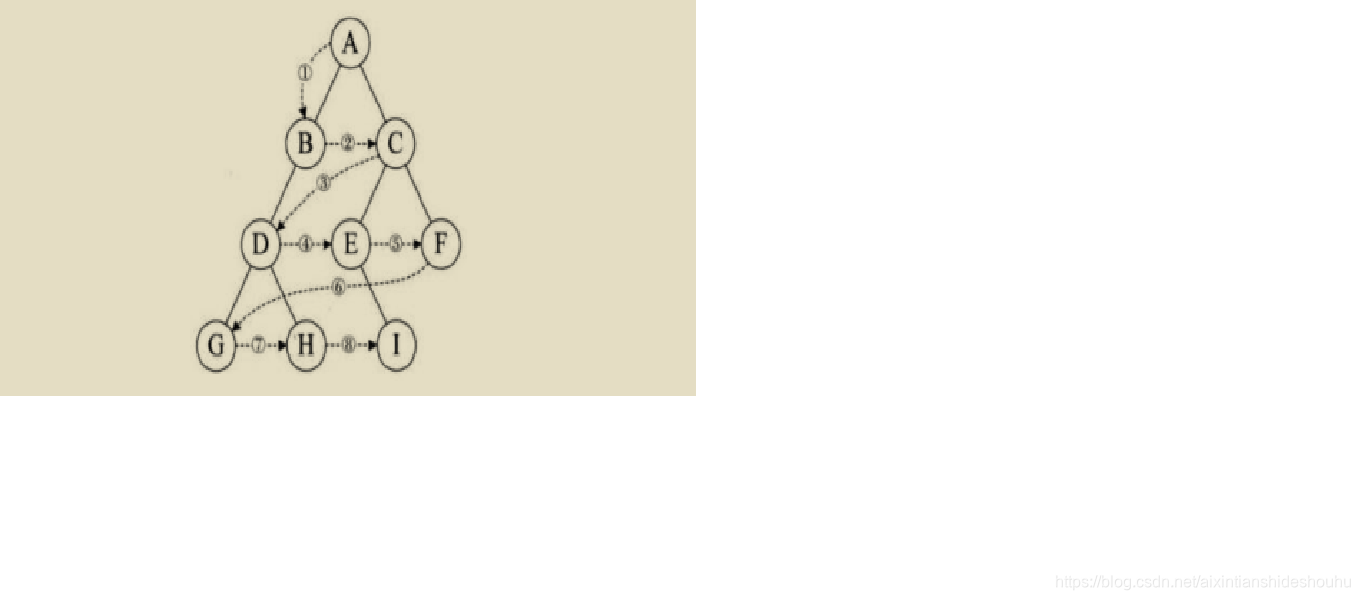
二叉樹的介面實現
1、標頭檔案
#pragma once #include<stdio.h> #include<assert.h> #include<stdlib.h> typedef char BTType; typedef struct BTNode { BTType _data; struct BTNode* _left; struct BTNode* _right; }BTNode; typedef BTNode* QUDataType; typedef struct QueueNode { QUDataType _data; struct QueueNode* _next; }QueueNode; typedef struct Queue { QueueNode* _front; QueueNode* _rear; }Queue; void QueueInit(Queue* q); void QueueDestory(Queue* q); void QueuePush(Queue* q, QUDataType x); void QueuePop(Queue* q); int QueueSize(Queue* q); int QueueEmpty(Queue* q); QUDataType QueueFront(Queue* q); QUDataType QueueBack(Queue* q); typedef BTNode* STDataType; typedef struct Stack { STDataType* _a; int _top; int _capacity; }Stack; void StackInit(Stack* ps, int n); void StackDestory(Stack* ps); void StackPush(Stack* ps, STDataType x); void StackPop(Stack* ps); STDataType StackTop(Stack* ps); int StackSize(Stack* ps); int StackEmpty(Stack* ps); void StackPrint(Stack* ps); BTNode* CreatBTree(BTType* str, int* n); int BinaryTreeSize(BTNode* root);//二叉樹節點個數 int BinaryTreeLeafSize(BTNode* root);//兒叉樹的葉子節點個數 int BinaryTreeLevelKSize(BTNode* root, int k);//二叉樹第k層葉子節點個數 BTNode* BinaryTreeFind(BTNode* root, BTType val); //遞迴遍歷二叉樹 void BinaryTreePrevOrder(BTNode* root); void BinaryTreeInOrder(BTNode* root); void BinaryTreePostOrder(BTNode* root); //二叉樹的層序遍歷 void BinaryTreeLevelOrder(BTNode* root); //非遞迴遍歷二叉樹 void BinaryTreePrevOrderNonR(BTNode* root); void BinaryTreeInOrderNonR(BTNode* root); void BinaryTreePostOrderNonR(BTNode* root); void Test();
2、定義檔案
#include "Tree.h" BTNode* BuyTreeNode(BTType x) { BTNode* newnode = (BTNode*)malloc(sizeof(BTNode)); newnode->_data = x; newnode->_left = NULL; newnode->_right = NULL; return newnode; } BTNode* CreatBTree(BTType* arr, int* n) { if (arr[*n] != '#') { BTNode* root = BuyTreeNode(arr[*n]); (*n)++; root->_left = CreatBTree(arr, n); (*n)++; root->_right = CreatBTree(arr, n); return root; } else { return NULL; } } int BinaryTreeSize(BTNode* root) { if(root == NULL) return 0; return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1; } int BinaryTreeLeafSize(BTNode* root) { if(root == NULL) return 0; if(root->_left == NULL && root->_right == NULL) return 1; return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right); } int BinaryTreeLevelKSize(BTNode* root, int k) { if(root == NULL) return 0; if(root->_left == NULL && root->_right == NULL) return 1; return BinaryTreeLevelKSize(root->_left, k-1) + BinaryTreeLevelKSize(root->_right, k-1); } BTNode* BinaryTreeFind(BTNode* root, BTType val) { BTNode* ret = NULL; if(root == NULL) return NULL; if(root->_data == val) return root; ret = BinaryTreeFind(root->_left,val); if(ret != NULL) return ret; ret = BinaryTreeFind(root->_right, val); if(ret != NULL) return ret; return NULL; } void BinaryLevelOrder(BTNode* root) { Queue s; QueueInit(&s); if(root != NULL) { QueuePush(&s, root); } while(QueueEmpty(&s) == 1) { BTNode* front = QueueFront(&s); QueuePop(&s); printf("%s ", front->_data); if(front->_left != NULL) QueuePush(&s, front->_left); if(front->_right != NULL) QueuePush(&s, front->_right); } printf("\n"); } //非遞迴前序遍歷二叉樹的思想為:a.訪問他的左路節點b.訪問左路節點的右子樹 //將所有左路節點入棧的同時並訪問,然後拿出棧頂節點,同時出棧頂節點,此時在訪問出棧節點的右孩子, //若右孩子為空直接棧頂節點,若不為空繼續入站,訪問出棧節點的左路節點和左路節點的右子樹, void BinaryTreePrevOrderNonR(BTNode* root) { BTNode* cur = root; BTNode* top = NULL; Stack st; StackInit(&st, 3); while(cur != NULL || StackEmpty(&st) != 0) { while(cur != NULL) { printf("%c ", cur->_data); StackPush(&st, cur); cur = cur->_left; } top = StackTop(&st); StackPop(&st); cur = top->_right; } printf("\n"); } //中序遍歷的思路和前序遍歷非遞迴很相似,也是分為左路節點和左路節點的右子樹 //首先把左路節點入棧,不訪問,當左路節點沒有左左孩子時,那出棧頂節點並且訪問,讓後出棧頂接節點 //然後把棧節點的右孩子入棧,並且繼續上面的過程。 void BinaryTreeInOrderNonR(BTNode* root) { BTNode* cur = root; BTNode* top = NULL; Stack st; StackInit(&st, 3); while(cur != NULL || StackEmpty(&st) != 0) { while(cur != NULL) { StackPush(&st, cur); cur = cur->_left; } top = StackTop(&st); StackPop(&st); printf("%c ", top->_data); cur = top->_right; } printf("\n"); } //後序遍歷的非遞迴遍歷時,要判讀它的右路節點是否已經被訪問過,如果沒有訪問過就訪問。 //首先把根節點入棧,如果根節點的左子樹和右子樹不存在,或者根節點的左子樹和右子樹已經 //訪問過,直接拿出根節點訪問,然後出棧節點,標記為上一個輸出節點的prev,在把此時的站棧頂節點 //作為當前節點,若果不滿足條件,就把根節點的左子樹和右子樹一次入棧,當前節點重置為棧頂節點,然後重複操作 void BinaryTreePostOrderNonR(BTNode* root) { BTNode* top = NULL; BTNode* prev = NULL; BTNode* cur = root; Stack st; StackInit(&st,3); while(cur != NULL || StackEmpty(&st) != 0) { while(cur != NULL) { StackPush(&st, cur); cur = cur->_left; } top = StackTop(&st); if(top->_right == NULL || top->_right == prev) { printf("%c ",top->_data); StackPop(&st); prev = top; } else { cur = top->_right; } } } void BinaryTreePrevOrder(BTNode* root) { if(NULL == root) return; printf("%c ", root->_data); BinaryTreePrevOrder(root->_left); BinaryTreePrevOrder(root->_right); } void BinaryTreeInOrder(BTNode* root); { if(NULL == root) return; BinaryTreeInOrder(root->_left); printf("%c ",root->_data); BinaryTreeInOrder(root->_right); } void BinaryTreePostOrder(BTNode* root); { if(NULL == root) return; BinaryTreePostOrder(root->_left); BinaryTreePostOrder(root->_right); printf("%c ", root->_data); } void Test() { int i = 0; char* arr = "ABD##E#H##CF#G##"; BTNode* tree = CreatBTree(arr,&i); printf("%d\n", BinaryTreeLeafSize(tree)); }
