以下程式碼為第一步求最大前後綴所含字元個數的程式碼：

首先我們明確：next[i]存放的是前i個字元組成的字串的最大相同前後綴長度

 1     public static int[] kmpnext(String str){　　　　　　　　　　　　　　//引數為要求的字串str
 2         int[] next = new int[str.length()];　　　　　　　　　　　　　　 //新建一個next陣列，每一位存放對應的前n位組成的子字串的最大前後綴相同元素個數
 3         next[0] = 0;　　　　　　　　　　　　　　　　　　　　　　　　　　　　 //第一位沒有前後綴，故為0
 
 4         for(int i = 1,j = 0; i < str.length(); i++){　　　　　　　　　 //從第二位開始，依次求出所求的值
 5             while(j > 0 && str.charAt(j) != str.charAt(i)){　　　　　//重要，下面詳細解釋此處
 6                 j = next[j - 1];
 7             }
 8             if(str.charAt(i) == str.charAt(j)){　　　　　　　　　　　　 //上一輪迴圈已經比較過了前j位與後j位相同，此時若第j+1位，即索引位j的值與索引為i的值相同，那麼在這一輪迴圈中，新字串的最大前後綴就是上一輪的+1
 
 9                 j++;
10             }
11             next[i] = j;　　　　　　　　　　　　　　　　　　　　　　　　　　 //將所求的值j存放到對應位置
12         }
13         return next;
14     }

while(j>0 && str.charAt(j) != str.charAt(i))的意思是:

　　此時j的值為上一輪迴圈當中存放在next[i]中的值，即上一輪迴圈中前i位的最大前後綴的值，

　　此時迴圈+1，即比較新增加的一位與字首中新增加的一位是否相等，相等的話執行j++

　　不等的話執行j=next[j-1]；

j=next[j-1]是這段程式碼中最難理解的部分，下面為解釋：

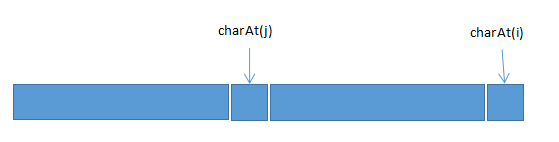
　　此時發現charAt(j) != cjarAt(i),我們將目光放在索引為j之前的子字串中：

　　改變了j的值後，圖示的兩塊橘色矩形為相同序列，

　　我們再比較新位置上的charAt(j)與charAt(i)是否相等即可，如果不相等則利用j=next[j-1]繼續縮小j的值。