轉自：《編碼的奧祕》    第十三章

               在你確信繼電器可以連線起來以構成二進位制加法器後，你可能會問： “減法器如何實現呢？”本章將會為你解答這個問題，且提出這個問題也表明你有了一定的理解力。減法和加法在某些方面是互為補充的，但兩種計算的機制不同。加法從最右邊一列向最左邊一列計算，每一列的進位都加到下一列中去。減法不用進位，相反，要用到借位—一種本質上與加法不同的機制。

              例如，讓我們看一道典型的不斷借位的減法題目：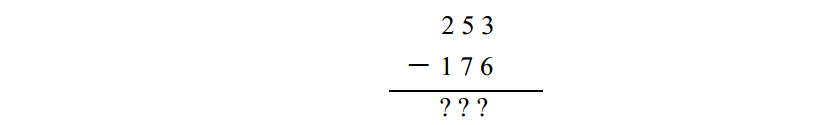

              要做這道題，從最右邊一列開始。首先， 6比3大，所以需要從 5借1 ，這樣就變成了 1 3減6，結果是 7。由於從 5借了 1 ， 5就變成了 4， 4比7小，所以繼續從 2借1 ， 1 4減7等於7。 2被借1 後成為1 ， 1 減1 為0，所以最後結果是 7 7：

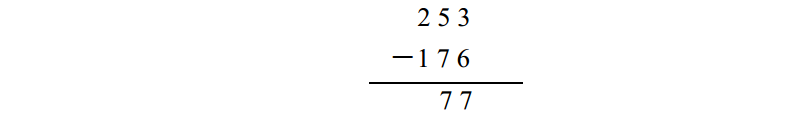
            如何用邏輯閘來實現這看似不合常理的邏輯呢？

            我們不會直接用這種方法，代替的是用一個小技巧，使不通過借位來實現減法。這會是一個使大家都滿意的好辦法。詳細地瞭解減法的完成是很有用的，因為它和用二進位制編碼在計算機中儲存負數的機制有很大聯絡。

             為解釋這樣的工作，需要清楚地指明兩個運算元，即減數和被減數。減數從被減數中去掉後，結果是二者之差：

             要想不借位，首先將減數從 9 9 9中減去：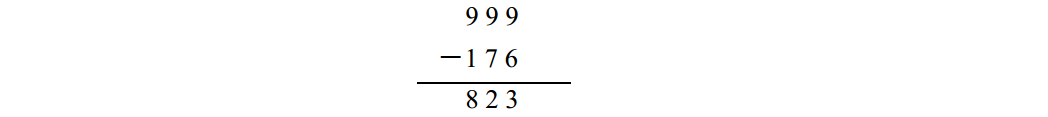

           這裡用 9 9 9是因為運算元是 3位，如果是 4位數，就用 9 9 9 9。把一個數從一串 9中減去得到的結果稱為 9的補數或補碼。 1 7 6的9的補數是 8 2 3，反之， 8 2 3的9的補數是 1 7 6。這樣做的好處在於，無論減數是什麼，計算 9的補數永遠不需要借位。

           在計算出減數的 9的補數之後，把它加到原來的被減數上：

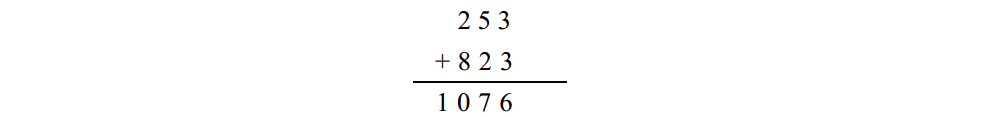
          最後，你再加１並且減去 1 0 0 0：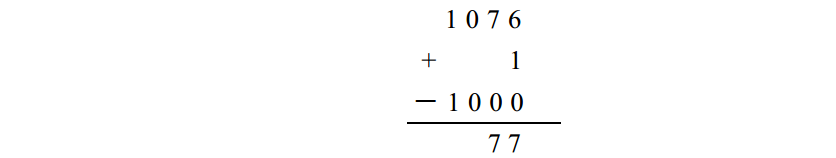

         這樣就得到結果了。答案和以前一樣，且你根本不用借位。

         這是什麼原理呢？原來的減法題目是：

         表示式加一個數再減同一個數得到的結果是一樣的。所以先加上 1 0 0 0，再減去 1 0 0 0：
         這個式子等同於下面的式子：

         再按如下方式重新組合：

         
         這與前面描述過的用 9的補數進行的計算是一致的。雖然用了兩個減法和兩個加法來代替一個減法，但是也因此省去了討厭的借位。

          但是，如果減數比被減數大怎麼辦呢？例如如下計算：

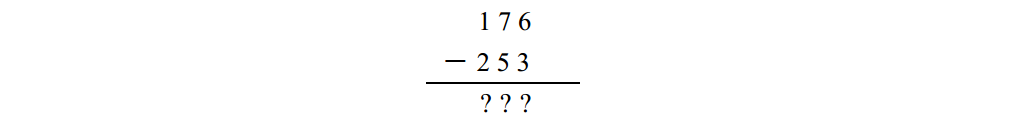
          通常情況下，你看到這個式子後可能會說： “減數比被減數大隻需交換兩數位置，再做減法，然後給結果取個相反數。 ”於是你在腦子裡交換了它們的位置，並求出了答案：

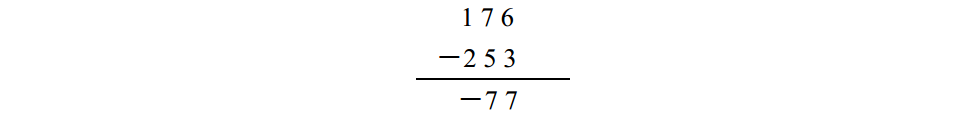
          要省去借位來做這道題和前面的例子有所不同。首先你要求出 2 5 3的9的補數，即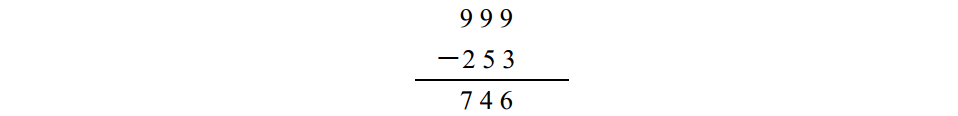

           再把該補數和原來的被減數相加：

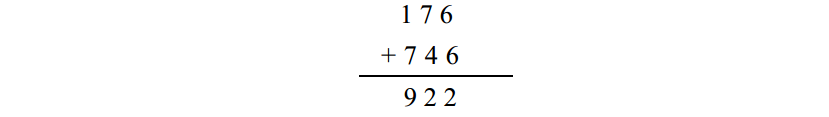
          這時候，按照上一道題的步驟，你應該對其加 1 再減去 1 0 0 0，但在本題中，這種方法不會生效。如果你還按這種步驟做，就需要從 9 2 3中減去 1 0 0 0，這又導致了借位。

         既然實際上前面已經加了 9 9 9，這裡再減去 9 9 9：

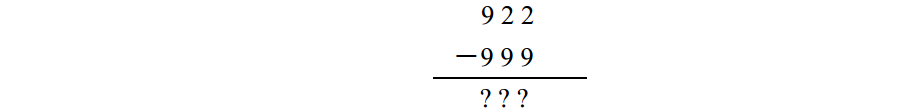
         當做到這一步時，可看出結果是個負數，故需要交換兩數位置，不過這樣再做減法時已不需要借位，答案如預期所料：

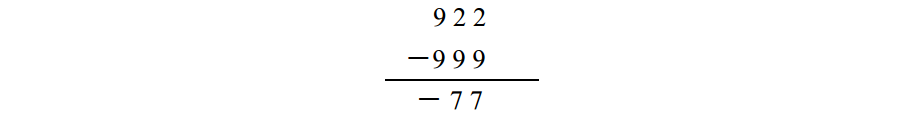
          同樣的方法可用於二進位制數減法，而且會比十進位制數減法來得簡單。讓我們看看該如何做。

          原來的減法題目是：

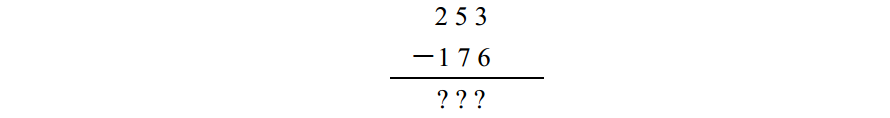
          當把這些數轉化為二進位制數時，問題變成：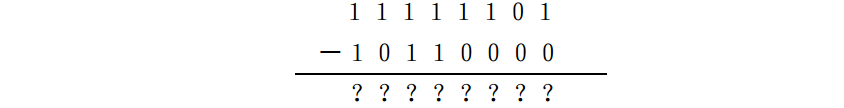

          步驟1 用 11111111減去減數：

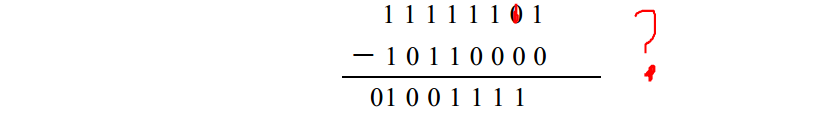
           當計算十進位制數減法時，減數是從一串 9中減去，得到稱為 9的補數的結果。對於二進位制數減法，減數從一串 1 中減去，差稱為 1 的補數。但請注意，求1 的補數實際上並不需要做減法，因為 1 的補數中，原來的 0變成 1 ，原來的 1 變成 0，所以， 1 的補數有時也稱為 相反數 或反碼 。（你是否還記得第 11 章中反向器的作用是把 0變成1 ，把1 變成0。 ）

           步驟2 把步驟1 中求得的補數和被減數相加：

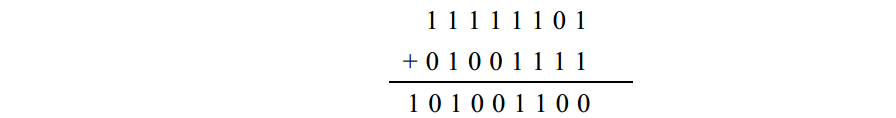
           步驟3 對結果加 1 ：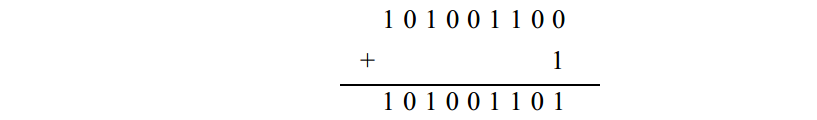

           步驟4 減去1 0 0 0 0 0 0 0 0（ 2 5 6）：

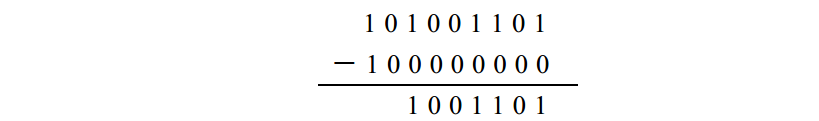
           該結果就是十進位制數 7 7。

           現在把兩數顛倒位置後再做一遍。在十進位制中，減法題目對應於：

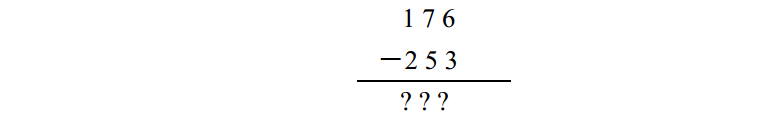
           而在二進位制中，即是：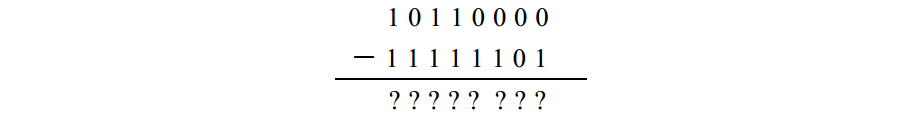

          步驟1 從11111111中減去減數。得到補數：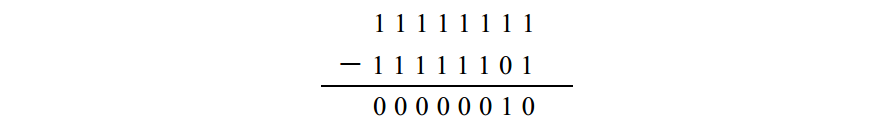
           步驟2 把步驟1 中的補數和被減數相加：

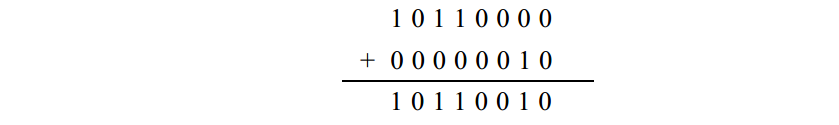
            現在， 11111111 必須再從結果中減掉。當減數比被減數小時，可以通過先加 1 再減去1 0 0 0 0 0 0 0 0來達到此目的。但現在這樣做卻會用到借位。所以，我們先用 11111111 減去步驟 2中的結果：

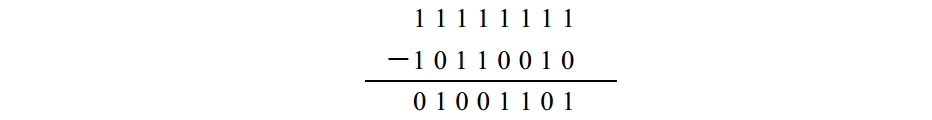
          這實際上是對步驟 2中得到的結果取反。最後的結果是 7 7，而真正的答案應該是－ 7 7。

          現在，已經可以改進加法機使它既能執行加法操作亦能執行減法操作。為使簡便起見，這個加 /減法機只執行被減數大於減數的減法操作，即差為正數的操作。

           該加法機的核心部件是由邏輯閘整合的 8位全加器：

             前面講過輸入 A0～ A 7及 B 0～ B 7連線到開關上，用於表示 8 位運算元。進位輸入端接地。S0～ S 7連線 8 個燈泡，用於表示加法的和。由於和可能會是 9位數，進位輸出端也連了一個燈泡。

             控制面板如下圖所示：
           上圖中，開關被設為 1 8 3 （或 1 0 11 0 1 11 ）和 2 2 （或 0 0 0 1 0 11 0） ，產生的結果是 2 0 5 或11 0 0 11 0 1 )。用於加 /減法的新的控制面板有一點兒修改，它包含了一個用於選擇做加法還是做減法的額外開關。

             如圖所示，當這個開關向下時表示選擇加法運算，反之是選擇減法運算。此外，只有最右邊的 8個燈泡用於表示結果，第九個燈泡用來標識上溢 /下溢，它指明瞭一個不能用 8個燈泡表示的數。當加法操作得到的和大於 2 5 5（稱為上溢）或減法計算中出現一個負數（下溢）時，這個燈泡就會亮。減數比被減數大時，結果就是一個負數。

           這個加法機主要增加了一個求 8位二進位制數的補數的電路。由於一個數的補數就是取其每一位的相反數，所以這個電路看起來很簡單，就是 8個反向器而已。

           該電路存在一個問題，就是它不分情況地對輸入求反。我們需要一臺既能做加法又能做減法的機器，而此電路只有做減法時才取反。對它進行一下改進，如下圖所示：

              圖中標識為“取反”的訊號輸入到每一個異或門中。回憶一下異或門的功能：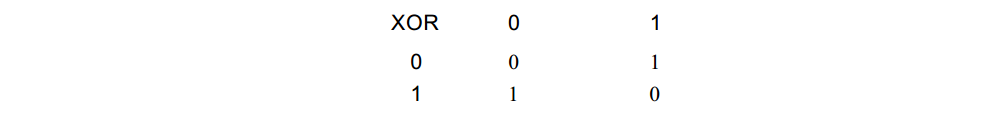
            如果“取反”訊號為 0 ，則異或門的 8 個輸出和 8 個輸入是相同的。例如，如果輸入是0 11 0 0 0 0 1 , 則輸出也是 0 11 0 0 0 0 1 ；若“取反”訊號為 1 ，則輸出取反。例如，當輸入是0 11 0 0 0 0 1 時，輸出為 1 0 0 1111 0。讓我們把 8個異或門整合到一個盒子裡，稱為求補器：
          求補器、 8位加法器及一個異或門可按下圖連線：
         注意上圖中有 3個訊號都標識為“ S U B”，這是加 /減法轉換開關。當該訊號為 0時做加法，為1 時做減法。做減法時， B 輸入在送入加法器之前先求補。此外，做減法時，通過設定加法器的進位輸入端 ( C I )為1 ，使由加法器得到的結果加 1 。對加法而言，求補電路沒有起作用，C I輸入也就是 0。

         “ S U B”訊號及加法器的 C O輸出作為異或門的輸入來控制表示上溢 /下溢的小燈泡。如果“ S U B”訊號為 0（表示做加法），則當 C O輸出為 1 時燈泡點亮，這表示加法的和大於 2 5 5。

         當做減法時，如果被減數大於減數，則加法器的 C O端正常輸出 1 ，這表示在減法的最後一步中要減去 1 0 0 0 0 0 0 0 0。所以，只有當加法器的 C O輸出為 0時，上溢 /下溢燈泡才被點亮。這時減數大於被減數，差是個負數。上面這個加 /減法器現在還不能表示負數。

         你一定興致勃勃地想知道該如何實現減法了。
         本章一直在談論負數，但沒有指出二進位制負數的表示方法。你可能會認為它的表示和十進位制負數一樣，只需在數的前面加個負號。例如，－ 7 7在二進位制中寫成－ 1 0 0 11 0 1 。你當然可以這麼表示，但別忘了用二進位制數的目的在於只用 0和1 表示所有的東西，當然也包括一個小小的負號了。

         你可以用某一位代替負號，當該位為 1 時就表示負數，為 0時表示正數，這似乎也是可行的。但還有一種方法，它不僅能表示負數，而且還很適於把正數和負數相加到一起。這種方法的不足之處是你必須提前決定數字需要多少位。

         通常用來表示正、負數的方法的好處是這種方法能表示所有的正數、負數。我們把 0想象成向一個方向延伸的無窮的正數流和向另一個方向延伸的無窮的負數流的中點：

          但是 ,如果並不需要無限大或無限小的數，而是完全可以確定計算中所遇到的數的範圍，情況便有所不同了。

          下面來看看帳戶的例子，人們有時可以在帳戶上看到負數。假設帳戶上從來沒有超過$ 5 0 0的存款， 而銀行給我們的預支額是 $ 500 ， 這就意味著帳戶上的數字在 $ 4 9 9～－ $ 500 之間。假設我們不會一次取出 $ 5 0 0，也不會寫一張超過 $ 5 0 0的支票，同時我們只處理美元，而不考慮到更小的貨幣單位—美分。

           這些假設表明帳戶能處理的數字範圍是從－ 5 0 0～4 9 9，總共 1 0 0 0個數。這個限制暗示我們只能用 3位十進位制數，且可不用負號來表示這 1 0 0 0個數。其中的關鍵在於我們不需要 5 0 0～9 9 9之間的正數，所以它們就可以用來表示負數。下面是其工作原理：

              換句話說，以 5、 6、 7、 8、 9開頭的 3位數實際上都表示負數。不用如下的表示法：

              而用這樣的表示法：   

              注意這樣形成了一個環形排序，最小的負數（ 5 0 0）看上去是最大的正數（ 4 9 9）的延續。數字9 9 9是比零小的第一個負數。如果給 9 9 9加上1 ，通常得到 1 0 0 0。但由於只處理 3 位數，所以實際上是 0 0 0。

              這種處理稱為1 0的補數 。要把 3位負數轉換成 1 0的補數，需從 9 9 9中減去它再加 1 。換句話說， 1 0的補數是 9的補數再加 1 。例如，要把－ 2 5 5寫成 1 0的補數，應先從 9 9 9中減去 2 5 5得到7 4 4，再加上 1 後得到 7 4 5。

              你可能聽說過“減法不過是負數的加法”，你也可能回答過“其實還是不得不做減法”。然而，通過使用 1 0的補數，就不用去做減法了，全部都可以用加法來計算。

              假設你有餘額為 $ 1 4 3的帳戶，並寫了一張 $ 7 8的支票，這表明你要把－ 7 8加到1 4 3上。－ 7 8的補數是 9 9 9－ 7 8 + 1 ，即 9 2 2。所以新的餘額是 1 4 3＋ 9 2 2（忽略上溢） ，即 6 5 。若我們再寫一張$ 1 5 0的支票，則必須減去 1 5 0，用補數表示就是 8 5 0。先前的餘額0 6 5加上8 5 0等於9 1 5，所以，新的餘額實際上是－ $ 8 5。

             二進位制中對應的系統稱為 2的補數 。假設我們用 8 位二進位制數工作，範圍從 0 0 0 0 0 0 0 0～11111111 ，對應於十進位制的 0～ 2 5 5。這時如果你想要表達負數，則以 1 開頭的每個 8位數都表示一個負數，如下所示：

             你可以表示的數的範圍從－ 1 2 8 ～1 2 7。最左邊的一位稱為符號位， 1 表示負數， 0表示正數。

            要計算2的補數得先求出 1 的補數再加上 1 ，這等同於先求反再加 1 。例如，十進位制數 1 2 5是0 11111 0 1 ，要用 2的補數來表示－ 1 2 5，可先取反得 1 0 0 0 0 0 1 0，再加 1 就得到 1 0 0 0 0 0 11 。可用上表來驗證這個結果。要回到原來的數只需同樣的操作：取反後加 1 。

            這個系統使不用負號就能表示正、負數，它也使我們只用加法規則就可以隨意進行正、負數運算。例如，計算－ 1 2 7 + 1 2 4，利用上表即得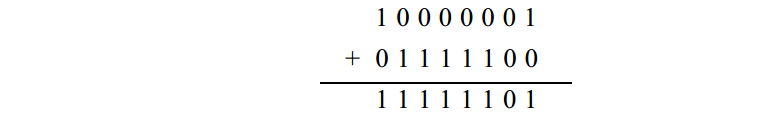
           

和是十進位制的－ 3。
           這裡要注意上溢或下溢，即結果大於 1 2 7或小於－ 1 2 8的情況。例如， 1 2 5加1 2 5：

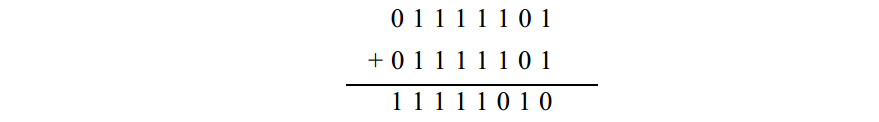
          因為最高位是１，結果代表一個負數：－ 6。再看－ 1 2 5加上它自已：

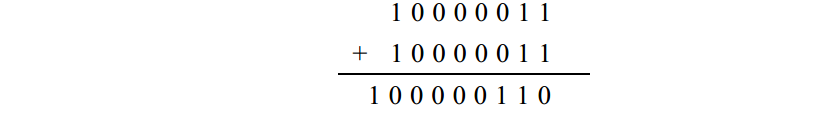
          由於限制了只取 8位數，所以最左邊的 1 被扔掉，剩下的 8位表示6。

          一般而言，若兩個運算元的符號相同，而結果的符號與運算元的符號不相同時，這樣的加法是無效的（即加法運算產生了溢位！）。

           現在，二進位制數可以有兩種不同的使用方法。二進位制數可以是無符號的或有符號的，無符號的二進位制 8位數的表示範圍從 0～ 2 5 5，有符號的二進位制 8位數的表示範圍從－ 1 2 8～ 1 2 7。這些數本身不會告訴你它們是否帶有符號。例如，假設有人問： “ 1 0 11 0 11 0對應於十進位制數的幾？”這時，你必須先問清楚它是無符號數還是有符號數？它可能是 1 8 2或－ 7 4。

           這就是二進位制數的麻煩：它們僅僅是一些 0和1 而沒有告訴它們的任何含義。