中心極限定理的形象理解
中心極限定理是統計學中的一個重要定理,本文的目的是形象地講解中心極限定理,不列舉公式。
本篇部落格是基於猴子在知乎上的回答,進行的整理。非常感謝猴子的講解。
目錄
1 什麼是中心極限定理
有時候統計概率就像魔術一樣,能夠從少量資料中得出不可思議的強大結論。我們只需要對1000個美國人進行電話調查,就能去預測美國總統大選的得票數。
通過對為肯德基提供雞肉的加工廠生產的100塊雞肉進行病毒(沙門氏菌)檢測,就能得出這家工廠的所有肉類產品是否安全的結論。
這些“一概而論”的強大能力,到底是從哪裡來的?
這背後的祕密武器就是統計概率的第2大護法:中心極限定理
1.1 簡單定義
中心極限定理是許多統計活動的“動力源泉”,這些活動存在著一個共同的特點,那就是使用樣本對總體進行估計,例如我們經常看到的民意調查就是這方面的經典案例。
那麼,什麼是中心極限定理呢?
中心極限定理是說:
1、樣本的平均值約等於總體的平均值。
2、不管總體是什麼分佈,任意一個總體的樣本平均值都會圍繞在總體的整體平均值周圍,並且呈正態分佈。
可能看了這兩句話,大家還是有些蒙。
彆著急,接下來,我將拆開這2句話來慢慢為你聊清楚什麼是中心極限定理。
假設有一個群體,如我們之前提到的清華畢業的人,我們對這類人群的收入感興趣。怎麼知道這群人的收入呢?我會做這樣4步:
第1步.隨機抽取1個樣本,求該樣本的平均值。例如我們抽取了100名畢業於清華的人,然後對這些人的收入求平均值。
該樣本里的100名清華的人,這裡的100就是該樣本的大小。
有一個經驗是,樣本大小必須達到30,中心極限定理才能保證成立。
第2步.我將第1步樣本抽取的工作重複再三,不斷地從畢業的人中隨機抽取100個人,例如我抽取了5個樣本,並計算出每個樣本的平均值,那麼5個樣本,就會有5個平均值。
這裡的5個樣本,就是指樣本數量是5,即抽取了5次,形成了5個樣本。
第3步.根據中心極限定理,這些樣本平均值中的絕大部分都極為接近總體的平均收入。有一些會稍高一點,有一些會稍低一點,只有極少數的樣本平均值大大高於或低於群體平均值。
第4步.中心極限定理告訴我們,不論所研究的群體是怎樣分佈的,這些樣本平均值會在總體平均值周圍呈現一個正態分佈。
1.2 形象演示
1.2.1 例子1
這裡給大家介紹一個演示中心極限定理的工具:演示中心極限定理。
下面我會介紹下這個演示程式,方便你最後可以自己動手親自操作。
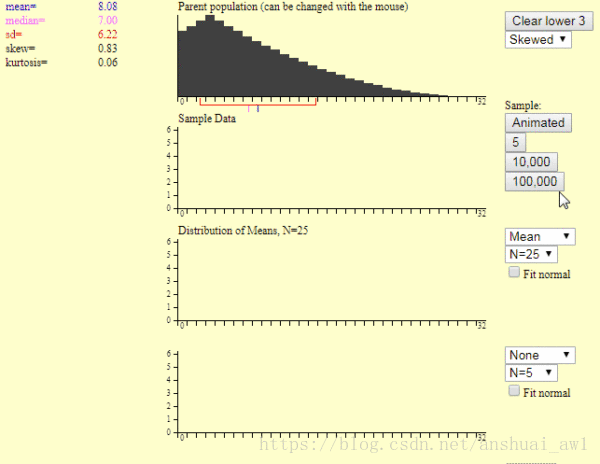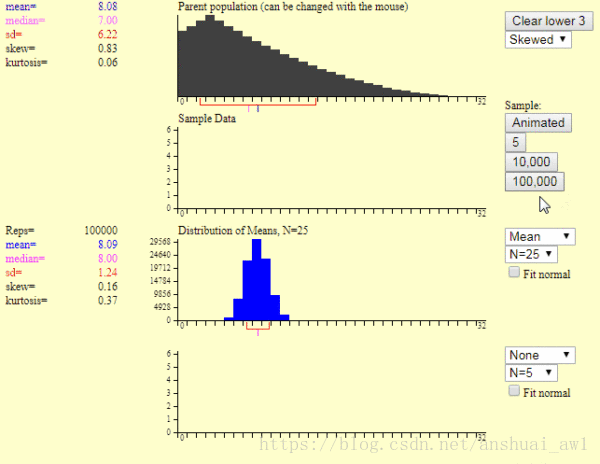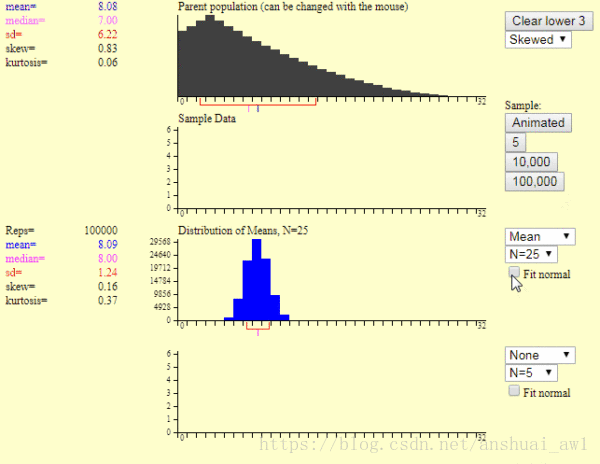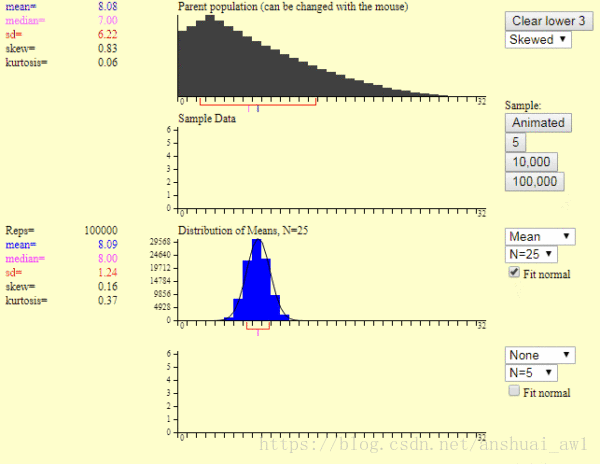
開啟這個程式以後,你會發現如下面圖片中所示的三個統計圖。
最上面的圖是總體分佈圖,左邊是一些統計指標,這裡我們只要關注總體平均值就可以了,通過選擇第1個圖中紅色箭頭表示的地方來改變總體的分佈,你可以選擇總體是正態分佈,或者非正態分佈。
第2個統計圖用來模擬產生一個樣本的過程。每點選1次紅色箭頭標識的地方,就生成一個樣本。這樣通過重複點選這個按鈕,你可以生成多個樣本。
這個按鈕下面的5,1千,1萬數字表示,你點選該按鈕,一次性幫你生成的樣本數量。
為了看清楚每個樣本產生的過程,建議一開始通過點選第2個圖中紅色箭頭那裡的按鈕來自己生成多個樣本。
第3個圖是,樣本均值分佈圖。右邊第一個你可以選擇統計指標,這裡我們選擇平均值就可以。
第2個N是表示樣本的大小,即一個樣本里面有多少個數據。這裡可供我們選擇的最大值是25。
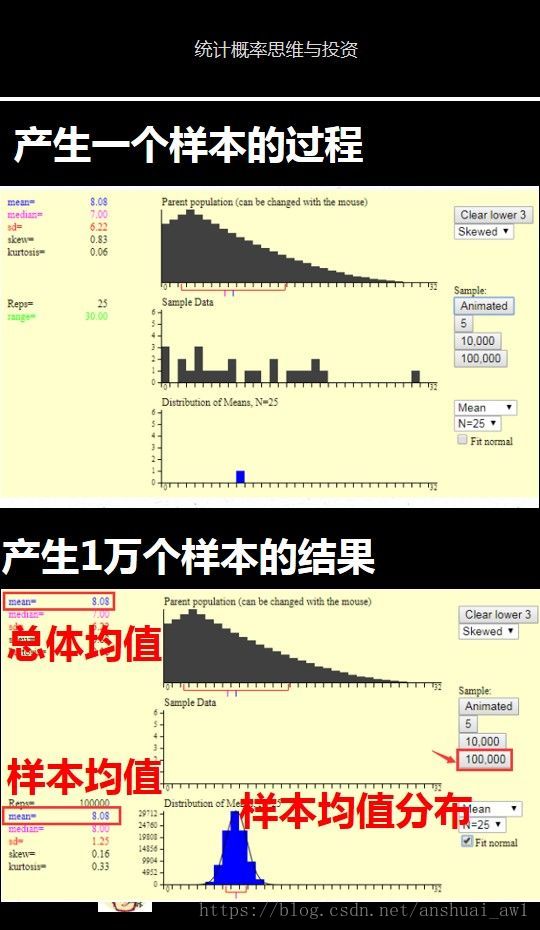
現在我點選第2個圖中紅色箭頭處的按鈕,便產生了下面圖片的樣本均值圖
這裡的第1個圖是產生一個樣本的過程,第2個圖是產生1萬個樣本的結果。我們可以發現:
1)樣本平均值約等於總體平均值。
2)不管總體是什麼分佈,任意一個樣本平均值都會圍繞在總體平均值周圍,並且呈正態分佈。
這就是中心極限定理,就是上述的這麼2句話。
1.2.2 例子2
下面圖片也可以完美的解釋中心極限定理。
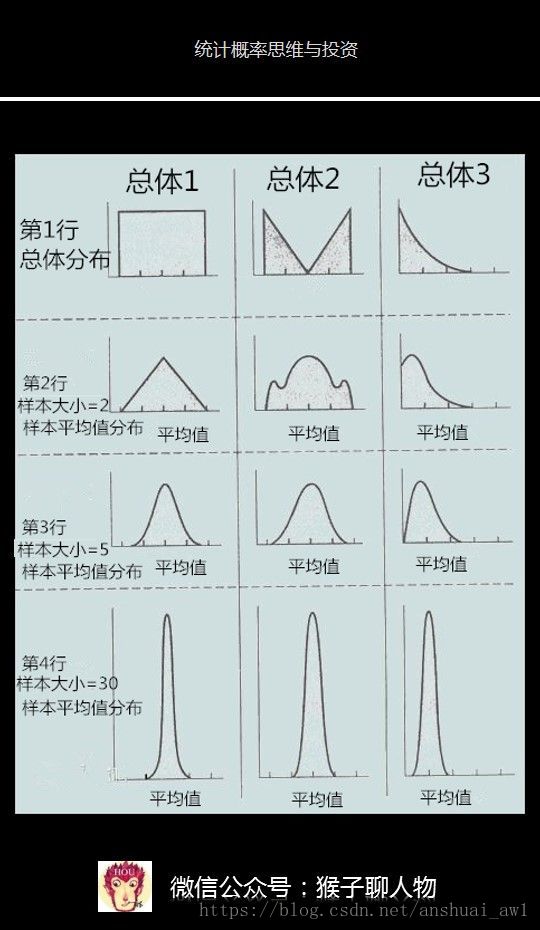
這裡第1行是3種不同分佈型別的總體,用於比較不同型別下的樣本平均值分佈。
第2行每個樣本大小是2,然後對每個樣本求平均值,橫軸表示每個樣本的平均值,縱軸表示該平均值出現了多少次,最後平均值分佈很不規則
第3行每個樣本大小是5,然後對每個樣本求平均值,最後平均值分佈有點接近於正態分佈,但是總體3對應的第3行卻不是正態分佈。
第4行每個樣本大小是30,然後對每個樣本求平均值,最後平均值分佈是正態分佈。
這也驗證了中心極限定律,不管總體是什麼分佈,任意一個總體的樣本平均值都會圍繞在總體的平均值周圍,並且呈正態分佈。
現在你已經知道了中心極限定理的大體意思,下面圖片我們通過幾個案例來實踐應用下。
2 中心極限定理應用案例
根據《2017年中國家庭財富調查報告》調查資料顯示,2016年我國家庭人均財富大約為16.9萬元(169077元)
(其中,房產淨值是家庭財富最重要的組成部分。在全國家庭的人均財富中,房產淨值的佔比為65.99%)
現在假設我們隨機抽樣1000箇中國家庭並詢問他們的年收入。
根據已知的這些資訊,從中心極限定理出發,你能得出什麼資訊?
下面我們一起來用中心極限定理進行推理。
1)根據中心極限定理,我們可以得出的第1個結論是:用樣本來估計總體。任何一個樣本的平均值將會約等於其所在總體的平均值。
例如你久居大城市,過年回老家,大街上遇到了鄰居大媽,雖然20年沒見你,鄰居大媽還是一眼認出你了,這不是隔壁老王家的孩子嘛,長的真帶勁。
這裡,你爸媽就是總體,你就是你爸媽的樣本,和你爸媽長的相似。
同樣的,一個正確抽取的家庭樣本應該能夠反映中國所有家庭的情況,裡面會包含收入高的公司高管,也會包括普通的員工,快遞小哥、警察以及其他人,這些人出現的頻率與他們在人口構成中的佔比相關。
因此,我們能夠推測,這個包含1000箇中國家庭代表性樣本的家庭財富的平均值約等於總體的平均值。
2) 樣本平均值呈正態分佈
在這個例子中,樣本平均值將會圍繞著群體平均值(也就是16.9萬元)形成一條正態分佈曲線。記住,群體本身的分佈形態並不重要,中國家庭收入的分佈曲線並非正態分佈,但樣本平均值的分佈曲線卻是正態分佈。
如果我們連續抽取100次包含1000個家庭的樣本,並將它們的平均值的出現頻率在座標軸上標出,那麼我們基本可以確定在總體平均值周圍將會呈現正態分佈。
取樣次數越多,結果就越接近正態分佈;而且樣本大小越大,分佈就越接近正態分佈。
3 如何用樣本估計總體
現在我們已經可以用樣本來估計出總體平均值。現在我想用樣本來估計出總體的標準差,該怎麼辦呢?
3.1 樣本標準差與總體標準差
我們已經知道,一個數據集的標準差是數值與平均值的偏離程度。
當你選擇一個樣本後,相比總體,你擁有資料的數量是變少了,因此,與總體中的數值偏離平均值的程度相比,樣本中很有可能把較為極端的數值排除在外,這樣使得數值更有可能以更緊密的方式聚集在均值周圍。
也就是說,樣本的標準差要小於總體標準差。
所以,為了更好的用樣本估計總體的標準差,統計學家就將標準差的公式做了像下面圖中公式中這樣的改造。
即原來的標準差公式是除以n,為了用樣本估計總體標準差,現在是除以n-1。這樣就是的標準略大。一般用字母s表示用樣本估計出的總體標準差。
很多書上都會把除以n-1的標準差叫做樣本標準差,其實會給很多人造成誤解。其實這個樣本標準差的目的是用於估計總體標準差。
你可能會疑惑,那我什麼時候標準差除以n還是n-1呢?
那就要看你使用標準差的目的是什麼。
如果你只是想計算一個數據集的標準差,那麼就除以n,例如你有100個畢業與清華人的收入,只是想了解這100個人構成的資料集的波動大小,那你就用除以n的標準差公式。
如果你想把這100個人當成一個樣本,用這個樣本來估計出總體(所有畢業與清華人的收入)的標準差,那麼就除以n-1的標準差公式。
3.2 標準誤差
我們再看下什麼是標準誤差?
標準差是用來衡量資料集的波動大小。比如畢業於清華大學所有人的收入分佈。
標準誤差其實也是標準差,只不過它是所有樣本平均值的標準差。
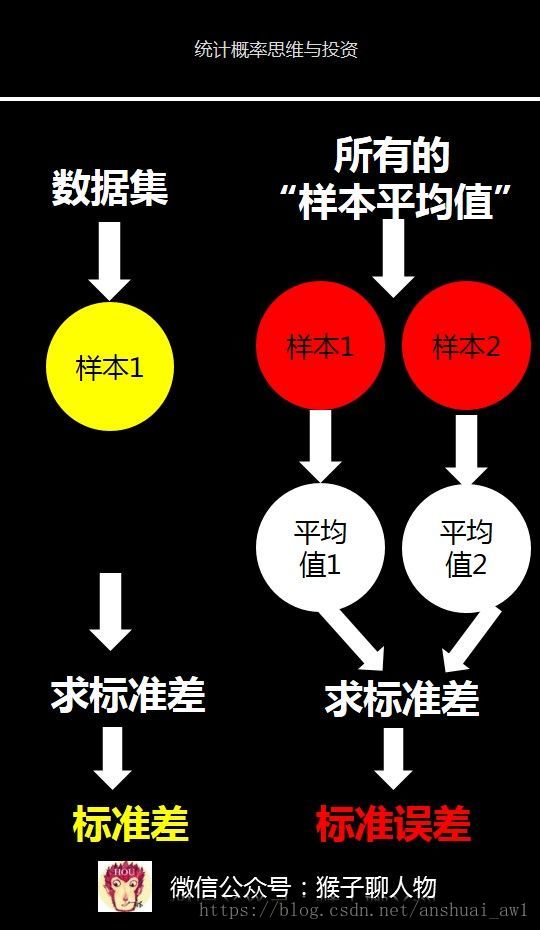
結合我下圖就更容易理解了。
如果我從畢業於清華大學中抽取100個人作為樣本1,然後我計算出標準差。那麼這個標準差就是用來描述這100個人組成的資料集的波動大小。
我連續剛才重複抽取樣本的動作,最後抽取出2個樣本,每個樣本都有100個人。對每個樣本計算平均值,這樣就有2個平均值。
這2個平均值其實組成了1個新的資料集,就是所有的“樣本平均值”。然後對這2個平均值資料計算出標準差。就是標準誤差。
你看,標準誤差其實也是標準差,只不過它的計算物件是所有的“樣本平均值”。所以,標準誤差是用來衡量樣本平均值的波動大小。
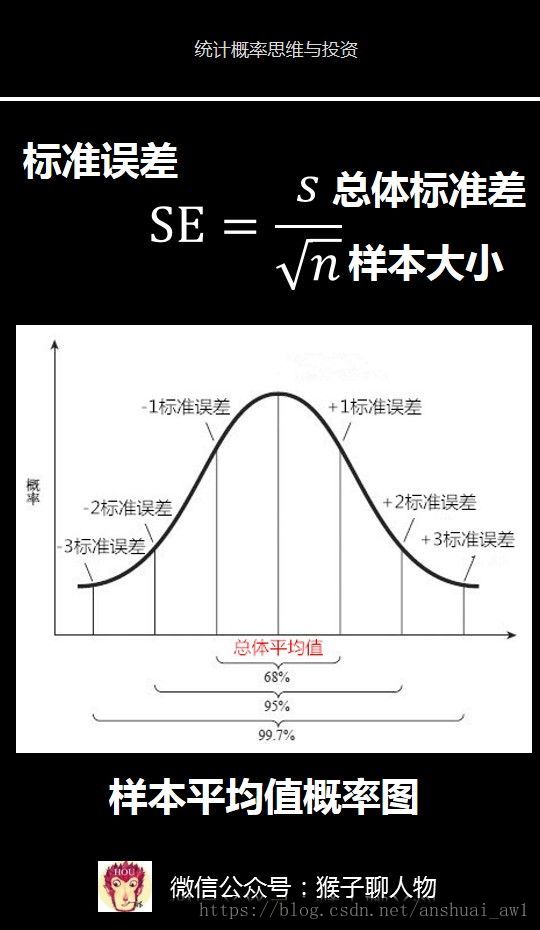
其實,計算標準誤差有個簡單的公式。下面圖片我們一起看下。
標準誤差SE等於總體標準差除以n的開方。但是我們不知道總體標準差怎麼辦。其實前面我們已經講了可以用樣本來估計出總體標準差的公式s。
根據中心極限定理,我們知道樣本平均值是呈正態分佈的,那麼我們便可以通過這裡圖片中的樣本平均值概率圖來獲得推理所需的“超能力”。
看到這個圖是不是很熟悉,這個圖其實就是正態分佈概率圖,只不過這裡的橫軸是樣本平均值的大小,縱軸是該平均值出現的概率。這裡是標準誤差。
在前面介紹正態分佈的時候,我們已經知道了正態分佈的一個奇特超能力,應用到樣本正態分佈上,那就是:
1)有68%的樣本平均值會在總體平均值一個標準誤差的範圍之內
數值範圍(總體平均值-1個標準誤差,總體平均值+1個標準誤差)
2)有95%的樣本平均值會在總體平均值的兩個標準誤差的範圍之內
(總體平均值-2個標準誤差,總體平均值+2個標準誤差)
3)有99.7%的樣本平均值會在總體平均值3個標準誤差的範圍之內。
(總體平均值-3個標準誤差,總體平均值+3個標準誤差)假如某個樣本的平均值減去總體的平均值,大於3個標準誤差。根據99.7%的樣本平均值會處於總體平均值3個標準誤差的範圍內,因此我們可以得出該樣本不屬於總體。
4 一句話總結中心極限定理
1. 中心極限定理也就是這麼兩句話:
1)任何一個樣本的平均值將會約等於其所在總體的平均值。
2)不管總體是什麼分佈,任意一個總體的樣本平均值都會圍繞在總體的平均值周圍,並且呈正態分佈。
2. 中心極限定理有什麼用呢?
1)在沒有辦法得到總體全部資料的情況下,我們可以用樣本來估計總體
如果我們掌握了某個正確抽取樣本的平均值和標準差,就能對估計出總體的平均值和標準差。
舉個例子,如果你是北京西城區的領導,想要對西城區裡的各個學校進行教學質量考核。
同時,你並不相信各個學校的的統考成績,因此就有必要對每所學校進行抽樣測試,也就是隨機抽取100名學生參加一場類似統考的測驗。
作為主管教育的領導,你覺得僅參考100名學生的成績就對整所學校的教學質量做出判斷是可行的嗎?
答案是可行的。中心極限定理告訴我們,一個正確抽取的樣本不會與其所代表的群體產生較大差異。也就是說,樣本結果(隨機抽取的100名學生的考試成績)能夠很好地體現整個群體的情況(某所學校全體學生的測試表現)。
當然,這也是民意測驗的執行機制所在。通過一套完善的樣本抽取方案所選取的1200名美國人能夠在很大程度上告訴我們整個國家的人民此刻正在想什麼。
2)根據總體的平均值和標準差,判斷某個樣本是否屬於總體
如果我們掌握了某個總體的具體資訊,以及某個樣本的資料,就能推理出該樣本是否就是該群體的樣本之一。
通過中心極限定理的正態分佈,我們就能計算出某個樣本屬於總體的概率是多少。如果概率非常低,那麼我們就能自信滿滿地說該樣本不屬於該群體。
這也是統計概率中假設檢驗的原理。