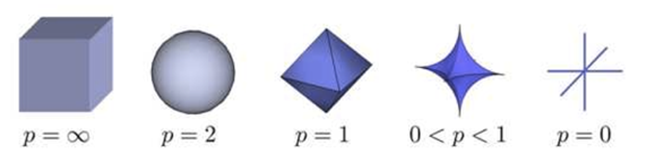機器學習中一個重要的話題便是模型的泛化能力，泛化能力強的模型才是好模型，對於訓練好的模型，若在訓練集表現差，不必說在測試集表現同樣會很差，這可能是欠擬合導致；若模型在訓練集表現非常好，卻在測試集上差強人意，則這便是過擬合導致的，過擬合與欠擬合也可以用 Bias 與 Variance 的角度來解釋，欠擬合會導致高 Bias ，過擬合會導致高 Variance ，所以模型需要在 Bias 與 Variance 之間做出一個權衡。

過擬合與欠擬合

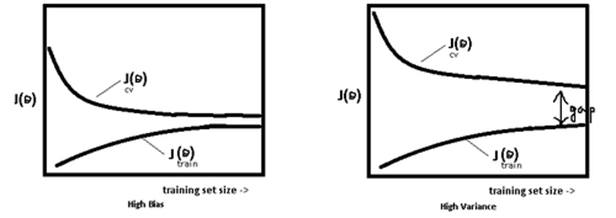
使用簡單的模型去擬合複雜資料時，會導致模型很難擬合數據的真實分佈，這時模型便欠擬合了，或者說有很大的 Bias，Bias 即為模型的期望輸出與其真實輸出之間的差異；有時為了得到比較精確的模型而過度擬合訓練資料，或者模型複雜度過高時，可能連訓練資料的噪音也擬合了，導致模型在訓練集上效果非常好，但泛化效能卻很差，這時模型便過擬合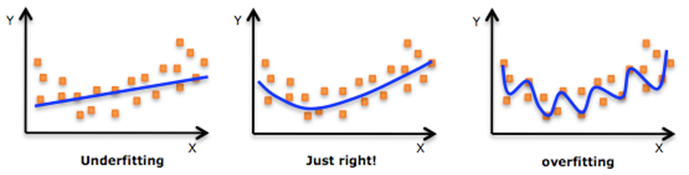

了，或者說有很大的 Variance，這時模型在不同訓練集上得到的模型波動比較大，Variance 刻畫了不同訓練集得到的模型的輸出與這些模型期望輸出的差異。模型處於過擬合還是欠擬合，可以通過畫出誤差趨勢圖來觀察。若模型在訓練集與測試集上誤差均很大，則說明模型的 Bias 很大，此時需要想辦法處理 under-fitting ；若是訓練誤差與測試誤差之間有個很大的 Gap ，則說明模型的 Variance 很大，這時需要想辦法處理 over-fitting。

一般在模型效果差的第一個想法是增多資料，其實增多資料並不一定會有更好的結果，因為欠擬合時增多資料往往導致效果更差，而過擬合時增多資料會導致 Gap 的減小，效果不會好太多，多以當模型效果很差時，應該檢查模型是否處於欠擬合或者過擬合的狀態，而不要一味的增多資料量，關於過擬合與欠擬合，這裡給出幾個解決方法。

解決欠擬合的方法：

• 增加新特徵，可以考慮加入進特徵組合、高次特徵，來增大假設空間;
• 嘗試非線性模型，比如核SVM 、決策樹、DNN等模型;
• 如果有正則項可以較小正則項引數 λλ.
• Boosting ,Boosting 往往會有較小的 Bias，比如 Gradient Boosting 等.

解決過擬合的方法：

• 交叉檢驗，通過交叉檢驗得到較優的模型引數；
• 特徵選擇，減少特徵數或使用較少的特徵組合，對於按區間離散化的特徵，增大劃分的區間。
• 正則化，常用的有 L1L1、L2L2 正則。而且 L1L1 正則還可以自動進行特徵選擇。
• 如果有正則項則可以考慮增大正則項引數 λλ.
• 增加訓練資料可以有限的避免過擬合.
• Bagging ,將多個弱學習器Bagging 一下效果會好很多，比如隨機森林等；

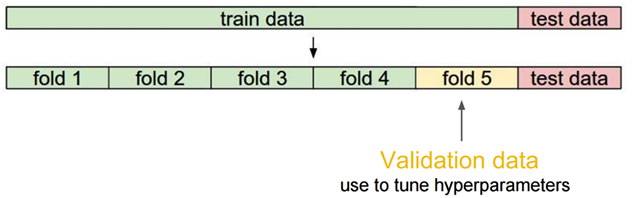
交叉檢驗

當資料比較少是，留出一部分做交叉檢驗可能比較奢侈，還有隻執行一次訓練-測試來評估模型，會帶有一些隨機性，這些缺點都可以通過交叉檢驗克服，交叉檢驗對資料的劃分如下：

交叉檢驗的步驟：

1）將資料分類訓練集、驗證集、測試集；

2）選擇模型和訓練引數；

3）使用訓練集訓練模型，在驗證集中評估模型；

4）針對不同的模型，重複2）- 3）的過程；

5）選擇最佳模型，使用訓練集和驗證集一起訓練模型；

6）使用測試集來最終測評模型。

關於正則

在模型的損失函式中引入正則項，可用來防止過擬合，於是得到的優化形式如下：

w∗=argminwL(y,f(w,x))+λΩ(w)w∗=argminwL(y,f(w,x))+λΩ(w)

這裡 Ω(w)Ω(w) 即為正則項， λλ  則為正則項的引數，通常為 LpLp 的形式，即：

Ω(w)=||w||pΩ(w)=||w||p

實際應用中比較多的是 L1L1 與 L2L2 正則，L1L1 正則是 L0L0 正則的凸近似，這裡 L0L0 正則即為權重引數 ww 中值為 0 的個數，但是求解 L0L0 正則是個NP 難題，所以往往使用 L1L1 正則來近似 L0L0 , 來使得某些特徵權重為 0 ，這樣便得到了稀疏的的權重引數 ww。關於正則為什麼可以防止過擬合，給出三種解釋：

正則化的直觀解釋

對於規模龐大的特徵集，重要的特徵可能並不多，所以需要減少無關特徵的影響，減少後的模型也會有更強的可解釋性；L2L2 正則可以用來減小權重引數的值，當權重引數取值很大時，導致其導數或者說斜率也會很大，斜率偏大會使模型在較小的區間裡產生較大的波動。加入L2L2 正則後，可使得到的模型更平滑，比如說下圖所示曲線擬合，展示了加入L2L2 正則與不加 L2L2 的區別：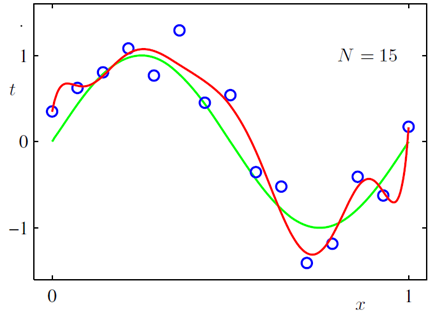

正則化的幾何解釋

我們常見的正則，是直接加入到損失函式中的形式，其實關於 L1 與 L2 正則，都可以形式化為以下問題：

L1:minwL(y,f(w,x))    L2:minwL(y,f(w,x))    s.t.||w||22<Cs.t.||w||11<CL1:minwL(y,f(w,x))    s.t.||w||22<CL2:minwL(y,f(w,x))    s.t.||w||11<C

至於兩種形式為什麼等價呢，運用一下拉格朗日乘子法就好，這裡也即通常說的把 ww 限制在一個ball 裡，對於 lp–balllp–ball 的形式如下圖所示：  

對於 L1L1 與 L2L2 正則，分別對應l1–balll1–ball 與 l2–balll2–ball ，為了方便看，這裡給出 l1–balll1–ball 與 l2–balll2–ball 在二維空間下的圖：

l1−ball:l2−ball: |w1|+|w2|<C w21+w22<Cl1−ball: |w1|+|w2|<Cl2−ball: w12+w22<C

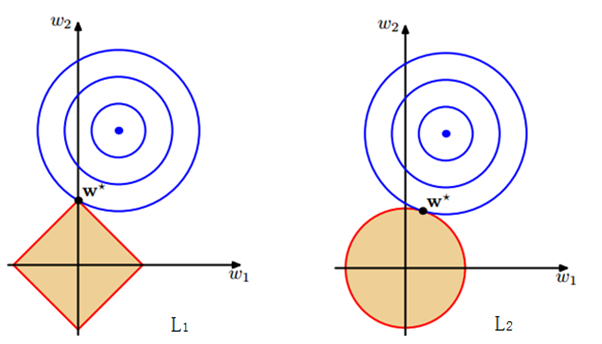
下圖中的等高線即為模型的損失函式，上式中的兩個約束條件則變成了一個半徑為 CC 的 norm-ball 的形式，等高線與 norm-ball 相交的地方即為最優解：

可以看到，l1−balll1−ball 和每個座標軸相交的地方都有“角”出現，而目標函式除非位置非常好，大部分時候都會在角的地方相交。注意到在角的位置即導致某個維度為 0 ，這時會導致模型引數的稀疏，這個結論可自然而然的推廣到高維的情形；相比之下，l2−balll2−ball 就沒有這樣的性質，因為沒有角，所以第一次相交的地方出現在具有稀疏性的位置的概率就變得非常小了。

正則化的貝葉斯解釋

正則化的另一種解釋來自貝葉斯學派，在這裡可以考慮使用極大似然估計 MLE 的方式來當做損失函式，對於 MLE 中的引數 ww ，為其引入引數為 αα  的先驗，然後極大化 likelihood ×× prior，便得到了 MLE 的後驗估計 MAP 的形式：

MLE:MAP:L(w)=p(y|x,w)L(w)=p(y|x,w)p(w|α)MLE:L(w)=p(y|x,w)MAP:L(w)=p(y|x,w)p(w|α)

對於 L2L2 正則，是引入了一個服從高斯分佈的先驗，而對於 L1L1  正則，是引入一個拉普拉斯分佈的先驗，兩個分佈分別如下：

Gussian:Laplace:p(x,μ,σ)=12π‾‾‾√σexp(−(x−μ)22σ2)p(x,μ,b)=12bexp(−|x−μ|b)Gussian:p(x,μ,σ)=12πσexp(−(x−μ)22σ2)Laplace:p(x,μ,b)=12bexp(−|x−μ|b)

兩種分佈的概率密度的圖形如下所示：

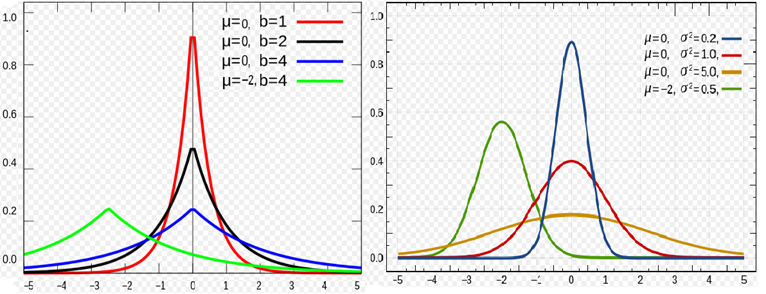
下面為引數 ww 引入一個高斯先驗，即 w∼(0,α−1I)w∼N(0,α−1I)：

p(w|α)=(w|0,α−1I)=(α2π)n/2exp(−α2wTw)p(w|α)=N(w|0,α−1I)=(α2π)n/2exp⁡(−α2wTw)

這裡的 nn 即為引數 ww 的維度，所以得到其 MAP 形式為：

L(w⃗ )=p(y⃗ |X;w)p(w⃗ )=∏i=1mp(y(i)|x(i);w)p(w|0,a−1I)=∏i=1m12π‾‾‾√δexp(−(y(i)−wTx(i))22δ2)likelihoodα2πn/2exp(−wTw2α)priorL(w→)=p(y→|X;w)p(w→)=∏i=1mp(y(i)|x(i);w)p(w|0,a−1I)=∏i=1m12πδexp⁡(−(y(i)−wTx(i))22δ2)⏟likelihoodα2πn/2exp⁡(−wTw2α)⏟prior

其 loglog 似然的形式為：

logL(w)⇒=mlog12π‾‾‾√δ+n2loga2π−1δ2⋅12∑i=1m(y(i)−wTx(i))2−1α⋅12wTwwMAP=argminw(1δ2⋅12∑i=1m(y(i)−wTx(i))2+1α⋅12wTw)log⁡L(w)=mlog⁡12πδ+n2log⁡a2π−1δ2⋅12∑i=1m(y(i)−wTx(i))2−1α⋅12wTw⇒wMAP=arg⁡minw(1δ2⋅12∑i=1m(y(i)−wTx(i))2+1α⋅12wTw)

這便等價於常見的 MAP 形式：

J(w)=1N∑i(y(i)−wTx(i))2+λ||w||2J(w)=1N∑i(y(i)−wTx(i))2+λ||w||2

同理可以得到引入拉普拉斯的先驗的形式便為 L1L1 正則.具體的計算可見參考文獻88。

L1 產生稀疏解的數學解釋

對於樣本集合 {(xi,yi)}ni=1{(xi,yi)}i=1n， 其中 xi∈ℝpxi∈Rp ,換成矩陣的表示方法：

X⋅w=yX⋅w=y

上式的含義即為求解引數 ww ,當  p>np>n 時即資料量非常少，特徵非常多的情況下，會導致求解不唯一性，加上 L1L1 約束項可以得到一個確定的解，同時也導致了稀疏性的產生, L1L1 正則的形式如下：

L(w)=f(w)+λ||w||1L(w)=f(w)+λ||w||1

這裡損失函式採用了均方誤差損失，即:

f(w)=||X⋅w−y||2f(w)=||X⋅w−y||2

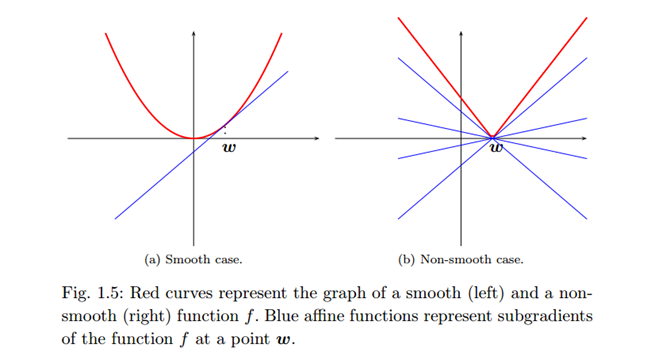
有唯一解的 L1L1 正則是一個凸優化問題，但是有一點，是不光滑的凸優化問題，因為在尖點處的導數是不存在的，因此需要一個 subgradient 的概念：

對於在 pp 維歐式空間中的凸開子集 UU 上定義任意的實值函式 f:U→ℝf:U→R , 函式 ff  在點 w0∈Uw0∈U 處的 subgradient 滿足:

f(w)–f(w0)≥g⋅(w–w0)f(w)–f(w0)≥g⋅(w–w0)

gg 構成的集合即為再點 w0w0 處的 subgradient 集合，如下圖右的藍色線所示：

比如說對於一維情況，f(w)=|w|f(w)=|w| ,該函式在 0 點不可導，用 subgradient 可以將其導數表示為：

f′(w)=⎧⎩⎨⎪⎪{1},     [−1,1],  {−1},   if w>0if w=0if w<0f′(w)={{1},     if w>0[−1,1],  if w=0{−1},   if w<0

接下來對損失函式求導即可：

∇wjL(w)=ajwj−cj+λ⋅sign(wj)where:           aj=2∑i=1nx2ij           cj=2∑i=1nxij(yi−wT¬jxi¬j)∇wjL(w)=ajwj−cj+λ⋅sign(wj)where:           aj=2∑i=1nxij2           cj=2∑i=1nxij(yi−w¬jTxi¬j)

因為 L1L1 正則的形式是根據拉格朗日乘子法得到的，拉格朗日法則需要滿足 KKT 條件，即 ∇wjL(w)=0∇wjL(w)=0 ,因此另導數得 0 ，並且使用 subgradient 的概念，可以得到 wjwj 在尖點的導數取值範圍：

∇wjL(w)=ajwj−cj+λ⋅sign(wj)=0∇wjL(w)=ajwj−cj+λ⋅sign(wj)=0

利用 可得如下的形式：

ajwj−cj∈⎧⎩⎨⎪⎪{λ}, if wj<0[−λ,λ], if wj=0{−λ}, if wj>0ajwj−cj∈{{λ}, if wj<0[−λ,λ], if wj=0{−λ}, if wj>0

分幾下幾種情況：

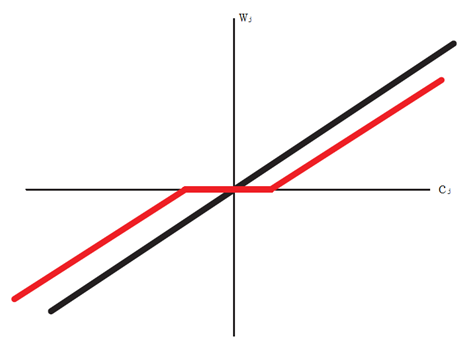
1)  若 cj<−λcj<−λ ,則 cjcj 與殘差負相關，這時的 subgradient 為 0即： ŵ j=cj+λaj<0w^j=cj+λaj<0

2)  若 cj∈[−λ,+λ]cj∈[−λ,+λ]，此時與殘差弱相關，且得到的 ŵ j=0w^j=0

3)  若 cj>λcj>λ, 此時 cjcj 與殘差正相關， 且有ŵ j=cj–λaj>0w^j=cj–λaj>0 

綜上可得：

ŵ j=⎧⎩⎨⎪⎪(cj+λ)/aj,  0       ,  (cj−λ)/aj,  if cj<−λif cj∈[−λ,λ]if cj>λw^j={(cj+λ)/aj,  if cj<−λ0       ,  if cj∈[−λ,λ](cj−λ)/aj,  if cj>λ

可見 cjcj 的取值正是導致稀疏性的由來，下圖可以見到 cjcj 與 wjwj 的關係：