在數學上，我們將滿足以下性質的數學模型的物理現象：

1. 解存在
2. 解唯一
3. 解連續依賴於初始邊界條件（the solution’s behavior changes continuously with the initial conditions）

稱適定問題。只要其中一個條件不滿足，則稱為不適定問題[1]

在數學、統計和電腦科學尤其是在機器學習和反演問題中，正則化通過引入額外的資訊去解決不適定問題或者防止過擬合。

Tikhonov Regularization

Tikhonov正則化方法由Andrey Tikhonov命名，最常用來進行不適定問題的正則化。在統計學中，這種方法稱為“嶺迴歸”，在機器學習領域，被稱為“weight decay”。在更多的獨立研究中，同樣稱為Tikhonov-Miller方法、Phillips-Twomey方法、約束線性反演方法和線性正則化方法。Tikhonov正則化方法與非線性最小二乘問題的Levenberg-marquardt演算法緊密相關的。

假設一個已知的矩陣A和向量b，我們希望求得一個向量x，如下表示：

Ax=b

求解x的標準方法為線性迴歸經典最小二乘。但是，如果沒有x滿足該等式或者不止一組x滿足，這就意味著解不唯一，即該問題稱為不適定問題（ill-posed problems）。像這樣的案例中，經典最小二乘估計值會導致過擬合或者獲得方程的欠定解。很多的現實世界中的現象都具有正向低通濾波的效果，其中x通過A對映到b。因此，在求解反演問題時，反演問題的解決方法就存在類似高通濾波器放大噪聲的趨勢（特徵值/奇異值在反向對映中值很大而在正向對映中值很小）。經典最小二乘的方法的基本原理是：殘差平方和最小，因此可表示為如下形式：

為了獲得具有理想性質的特解，可以在此最小化中包含了正則化項：

在很多的案例中，直接將Tikhonov矩陣Γ作為一個確定的矩陣（Γ=αI），這可以獲得一個較小的範數解，這是著名的L2正則化。這種正則化改進了問題的條件，從而獲得直接的數值解。這種解的顯示錶達為：

這種正則化的結果最終受到矩陣Γ的影響。如果矩陣Γ=0的話，上述的正則化解就是經典最小二乘的解。

L2正則化方法除了線上性迴歸中使用外，也被應用與其他的領域：基於邏輯迴歸或支援向量機的分類和矩陣分解中。

Generalized Tikhonov regularization

對於x和資料誤差的多元正態分佈，可以通過應用變數轉化使誤差減小。同樣地，可以獲得以下x的最小目標方程：

其中，

       這種廣義問題的最優化解可以顯示地表示為：

或者等價為：

Relation to singular-value decomposition and Wiener filter

       當Γ=αI時，可以使用奇異值分解對最小二乘解進行分析。則Tikhonov正則化解可以奇異值分解為以下形式：

其中，D是一個對角陣：

最後，其維納濾波器（Wiener Filter）的相關表示式為：

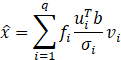
其中，表示為維納權重，q為A矩陣的秩。

Determination of the Tikhonov factor

正則化引數a通常是未知的，經常需要根據實際問題使用特殊的方法進行確定。一種可能的方法依賴於下面描繪的貝葉斯解釋（Bayesian interpretation）。其他的方法包含：偏差原理（discrepancy Principle）、交叉驗證（cross-validation）、L曲線法（L_Curve Method）、限制性最大似然估計（restricted maximum likelihood）和無偏預測風險估計（Unbiased predictive risk estimator）。Grace Wahba證明了這種最優引數，去一法交叉驗證最小（leave-one-out cross-validation）：

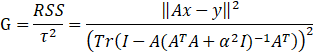
其中RSS表示殘差平方和，t表示自由度。

       使用之前的SVD方法，我們可以講話上述的表示式：

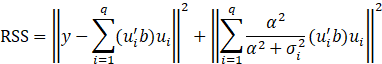
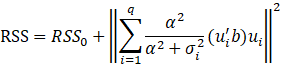
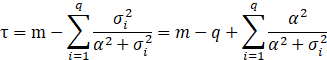
文章 參考：