1. 子序列

　　摘自維基百科

　　在數學中，某個序列的子序列是從最初序列通過去除某些元素但不破壞餘下元素的相對位置而形成的新序列。

例如：

令  為一序列

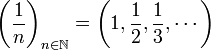
那麼，以下序列

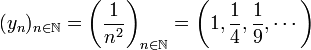
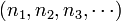是  的子序列之一。對應定義裡的自然數子序列  為 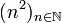，而所對應的對映函式為 。

　　2.　最長公共子序列

　　最長公共子序列問題是尋找兩個或多個已知數列最長的子序列

　　3. 解題思路

最長公共子序列的性質：

設序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}的最長公共子序列為Z={z1,z2,…,zk} ，則

　　(1)若xm=yn，則zk=xm=yn，且{z1...zk-1}是{x1...xm-1}和{y1...yn-1 }的最長公共子序列。

　　(2)若xm≠yn且zk≠xm，則{z1....zk } 是{x1...xm-1}和{y1....yn}最長公共子序列。

　　(3)若xm≠yn且zk≠yn，則{z1...zk}是{x1...xm}和{y1...yn-1}的最長公共子序列。

　　則可以有如下的遞迴關係：

　　c[i][j]表示x的第i位和y的第j位之前（包括i和j）的最長公共子序列的個數

因此在求解的時候也分為這三種情況來考慮即可。

　　4. 程式碼

//LCS  longest common subsequence

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAX 100

void LCS(char *x, char *y,int x_len, int y_len, int common_len[][MAX], int b[][MAX])
{
    //common_len[i][j]儲存的是x的第i位與有的第j位的公共子序列的長度
    //b[i][j] 記錄獲得common_len[i][j]的路徑：分別為0 -1 1，便於回溯輸出公共子串

    int i,j;
    
    for (i = 0; i < x_len; i++)
        common_len[i][0] = 0;
    for (j = 0; j < y_len; j++)
        common_len[0][j] =0;

    for (i = 1; i <= x_len; i++)
    {
        for (j = 1; j <= y_len; j++)
        {
            if (x[i-1] == y[j-1])  //從零開始儲存，所以第i位為x[i-1]
            {
                common_len[i][j] = common_len[i-1][j-1] + 1;
                b[i][j] = 0;
            }
            else if (common_len[i-1][j] >= common_len[i][j-1])
            {
                common_len[i][j] = common_len[i-1][j];
                b[i][j] = -1;
            }
            else
            {
                common_len[i][j] = common_len[i][j-1];
                b[i][j] = 1;
            }
        }
    }
}

void backtrack(int i, int j,int b[][MAX], char *x)
{
    if (0 == i || 0 == j) 
        return;
    else if (0 == b[i][j])
    {
        backtrack(i-1,j-1,b,x);
        printf("%c",x[i-1]);
    }
    else if(-1 == b[i][j])
    {
        backtrack(i-1,j,b,x);
    }
    else
    {
        backtrack(i,j-1,b,x);
    }
}

int main()
{
    int x_len,y_len;
    char x[MAX] = "ABCBDAB";
    char y[MAX] = "BDCABA";
    int common_len[MAX][MAX];
    int b[MAX][MAX];

    x_len = strlen(x);
    y_len = strlen(y);

    LCS(x,y,x_len,y_len,common_len,b);
    backtrack(x_len,y_len,b,x);
    
    printf("\n");
    
    
    return 0;
}

2013/8/8 11:27