二叉樹的遍歷基本操作
阿新 • • 發佈:2018-12-25
樹
一、樹的儲存方式
1、雙親表示法:用指標表示出每個節點的雙親(和自己的資料):根節點沒有雙親,其他的節點都有自己的雙親)
2、孩子表示法:用指標指出每棵樹的孩子節點,每個節點給出3個欄位(資料,兩棵子樹)【節點欄位為樹的度加1】
3、雙親孩子表示法:將孩子表示法和雙親表示法結合在一起
4、孩子兄弟表示法:既表示出每一個節點第一個孩子節點,也表示出每個節點的下一個兄弟節點
二、二叉樹(每個節點只有兩個分支):根節點加上左子樹、和右子樹構成的。
1、二叉樹也可能為空樹,是一個有序樹
2、特點:
(1)每個節點最多有兩棵子樹,即二叉樹不存在度大於2的節點
(2)二叉樹的子樹有左右之分,其子樹的次序不能顛倒
3、分類:
滿二叉樹:節點個數為2^n-1
完全二叉樹:(完全二叉樹,有n個節點,求其高度,當成滿二叉樹的格式來求:lgn
:單支樹浪費空間多,完全二叉樹沒有任何浪費
.h
#pragma once # include<stdio.h> # include<stdlib.h> # include<string.h> # include<malloc.h> # include<assert.h> typedef char DataType; typedef struct BinTreeNode{ struct BinTreeNode *_pLeft;//當前節點的左孩子 struct BinTreeNode *_pRight;//當前節點的右孩子 DataType _data;//節點裡面數據的型別 }Node, *PNode; void CreateBinTree(PNode *pRoot, DataType array[], int size, DataType invalid); void _CreateBinTree(PNode *pRoot, DataType array[], int size, int *index, DataType invalid); PNode BuyBinTreeNode(DataType data); PNode CopyBinTree(PNode pRoot); void PreOrder(PNode pRoot); void InOrer(PNode pRoot); void PostOrder(PNode pRoot); void DestroyBinTree(PNode *pRoot); //二叉樹的其他操作//求二叉樹節點的個數 int BinTreeSize(PNode pRoot); //求二叉樹葉子節點的個數 int BinTreeLeaf(PNode pRoot); //求二叉樹第k層節點的個數 int BinTreekLevelNode(PNode pRoot, int k); //求二叉樹的高度 int BinTreeHeight(PNode pRoot); //判斷一個節點是否在一棵二叉樹中 int IsNodeInBinTree(PNode pRoot, PNode Node); //找節點 PNode Find(PNode pRoot, DataType data);
.c
# include"tree.h" void CreateBinTree(PNode *pRoot, DataType array[], int size, DataType invalid){ int index = 0; _CreateBinTree(pRoot, array, size, &index, invalid); } void _CreateBinTree(PNode *pRoot, DataType array[], int size, int *index, DataType invalid){ assert(pRoot); assert(index); if (*index < size&&array[*index] != invalid){ *pRoot = BuyBinTreeNode(array[*index]); //建立根節點的左子樹 ++(*index); _CreateBinTree(&(*pRoot)->_pLeft, array, size, index, invalid); //建立右子樹 _CreateBinTree(&(*pRoot)->_pRight, array, size, index, invalid); } } PNode BuyBinTreeNode(DataType data){ PNode pNewNode = (PNode)malloc(sizeof(Node)); if (NULL == pNewNode) { assert(0); return; } pNewNode->_data = data; pNewNode->_pLeft = NULL; pNewNode->_pRight = NULL; return pNewNode; } PNode CopyBinTree(PNode pRoot){ PNode pNewRoot = NULL; //過濾空 if (pRoot) //拷貝根節點 { pNewRoot = BuyBinTreeNode(pRoot->_data); if (pRoot->_pLeft) //拷貝左子樹 pNewRoot->_pLeft = CopyBinTree(pRoot->_pLeft); if (pRoot->_pRight) //拷貝右子樹 pNewRoot->_pRight = CopyBinTree(pRoot->_pRight); return pNewRoot; } void PreOrder(PNode pRoot){ //前序遍歷(根,左,右) if (pRoot) { printf("%c ", pRoot->_data); PreOrder(pRoot->_pLeft); PreOrder(pRoot->_pRight); } } void InOrer(PNode pRoot){ //中序遍歷(左,根,右) if (pRoot) { InOrer(pRoot->_pLeft); printf("%c ", pRoot->_data); InOrer(pRoot->_pRight); } } void PostOrder(PNode pRoot){ //後序遍歷(左,右,根) if (pRoot) { PostOrder(pRoot->_pLeft); PostOrder(pRoot->_pRight); printf("%c ", pRoot->_data); } } void DestroyBinTree(PNode *pRoot){ assert(pRoot); if (*pRoot) { //先銷燬左子樹 DestroyBinTree(&(*pRoot)->_pLeft); //銷燬右子樹 DestroyBinTree(&(*pRoot)->_pRight); //銷燬根節點 free(*pRoot); *pRoot = NULL; } } //求二叉樹節點總個數 int BinTreeSize(PNode pRoot){ if (NULL == pRoot) return 0; int left = BinTreeSize(pRoot->_pLeft); int right = BinTreeSize(pRoot->_pRight); return left + right + 1; } //求二叉樹葉子節點的個數 int BinTreeLeaf(PNode pRoot){ if (NULL == pRoot) return 0; //不用遞迴到空的那一次 if ((NULL == pRoot->_pLeft) && (NULL == pRoot->_pRight)) return 1; return BinTreeLeaf(pRoot->_pLeft) + BinTreeLeaf(pRoot->_pRight); } //求二叉樹第k層節點的個數 int BinTreekLevelNode(PNode pRoot, int k){ if (NULL == pRoot || k <= 0) return 0; if (1 == k) return 1; return BinTreekLevelNode(pRoot->_pLeft, k - 1) + BinTreekLevelNode(pRoot->_pRight, k - 1); } 求二叉樹的高度 int BinTreeHeight(PNode pRoot){ int left = 0; int right = 0; if (NULL == pRoot) return 0; if (NULL == pRoot->_pLeft&&NULL == pRoot->_pRight) return 1; left = BinTreeHeight(pRoot->_pLeft); right = BinTreeHeight(pRoot->_pRight); return left > right ? (left + 1) : (right + 1); } int IsNodeInBinTree(PNode pRoot, PNode Node){ if (NULL == pRoot || NULL == Node) return 0; if (pRoot == Node) return 1; if (IsNodeInBinTree(pRoot->_pLeft, Node)) return 1; return IsNodeInBinTree(pRoot->_pRight, Node); } PNode Find(PNode pRoot, DataType data){ PNode Node = NULL; if (NULL == pRoot) return NULL; if (data == pRoot->_data) return pRoot; if (Node == Find(pRoot->_pLeft, data)) return Node; return Find(pRoot->_pRight, data); }
test.c
# include"Tree.h"
void Test1(){
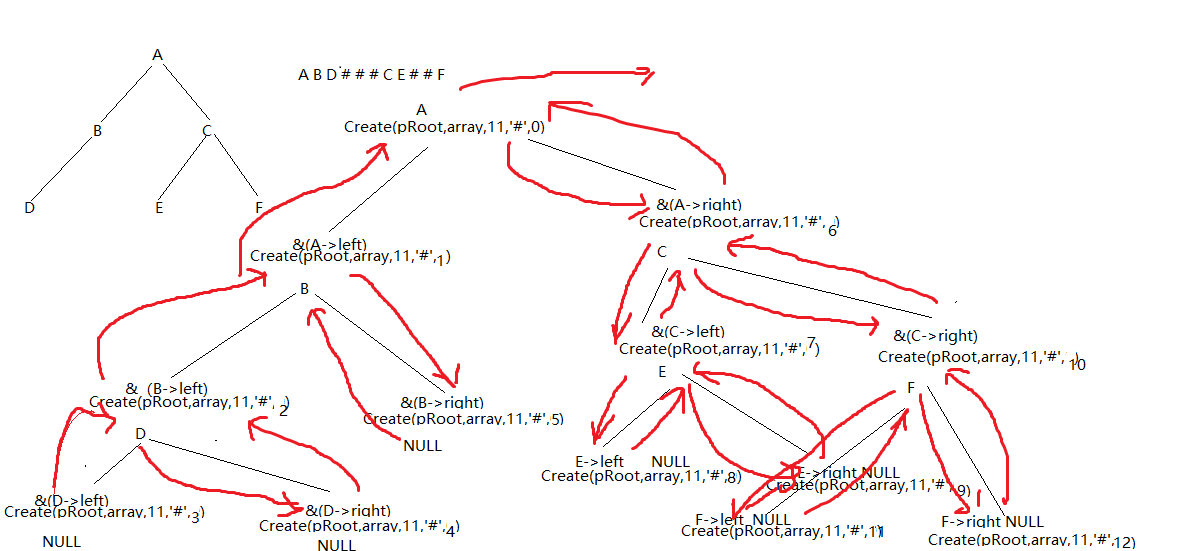
char *arr = "ABD###CE##F";
PNode pRoot = NULL;
PNode pNewRoot = NULL;
int len = strlen(arr);
CreateBinTree(&pRoot, arr, len, '#');
pNewRoot = CopyBinTree(pRoot);
PreOrder(pRoot);
PreOrder(pNewRoot);
}
void Test2(){
char arr[] = "ABD###CE##F";
PNode pRoot = NULL;
PNode pNewRoot = NULL;
int len = strlen(arr);
CreateBinTree(&pRoot, arr, len, '#');
pNewRoot = CopyBinTree(pRoot);
InOrer(pRoot); InOrer(pNewRoot);
}
void Test3(){
char arr[] = "ABD###CE##F";
PNode pRoot = NULL;
PNode pNewRoot = NULL;
int len = strlen(arr);
CreateBinTree(&pRoot, arr, len, '#');
pNewRoot = CopyBinTree(pRoot);
PostOrder(pRoot);
PostOrder(pNewRoot);
}
void test4(){
PNode pRoot = NULL;
PNode Node = Find(PreOrder, 'E');
if (IsNodeInBinTree(pRoot, Node))
printf("在");
else printf("不在");
}int main(){
//Test1();
//Test2();
Test3();
system("pause");
return 0;
}
結果: