圖、圖的儲存、圖的遍歷
圖(Graph)是由頂點的有窮非空集合和頂點之間的邊組成。G(V,E) V表示頂點的集合,E表示邊的集合。
在無向圖中,邊可以表示為E1={(A,D),(B,C)}
在有向圖中,頂點v1和v2的有向邊稱為弧。表示為<v1,v2> v1稱為弧尾,v2稱為弧頂。
在無向圖中,如果任意邊兩個頂點都存在邊,則該圖為無向完全圖,n個頂點的無向完全圖有n*(n-1)/2條邊。
在有向圖中,如果任意邊兩個頂點都存在互為相反邊,則該圖為有向完全圖,n個頂點的有向完全圖有n*(n-1)條邊。
稀疏圖,稠密圖。
帶權圖稱為網。
子圖如下。
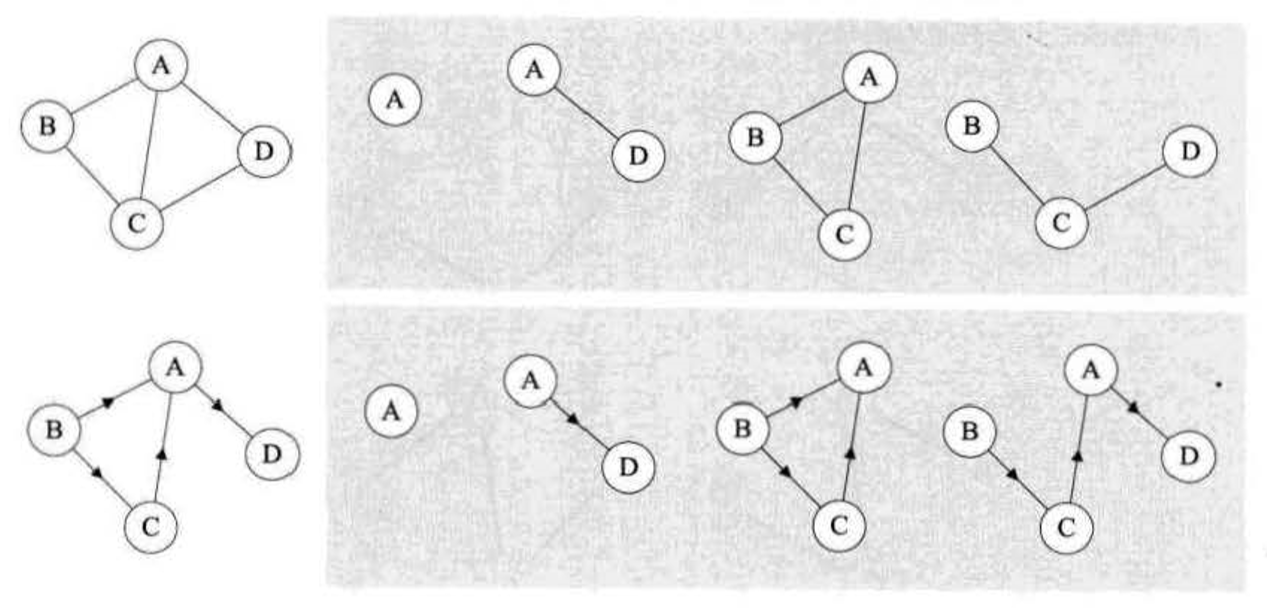
無向圖的度指的是頂點關聯的邊的數量,容易得出總邊數=度的總數/2
有向圖分為出度和入度,以頂點為弧尾的邊的數量為出度,以頂點為弧頂的邊的數量稱為入度。
第一個頂點到最後一個頂點相同的路徑稱為迴路或環 (Cycle)。 序列中頂點不重 復出現的路徑稱為簡單路徑. 除了第一個頂點和最後一個頂點之外,其餘頂點不重複 出現的迴路,稱為簡單迴路或簡單環。
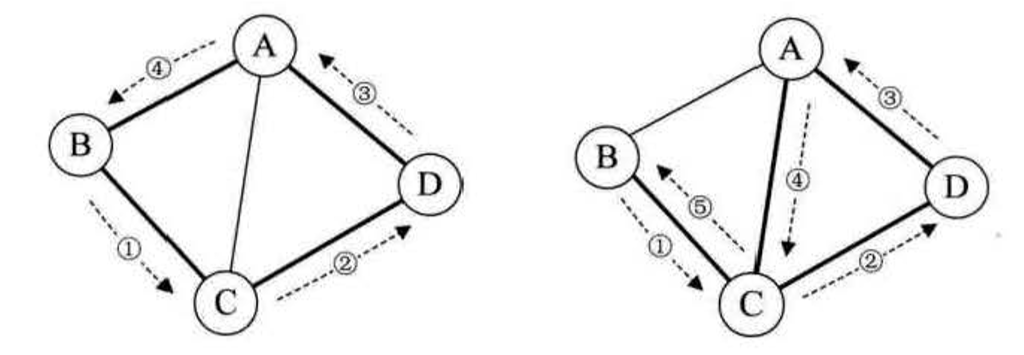
任意頂點都是連通的稱為連通圖。
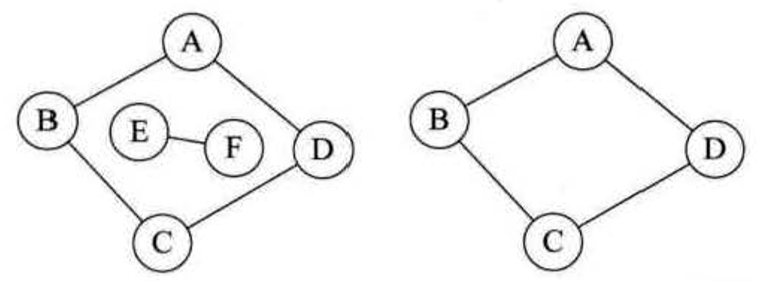
無向圖中的極大連通子圖稱為連通分量。

有向圖中,所有頂點都存在路徑稱為強連通圖,左圖不是強連通圖,右圖是強連通圖,同時右圖是左圖的極大強連通子圖。
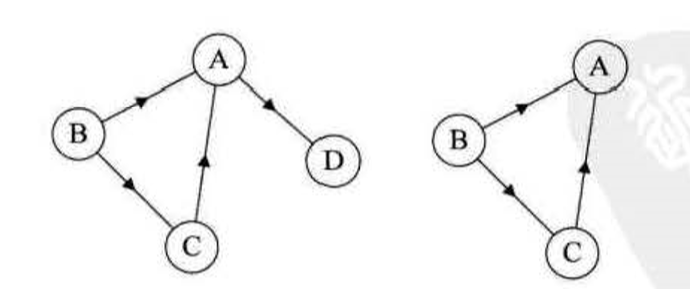
連通圖的生成樹是極小的的連通子圖
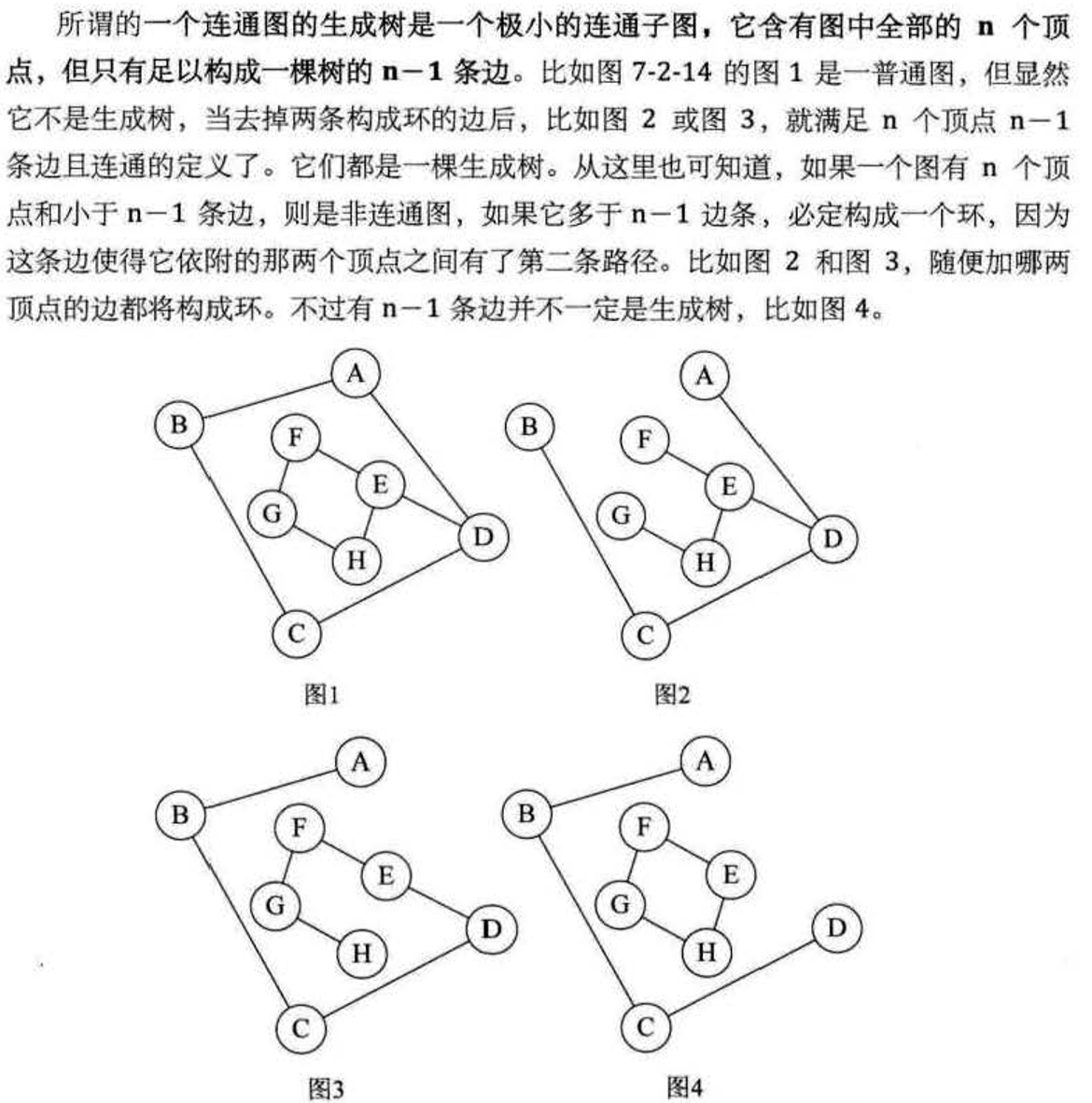
圖通常有五種儲存方式,鄰接矩陣、鄰接表、十字連結串列、鄰接多重表、邊集陣列。
鄰接矩陣用一個一維陣列來表示頂點,用一個二維陣列來表示邊。
對於無向圖來說,矩陣是一個對稱矩陣。
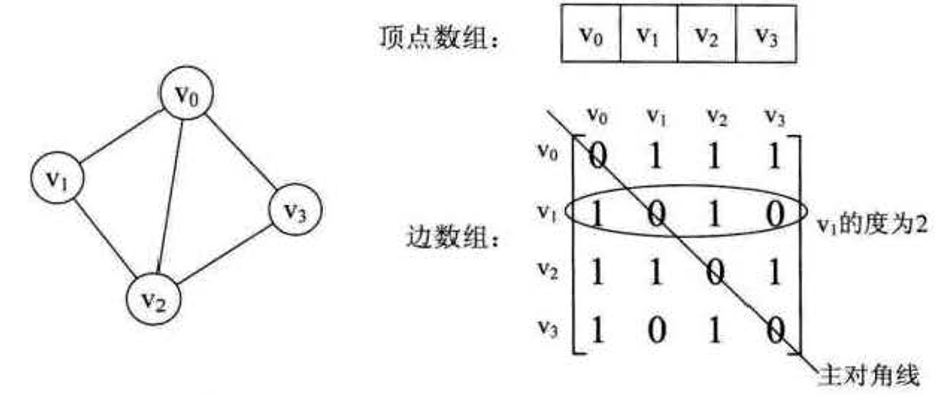
對於有向圖,可以把邊表中沒有弧的地方設為-1。
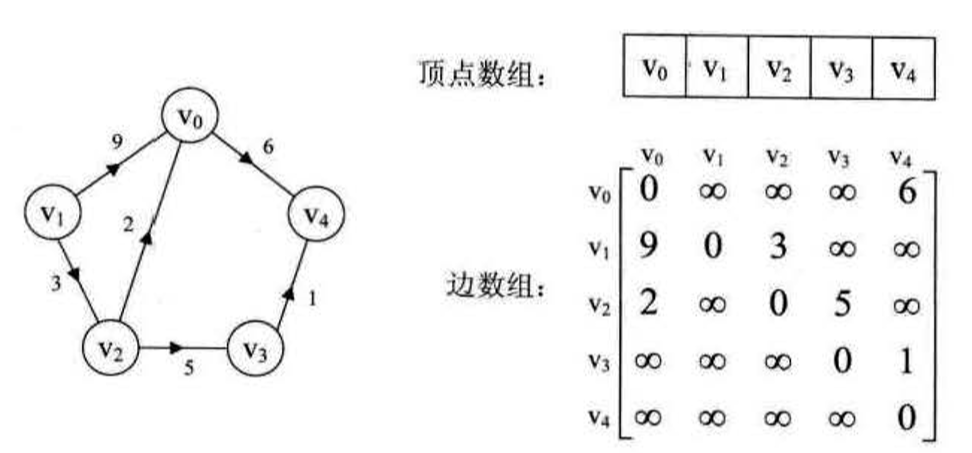
鄰接表是對鄰接矩陣的改進,由於稀疏圖中邊很少,所有二維陣列中很多地方都為0。我們可以用連結串列儲存頂點資訊,同時儲存一個指向邊表的結點。
同一個頂點指向的單鏈表不分先後順序。
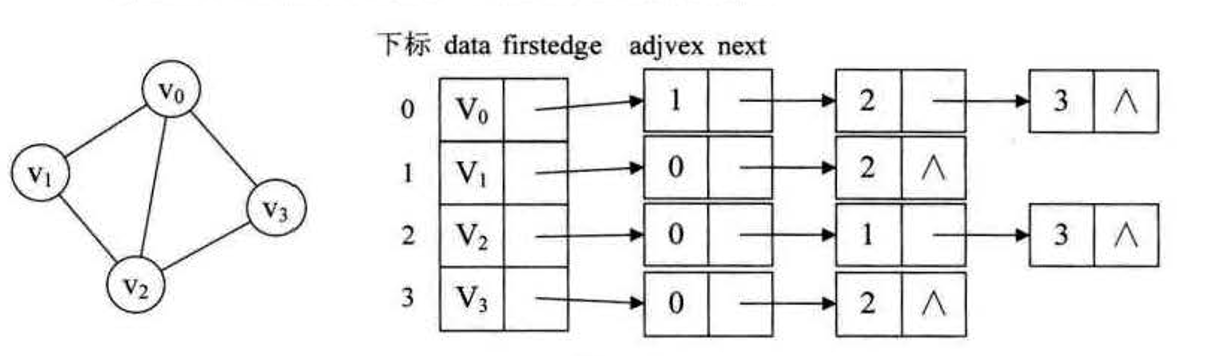
有向圖 的鄰接表(結點不分先後)
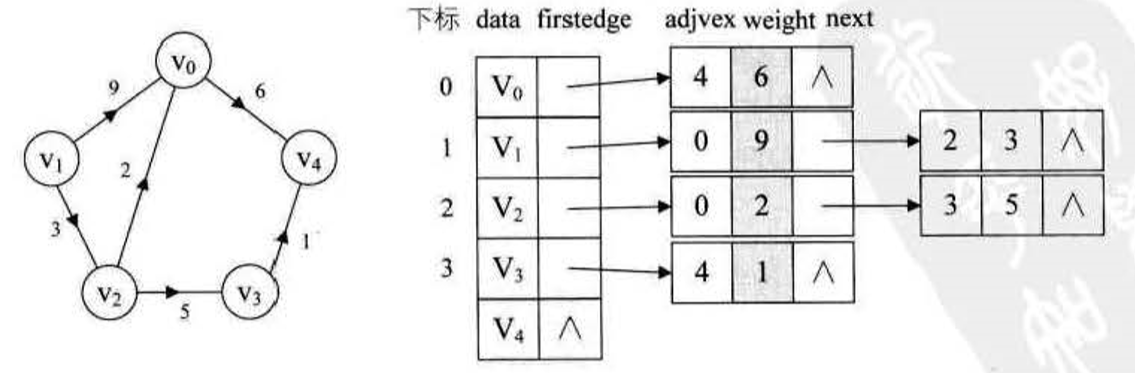
帶權有向圖鄰接表的實現:
package GraphAdjList; import java.util.ArrayList; import java.util.List;//帶權有向圖鄰接表實現(出度表) public class GraphAdjList<T>{ public List<VertexNode<T>> list; public GraphAdjList(T[] datas) { list=new ArrayList<VertexNode<T>>(); System.out.println("初始化頂點表"); for(int i=0;i<datas.length;i++) { VertexNode<T> node=new VertexNode<T>(); node.data=datas[i]; list.add(node); } } //增加頂點 public void insertVertexNode(T x) { VertexNode<T> node=new VertexNode(); node.data=x; System.out.println("新增頂點"); list.add(node); } //遍歷頂點表 public void traversalByVertexNode() { for(VertexNode<T> v:list) { System.out.println(v.data); } } //獲取座標index的頂點 public VertexNode<T> getVertexNode(int index) { return list.get(index); } /** * 新增弧 * @param x 弧頭座標 * @param ajavex 弧尾座標 * @param weight 權值 */ public void addEdge(int x,int ajavex,int weight) { EdgeNode temp=getVertexNode(x).next; while(temp!=null) { temp=temp.next; } EdgeNode node=new EdgeNode(); node.ajavex=ajavex; node.weight=weight; temp.next=node; } } //頂點表 class VertexNode<T> { T data; EdgeNode next;//指向鄰接結點的頭指標 } //邊表 class EdgeNode { int ajavex;//鄰接點座標 int weight;//權值 EdgeNode next;//鄰接點指標 }
測試:
package GraphAdjList; import java.util.List; public class App { public static void main(String[] args) { // TODO Auto-generated method stub String[] str={"V1","V2","V3","V4"}; GraphAdjList<String> g=new GraphAdjList<String>(str); g.traversalByVertexNode(); g.insertVertexNode("V5"); g.traversalByVertexNode(); } }
結果:
初始化頂點表
V1
V2
V3
V4
新增頂點
V1
V2
V3
V4
V5
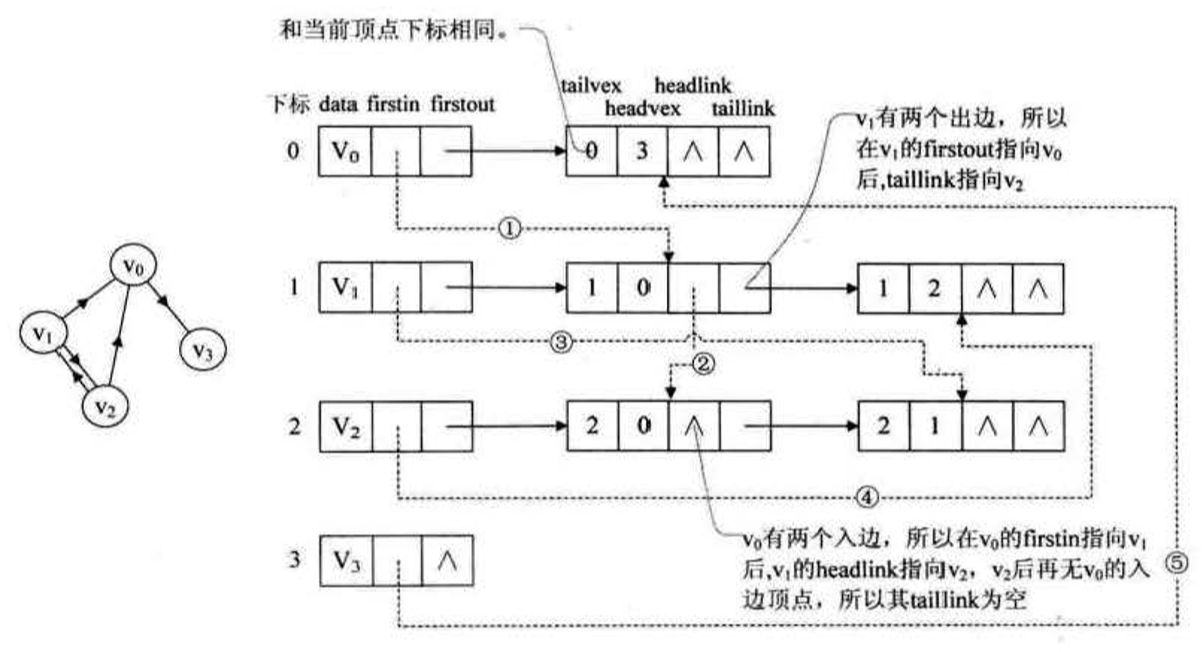
十字連結串列將出度表和入度表結合起來。
頂點表

邊表:

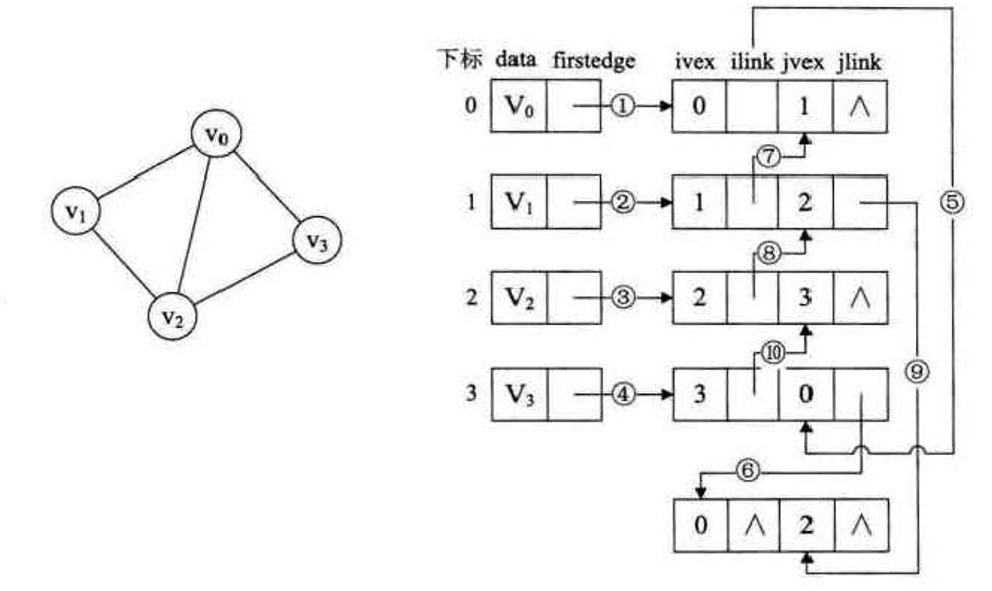
多重鄰接表:無向圖的優化
深度遍歷和廣度遍歷:
深度遍歷類似樹的先序遍歷,始終選取靠左/靠右的頂點,如果某個結點連線的結點都被訪問後則原路返回。用遞迴來實現
廣度遍歷則類似樹的層序遍歷,將每次出隊的頂點的相互連線的頂點入隊,用佇列來來實現

帶權無向圖鄰接矩陣實現,深度遍歷、廣度遍歷:
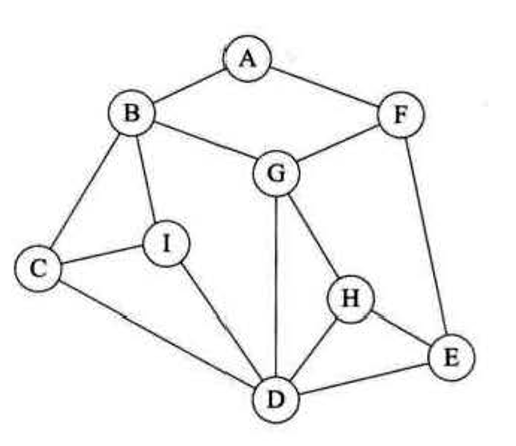
package AMWGraph; import java.util.ArrayList; import java.util.LinkedList; import java.util.List; //帶權無向圖鄰接矩陣實現,深度遍歷、廣度遍歷 public class AMWGraph { public List<Object> vertexList;//結點連結串列 public int[][] edges;//鄰接矩陣 public int numOfEdges;//邊的數目 public boolean[] isVisited; public int count=0; public AMWGraph(int n,String[] v) { isVisited=new boolean[n]; vertexList=new ArrayList<>(); edges=new int[n][n]; for(int i=0;i<n;i++) { vertexList.add(v[i]); isVisited[i]=false; } numOfEdges=0; } //得到結點數目 public int getNumOfVertex() { return vertexList.size(); } //得到邊的數目 public int getNumOfEdges() { return numOfEdges; } //得到結點i的資料 public Object getValueByIndex(int i) { return vertexList.get(i); } //返回v1,v2的權值 public int getWeight(int v1,int v2) { return edges[v1][v2]; } //插入結點 public void insertVertex(Object vertex) { vertexList.add(vertex); System.out.println("增加結點"); int[][] temp=edges; int lengside; lengside=getNumOfVertex(); //頂點數量 edges=new int[lengside][lengside]; for(int i=0;i<temp.length;i++){ for(int j=0;j<temp[i].length;j++) { edges[i][j]=temp[i][j]; } } boolean[] isVisitedTemp=isVisited; isVisited=new boolean[lengside]; for(int i=0;i<isVisitedTemp.length;i++) { isVisited[i]=isVisitedTemp[i]; } isVisited[lengside-1]=false; } //插入邊 public void insertEdge(int v1,int v2,int weight) { edges[v1][v2]=weight; edges[v2][v1]=weight; numOfEdges++; } //刪除邊 public void deleteEdge(int v1,int v2) { edges[v1][v2]=0; numOfEdges--; } //根據一個頂點的下標,返回該頂點的第一個鄰接結點的下標 public int getFirstNeighbor(int index) { for(int j=0;j<vertexList.size();j++) { if(edges[index][j]>0) { return j; } } return -1; } //根據一個鄰接結點的下標來取得下一個鄰接結點的下標 public int getNextNeighbor(int v1,int v2) { for(int j=v2+1;j<vertexList.size();j++) { if(edges[v1][j]>0) { return j; } } return -1; } //深度遍歷 public void depthFirstSearch(boolean[] isVisited,int i) { System.out.println(getValueByIndex(i)); isVisited[i]=true; int w=getFirstNeighbor(i); while(w!=-1) { if(!isVisited[w]) { depthFirstSearch(isVisited,w); } w=getNextNeighbor(i, w); } } //深度優先遍歷 public void depthFirstSearch() { for(int i=0;i<getNumOfVertex();i++) //非連通圖需要選擇多個結點,本結構為連通圖 { if(!isVisited[i]) { count++; depthFirstSearch(isVisited,i); } } } //廣度優先遍歷 private void broadFirstSearch(boolean[] isVisited,int i) { int u,w; LinkedList<Integer>queue=new LinkedList(); System.out.println(getValueByIndex(i)+" "); isVisited[i]=true; queue.addLast(i);//座標進佇列 while(!queue.isEmpty()) { u=((Integer)queue.removeFirst()); w=getFirstNeighbor(i); while(w!=-1) { if(!isVisited[w]) { System.out.println(getValueByIndex(w)+" "); isVisited[w]=true; queue.addLast(w); } w=getNextNeighbor(i, w); } } } //廣度遍歷 public void broadFirstSearch() { for(int i=0;i<getNumOfVertex();i++) { if(!isVisited[i]) { count++; broadFirstSearch(isVisited,i); } } } }
測試:
package AMWGraph; public class App { public static void main(String[] args) { // TODO Auto-generated method stub String[] labels={"A","B","C","D","E","F","G","H","I"}; AMWGraph graph=new AMWGraph(labels.length,labels); graph.insertEdge(0, 1, 1); graph.insertEdge(0, 5, 1); graph.insertEdge(1, 2, 1); graph.insertEdge(1, 8, 1); graph.insertEdge(1, 6, 1); graph.insertEdge(5, 6, 1); graph.insertEdge(2, 3, 1); graph.insertEdge(3, 4, 1); graph.insertEdge(4, 5, 1); graph.insertEdge(6, 7, 1); graph.insertEdge(3, 7, 1); graph.insertEdge(3, 6, 1); System.out.println("結點個數:"+graph.getNumOfVertex()); System.out.println("邊個數:"+graph.getNumOfEdges()); // graph.depthFirstSearch(); // System.out.println(graph.count); graph.broadFirstSearch(); System.out.println(graph.count); } }
結果:
DFS 結點個數:9 邊個數:12 A B C D E F G H I 重新選擇結點次數:1 BFS 結點個數:9 邊個數:12 A B F C D E G H I 重新選擇結點次數:5
