二叉樹的問題(更新ing)
前言
在有序陣列中,可以快速找到特定的值,但是想在有序陣列中插入一個新的資料項,就必須首先找出新資料項插入的位置,然後將比新資料項大的資料項向後移動一位,來給新的資料項騰出空間,刪除同理,這樣移動很費時。顯而易見,如果要做很多的插入和刪除操作和刪除操作,就不該選用有序陣列。
另一方面,連結串列中可以快速新增和刪除某個資料項,但是在連結串列中查詢資料項可不容易,必須從頭開始訪問連結串列的每一個數據項,直到找到該資料項為止,這個過程很慢。
關於樹
樹這種資料結構,既能像連結串列那樣快速的插入和刪除,又能想有序陣列那樣快速查詢。這裡主要實現一種特殊的樹——二叉(搜尋)樹。二叉搜尋樹有如下特點:一個節點的左子節點的關鍵字值小於這個節點,右子節點的關鍵字值大於或等於這個節點。插入一個節點需要根據這個規則進行插入。
刪除節點時二叉搜尋樹中最複雜的操作,但是刪除節點在很多樹的應用中又非常重要,所以詳細研究並總結下特點。刪除節點要從查詢要刪的節點開始入手,首先找到節點,這個要刪除的節點可能有三種情況需要考慮。
-
該節點是葉節點,沒有子節點
-
該節點有一個子節點
-
該節點有兩個子節點
- 第一種最簡單,第二種也還是比較簡單的,第三種就相當複雜了。下面分析這三種刪除情況:
要刪除葉節點,只需要改變該節點的父節點對應子欄位的值即可,由指向該節點改為 null 就可以了。垃圾回收器會自動回收葉節點,不需要自己手動刪掉;當節點有一個子節點時,這個節點只有兩個連線:連向父節點和連向它唯一的子節點。需要從這個序列中剪斷這個節點,把它的子節點直接連到它的父節點上即可,這個過程要求改變父節點適當的引用(左子節點還是右子節點),指向要刪除節點的子節點即可;第三種情況最複雜,如果要刪除有兩個子節點的節點,就不能只用它的一個子節點代替它,比如要刪除節點25,如果用35取代它,那35的左子節點是15呢還是30?
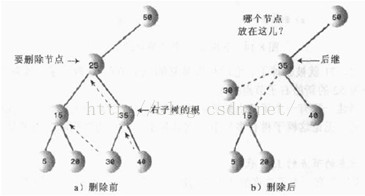
因此需要考慮另一種方法,尋找它的中序後繼來代替該節點。下圖顯示的就是要刪除節點用它的後繼代替它的情況,刪除後還是有序的。(這裡還有更麻煩的情況,即它的後繼自己也有右子節點,下面再討論。)

那麼如何找後繼節點呢?首先得找到要刪除的節點的右子節點,它的關鍵字值一定比待刪除節點的大。然後轉到待刪除節點右子節點的左子節點那裡(如果有的話),然後到這個左子節點的左子節點,以此類推,順著左子節點的路徑一直向下找,這個路徑上的最後一個左子節點就是待刪除節點的後繼。如果待刪除節點的右子節點沒有左子節點,那麼這個右子節點本身就是後繼。尋找後繼的示意圖如下:

找到了後繼節點,現在開始刪除了,先看第一種情況,後繼節點是delNode右子節點的做後代,這種情況要執行以下四個步驟:
-
把後繼父節點的leftChild欄位置為後繼的右子節點;
-
把後繼的rightChild欄位置為要刪除節點的右子節點;
-
把待刪除節點從它父節點的leftChild或rightChild欄位刪除,把這個欄位置為後繼;
-
把待刪除的左子節點移除,將後繼的leftChild欄位置為待刪除節點的左子節點。
這下圖所示:

如果後繼節點就是待刪除節點的右子節點,這種情況就簡單了,因為只需要把後繼為跟的子樹移到刪除的節點的位置即可。如下圖所示:

看到這裡,就會發現刪除時相當棘手的操作。實際上,因為它非常複雜,一些程式設計師都嘗試著躲開它,他們在Node類中加了一個Boolean欄位來標識該節點是否已經被刪除,在其他操作之前會先判斷這個節點是不是已經刪除了,這樣刪除節點不會改變樹的結構。當然樹中還保留著這種已經刪除的節點,對儲存造成浪費,但是如果沒有那麼多刪除的話,這也不失為一個好方法。
- 另外二叉樹有三種遍歷方式:前序、中序和後序。這個比較簡單,直接看下程式碼即可。
Public class BinaryTree {
private BNode root;//根節點
public BinaryTree() {
root = null;
}//二叉搜尋樹查詢的時間複雜度為O(logN) public BNode find(int key) {//find node with given key BNode current = root;
while(current.key != key) {
if(key < current.key) {
current = current.leftChild;
}
else {
current = current.rightChild;
}
if(current == null) {
return null;
}
}
return current;
}//插入節點 public void insert(int key, double value) {
BNode newNode = newBNode();
newNode.key = key;
newNode.data = value;
if(root == null) {//if tree is null
root = newNode;
}
else {
BNode current = root;
BNode parent;
while(true) {
parent = current;
if(key < current.data) {//turn left
current = current.leftChild;
if(current == null) {
parent.leftChild = newNode;
newNode.parent = parent;
return;
}
}
else {//turn right
current = current.rightChild;
if(current == null) {
parent.rightChild = newNode;
newNode.parent = parent;
return;
}
}
}
}
}//遍歷二叉樹
public void traverse(int traverseType) {
switch(traverseType) {
case 1: System.out.println("Preorder traversal:");
preOrder(root);//前向遍歷
break;
case 2: System.out.println("Inorder traversal:");
inOrder(root);//中向遍歷
break;
case 3: System.out.println("Postorder traversal:");
postOrder(root);//後向遍歷
break;
default: System.out.println("Inorder traversal:");
inOrder(root);
break;
}
System.out.println("");
}//前向遍歷
private void preOrder(BNode localRoot) {
if(localRoot != null) {
System.out.print(localRoot.data + " ");
preOrder(localRoot.leftChild);
preOrder(localRoot.rightChild);
}
}//中向遍歷
private void inOrder(BNode localRoot) {
if(localRoot != null) {
inOrder(localRoot.leftChild);
System.out.print(localRoot.data + " ");
inOrder(localRoot.rightChild);
}
}//後向遍歷
private void postOrder(BNode localRoot) {
if(localRoot != null) {
postOrder(localRoot.leftChild);
postOrder(localRoot.rightChild);
System.out.print(localRoot.data + " ");
}
}//查詢最小值 /*根據二叉搜尋樹的儲存規則,最小值應該是左邊那個沒有子節點的那個節點*/
public BNode minNumber() {
BNode current = root;
BNode parent = root;
while(current != null) {
parent = current;
current = current.leftChild;
}
return parent;
}//查詢最大值 /*根據二叉搜尋樹的儲存規則,最大值應該是右邊那個沒有子節點的那個節點*/
public BNode maxNumber() {
BNode current = root;
BNode parent = root;
while(current != null) {
parent = current;
current = current.rightChild;
}
return parent;
}//刪除節點 /* * 刪除節點在二叉樹中是最複雜的,主要有三種情況: * 1. 該節點沒有子節點(簡單) * 2. 該節點有一個子節點(還行) * 3. 該節點有兩個子節點(複雜) * 刪除節點的時間複雜度為O(logN) */
public booleandelete(int key) {
BNode current = root;// BNode parent = root;
boolean isLeftChild = true;
if(current == null) {
return false;
}//尋找要刪除的節點
while(current.data != key) {// parent = current;
if(key < current.key) {
isLeftChild = true;
current = current.leftChild;
}
else {
isLeftChild = false;
current = current.rightChild;
}
if(current == null) {
return false;
}
}//找到了要刪除的節點,下面開始刪除 //1. 要刪除的節點沒有子節點,直接將其父節點的左子節點或者右子節點賦為null即可
if(current.leftChild == null && current.rightChild == null) {
return deleteNoChild(current, isLeftChild);
}//3. 要刪除的節點有兩個子節點
elseif(current.leftChild != null && current.rightChild != null) {
return deleteTwoChild(current, isLeftChild);
}//2. 要刪除的節點有一個子節點,直接將其砍斷,將其子節點與其父節點連起來即可,要考慮特殊情況就是刪除根節點,因為根節點沒有父節點
else {
return deleteOneChild(current, isLeftChild);
}
}
public boolean deleteNoChild(BNode node, boolean isLeftChild) {
if(node == root) {
root = null;
return true;
}
if(isLeftChild) {
node.parent.leftChild = null;
}
else {
node.parent.rightChild = null;
}
return true;
}
public boolean deleteOneChild(BNode node, boolean isLeftChild) {
if(node.leftChild == null) {
if(node == root) {
root = node.rightChild;
node.parent = null;
return true;
}
if(isLeftChild) {
node.parent.leftChild = node.rightChild;
}
else {
node.parent.rightChild = node.rightChild;
}
node.rightChild.parent = node.parent;
}
else {
if(node == root) {
root = node.leftChild;
node.parent = null;
return true;
}
if(isLeftChild) {
node.parent.leftChild = node.leftChild;
}
else {
node.parent.rightChild = node.leftChild;
}
node.leftChild.parent = node.parent;
}
return true;
}
public boolean deleteTwoChild(BNode node, boolean isLeftChild) {
BNode successor = getSuccessor(node);
if(node == root) {
successor.leftChild = root.leftChild;
successor.rightChild = root.rightChild;
successor.parent = null;
root = successor;
}
elseif(isLeftChild) {
node.parent.leftChild = successor;
}
else {
node.parent.rightChild = successor;
}
successor.leftChild = node.leftChild;//connect successor to node's left child
return true;
}//獲得要刪除節點的後繼節點(中序遍歷的下一個節點)
public BNode getSuccessor(BNode delNode) {
BNode successor = delNode;
BNode current = delNode.rightChild;
while(current != null) {
successor = current;
current = current.leftChild;
}
if(successor != delNode.rightChild) {
successor.parent.leftChild = successor.rightChild;
if(successor.rightChild != null) {
successor.rightChild.parent = successor.parent;//刪除後續節點在原來的位置}
successor.rightChild = delNode.rightChild;//將後續節點放到正確位置,與右邊連上
}
return successor;
}
}
classBNode {
public int key;
public double data;
public BNode parent;
public BNode leftChild;
public BNode rightChild;
public void displayNode() {
System.out.println("{
" + key + ":" + data + "}
");
}
}
參考資料:(程式碼整理有點亂,多多包涵哈!)
