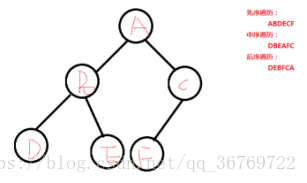
《資料結構》筆記
字首表示式:也成為波蘭表示式 *23+1-4
中綴表示式:最常用的那種 1+2*3-4
字尾表示式:為了區分字首,也稱為逆波蘭表示式 123*+4-
使用三個結點三個結點檢視的方式更明顯
圖:
圖中的專業術語:
圖定義:
圖是由頂點的有窮非空集合和頂點之間邊的集合組成,通常表示為:G(V,E)
其中,G表示是一個圖,V是圖G中頂點的集合,E是圖G中的邊的集合
頂點:
線性表中將資料元素叫做元素,樹中將資料元素叫做結點,在圖中資料元素稱之為頂點(Vertex)
線性表樹和圖之間的不同:
1、線性表中可以沒有資料元素稱為空表,樹中可以沒有結點稱做空樹,但是在圖中不允許沒有頂點
2、線性表中相鄰的元素之間具有線性關係,樹結構中相鄰兩層的節點具有層次關係,但是在圖中
任意兩個頂點之間都可能有關係,頂點之間的邏輯關係用邊來表示,邊集可以是空的
各種圖定義:
無向邊:
若頂點vi到vj之間的邊沒有方向,則這條邊稱為無向邊(Edge),用無序偶對(vi,vj)來表示。
如果圖中任意兩條邊都是無向的,那麼該圖稱做無向圖
有向邊:
若從頂點vi到vj的邊有方向,則稱這條邊為有向邊,也稱為弧(Arc)
資料結構:
樹狀結構的幾種表示方法:
第一種:畫倒立樹表示
第二種:巢狀集合表示法(圓圈包含)
第三種:凹入表表示法(使用長條長短來進行表示)
第四種:廣義表表示法(使用括號包含來表示)
樹形結構術語:
在一課非空樹中,有且只有一個根結點
節點的度:有幾個孩子就成為該結點的度為多少
樹的度: 是節點的度最大的那一個就是樹的度
葉子節點(終端節點):度為零的節點成為葉子節點
非終端節點:度不為零的節點
除根節點之外的節點統稱為內部節點
雙親節點:
節點層數:
樹的高度:最底下一層節點的層數
有序樹:樹中的每一個節點是有次序的,從左至右,不能交換
無序樹:樹中每一個節點是沒有次序的,是可以交換的
森林:
對於模板類中還有一個類的話,如果函式返回值是類中類的型別,那麼儘量寫在類內部來實現該函式,寫在外面會有點複雜,很容易就出錯了(雖然編譯能夠通過,但是一使用就會報錯的)
連結串列使用結點
樹使用節點(一個節點就是一棵樹)
設計一個n叉樹的結構:
因為不知道一個節點有幾個孩子,所以可以使用一個指標陣列,將每一個指標都指向一個節點的孩子,還有一個父節點指標,以及一個數據域,但是這樣設計的結構如果需要不斷插入到一個節點的孩子或者兄弟節點的話,就需要重複申請指標陣列,將原來的指標執行拷貝到新的指標陣列中,這樣會浪費開銷
現在設計的一個結構是由一個數據域,一個指向父節點的指標域,還有一個指向兄弟節點的指標這樣不管你有多少個孩子直接在最後一個兄弟之後進行插入就可以了
對於這樣的結構插入情況:
在哪個節點之後進行插入,插入到是什麼地方
如果沒有找到要插入的節點,那麼需要設計一個規則,將要插入的資料作為最後一層的第一個節點的孩子,如果找到了,如果找到了那麼看是插入到哪個地方,如果是作為找到的節點的孩子的話,那麼放在孩子節點的最後一個兄弟的後面,如果是兄弟,那麼放在最後一個兄弟的兄弟,這樣插入搞定
有序樹:
所謂有序樹就是按照指定的某個規則進行構建的一個樹,然後按照先序中序後序其中的一個方式進行遍歷就是有序的,這樣的樹就是一個有序樹,如果不論用哪種方式進行遍歷都是沒有順序的,那麼這樣的樹就是一個無序樹
另外需要注意的是:有序樹不一定是一個完全二叉樹,如果是將根作為最大或者最小的資料,那麼這樣構建出來的樹就是一個堆了,所謂堆就是一個完全二叉樹,有自己的插入刪除規則,執行完任何操作之後要仍然保證是一個大頂堆或小頂堆
有序二叉樹的使用遞迴方式插入(定義規則:左子樹資料 < 根資料 <= 右字樹資料)
void _insert(TreeNode **root,T const &date) //往有序樹中使用遞迴插入節點
{ //必須使用二級指標才行,因為需要在函式中改變root的資料
if(*root)
{
if((*root)->date>date)
{
_insert((*root)->left,date);
}
else
{
_insert((*root)->right,date);
}
}
else
{
*root=_createNode(date);
}
}有序二叉樹的刪除:
根據節點中的資料,刪除有序二叉樹中的節點
1、能找到
1.1是根節點
1.1.1有右字樹
將右字樹的最小資料的節點的左孩子指標指向根結點的左孩子
1.1.2沒有右字樹
將pRoot指標直接指向pRoot的左孩子指標
1.2是子樹
滿二叉樹:
滿二叉樹中第i層上的節點個數為2的i-1次方個
深度為n的二叉樹中所有的節點個數之和為2的i次方-1個
對於任意的一個二叉樹中滿足葉子節點個數=度為2的節點個數+1
滿二叉樹:
完全二叉樹:如果一棵二叉樹最多隻有最下面的兩層其節點的度數可以小於2,並且最下一層的節點全部集中在左邊
滿二叉樹是一棵特殊的完全二叉樹,反之不是
使用順序結構來實現完全二叉樹是比較方便的,而且也節約空間:
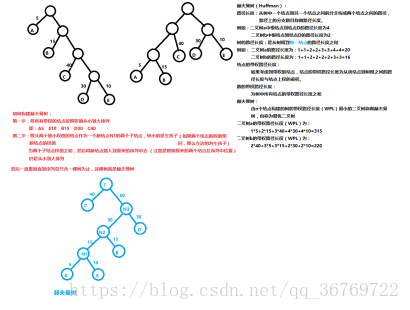
哈夫曼樹:
最優二叉樹,所有節點的帶權路徑之和最小
用法:使用頻率越高的資料越放在前面,頻率越低的資料放下面
更多的作用用在搜尋資料
構建哈夫曼樹的規則是首先找到所有元素中的權值最小的兩個節點,然後將這兩個節點構建成一個樹,然後在剩下的元素中取權值最小的元素和構建成的樹的父節點組成一個新的樹,重複這個操作將所有的元素都插入到整個二叉樹當中,這樣構建出來的就是一個哈夫曼樹也就是最優二叉樹了
堆:完全二叉樹的一種表現形式
最大(小)完全二叉樹也叫大頂堆小頂堆
在這個樹中每一個父節點的值是大(小)於或者等於孩子節點的值就成為大頂堆
1、堆的插入
首先將要插入的資料放在陣列的最後,然後和當前節點的父節點進行比較,看是否滿足 原來的堆規則,如果不滿足,那麼和父節點進行交換位置,一直交換到滿足了原來的堆 的結構為止
2、堆的刪除
直接將最後一個元素覆蓋將被刪除的元素位置,然後往下找此時被刪除位置元素的正確位置,這樣就完成了堆元素的刪除
總之目的只有一個在進行元素的插入和刪除操作之後保證改變後的堆仍然是一個和原來堆一樣的結構就可以了
3、堆的初始化
深度尋路(DFS):
深度尋路所謂深度就是指的按照一條路徑走到底,如果可以到達目的地,那麼這就算找到了一條路徑,不會管是不是還有其他更短的路徑可走的
深度尋路在空曠的地圖上進行尋路比較合適
那麼廣度尋路是找到的路徑最短的一條路線,廣度比深度複雜,迴圈成本高,遍歷地圖越大越慢,一般在小地圖裡面,找任意最短用廣度
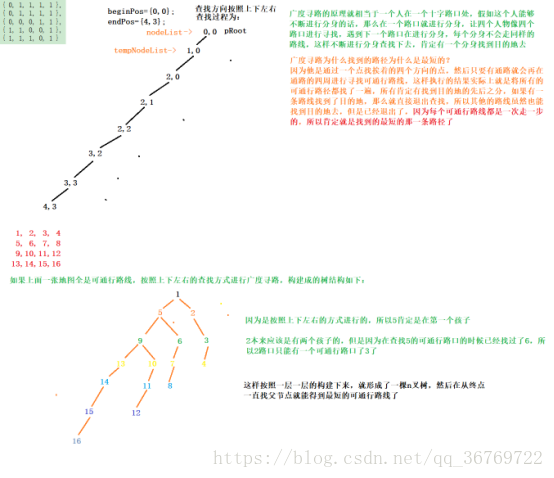
廣度尋路(BFS):廣度優先演算法
廣度尋路是一個樹狀結構
深度是一個上一節點找下一個節點
廣度是上一個節點找下幾個節點
深度游回退,廣度沒有回退
因為廣度尋路需要進行構建一棵樹結構,所以如果要進行尋路的地圖很空曠,那麼構建出來的樹就會很大,所以廣度尋路是不太適合地圖較大,地圖比較空曠的情況的。這樣情況用深度尋路會比較好
補充:
二叉排序樹(Binary Sort Tree),又稱為二叉查詢樹。它或者是一棵空樹,或者是具有下列性質的二叉樹:
1、若它的左子樹不空,則左子樹上所有節點的值均小於它的根結點的值
2、若它的右字樹不空,則右字樹上所有節點的值均大於它的根結點的值
3、它的左右子樹也分別為二叉排序樹
實際上二叉排序樹就是有序二叉樹
堆結構:
堆是具有下列性質的完全二叉樹:每個節點的值都大於或等於其左右孩子節點的值,稱為大頂堆;或者每個節點的值都小於或等於其左右孩子節點的值,稱為小頂堆
堆排序:(Heap Sort)
堆排序就是利用堆(假設利用大頂堆)進行排序的方法。它的基本思想是,將待排序的序列構造成一個大頂堆。此時,整個序列的最大值就是堆頂的根結點。將他移走(其實就是將其和堆陣列的末尾元素交換,此時末尾元素就是最大值),然後將剩餘的n-1個序列重新構造成一個堆,這樣就會得到n個元素中的次小值,如此反覆執行,便能得到一個有序序列了
A*尋路:
優點:尋路能夠找到最短路徑,開銷比廣度尋路要小,尋路中會將一些路徑丟棄掉
缺點:程式碼的會比較複雜點,需要考慮的東西有點多
深度在空曠的環境中,並且最好也知道目的地相對起點的大概位置是比較適合的
廣度適合在小範圍尋路是比較適合的,可以找到所有路徑
A*在大範圍的地圖中一定要使用A*
A*只能找到一條最短路徑
A*尋路使用最多的一種尋路演算法
A*尋路是啟發式搜尋,在地圖空間中對每一個待搜尋位置進行評估,得到最優位置,從最優位置進行尋路
啟發式的搜尋評估的公式:
f=g+h;
F:節點評估值f值越小,路勁越優,優先搜尋
G:從初始點到當前點需要多少代價(花費多長的時間或者多上的精力)
H:從當前點到終點的預估代價,預估代價走直線,且忽視障礙
A星尋路和深度廣度尋路最大的區別:A星尋路可以走斜路,廣度深度只能走直線
A*尋路過程例項分析:
例如上圖:如果小貓想要從當前位置去遲到牆壁右邊的骨頭的按照A*尋路過程分析:
首先小貓一開始的位置對四周四個位置(如果有障礙物則不考慮)進行判斷f的值,可以得到小貓右邊位置的f值是最小的,那麼就將小貓一開始的位置放入close列表中,將右邊的位置放入open列表中,然後將右邊的位置作為開始位置,對該位置進行檢視四周f值的判斷操作,然後可以得到下面的位置f值是最小的,重複操作,將這次的當前位置從open列表中移入close列表中,將這次找到的f值最小的位置放到open列表中,然後對這次的open中的位置進行四周檢視f值操作,得到下面的位置f值是最小的
紅黑樹:
紅黑樹是一種特殊的二叉查詢樹,它能保證在最壞情況下基本操作的時間複雜度為O(log2N)。這種資料結構避免了普通二叉樹基本操作與樹高度成正比的劣勢,是一種常用的重要資料結構。
一棵滿足紅黑性質的二叉查詢樹就是紅黑樹(前提條件是二叉查詢樹,即滿足左<根<右)
紅黑樹必須滿足的性質:
1、每個節點或者是紅的,或者是黑的
2、根節點一定是黑
3、葉節點一定是黑的
4、如果一個節點是紅的,那麼它的兩個孩子節點都是黑的(反之說也就是黑的父必是紅)
5、對每個節點,對該節點到其子孫節點的所有路徑上包含相同數目的黑節點
平衡二叉樹
平衡二叉樹是一種二叉排序樹,其中每一個節點的左子樹和右字樹的高度差至多等於1
平衡二叉樹是一種高度平衡的二叉排序樹
我們將二叉樹上節點的左子樹深度減去右字樹深度的值稱為平衡因子BF(Balance Factor),那麼平衡二叉樹上所有節點的平衡因子只可能是-1,0,1,只要二叉樹上有一個節點的平衡因子的絕對值大於1,那麼該二叉樹就是不平衡的
最小不平衡樹:
距離插入節點最近的,且平衡因子的絕對值大於1的節點的為根的子樹,我們稱為最小不平衡子樹
平衡二叉樹實現原理:
平衡二叉樹構建的基本思想就是在構建二叉排序樹的過程中,每當插入一個節點時,先檢查是否因插入而破壞了樹的平衡性,若是,則找出最小不平衡樹。在保持二叉排序樹特性的前提下,調整最小不平衡子樹中個結點之間的連結關係,進行相應的旋轉,使之成為新的平衡二叉樹
雜湊表
Hash:雜湊,也叫做散列表,是一種無序儲存,所謂無序就是自己構建地址,不一定是記憶體地址
自己構建地址:地址和值的關係,這種關係稱之為雜湊函式
學習雜湊表,最重要的就是雜湊函式的構造,所謂雜湊函式就是地址和值的對映
製作雜湊函式幾種常用的方法:
第一種:
餘數法 H(key)=key%p; //p是個常量,自己設定
例如將p設定為10的話:
那麼有:
H(key)=key%10;
3 12 46 37 48
Arr[3%10]=3;
Arr[12%10]=12;
Arr[46%10]=46;
Arr[37%10]=37;
Arr[48%10]=48;
會發現陣列下標有重複的,這種情況就稱為雜湊衝突
第二種:平方取中法:
1234^2=1522756 h(key)=227;
第三種:直接定址法
H(key)=key;
3 12 46 37 48
Arr[3]=3;
Arr[12]=12;
Arr[46]=46;
Arr[37]=37;
Arr[48]=48;
第四種:摺疊法(比較適合大數)
雜湊表:
雜湊法又名雜湊法,是一種特殊的查詢方法,查詢很循序
理想查詢方法是不經過比較
如果有一種方法不經過比較,就能找到,這樣就是最理想的查詢
雜湊法就是這種查詢方式,不經過比較
雜湊表中衝突現象
設計一個雜湊表需要做的準備工作:
1、確定表的範圍
2、構造合適的雜湊函式
雜湊表的構建就是通過陣列和連結串列進行組合的方式構建的一種結構
陣列是一個指標陣列,每一個下標資料都代表一種資料型別,然後用該下標的指標最為該型別的連結串列頭,這一類的資料都放在這個連結串列中
雜湊表的其實就是通過將資料進行分類,然後將每一類資料都用連結串列來存放,這樣查詢的時候根據關鍵字,也就是下標了,然後直接在該關鍵字型別代表的連結串列中進行查詢資料,這樣對於大量的資料進行查詢就非常方便快速了
解決雜湊衝突的兩種方法:
第一種:開放地址法
線型探測的方法
第二種:陣列連結串列法
做的事情:
1、實現雜湊
2、解決雜湊表的衝突
3、雜湊表的查詢
4、雜湊表的列印
有什麼用處:對資料進行加密操作
歸併排序:
兩個有序數組合併成一個有序陣列就叫歸併排序