梯度下降法/批量梯度下降法BGD

梯度下降法是一種基於搜尋的最優化方法,即通過不斷地搜尋找到函式的最小值.並不是機器學習專屬的方法.但是在機器學習演算法中求解損失函式的最小值時很常用.

還記得之前說過的機器學習演算法的普遍套路嗎？

1. 定義一個合理的損失函式
2. 優化這個損失函式,求解最小值.

對有的損失函式來說,最小值是有著數學上的方程解的.但有的函式是不存在著數學解的,這時候我們就可以通過梯度下降法逐步地搜尋,直到越來越逼近最優解.

首先我們要理解梯度的概念:

梯度的本意是一個向量（向量），表示某一函式在該點處的方向導數沿著該方向取得最大值，即函式在該點處沿著該方向（此梯度的方向）變化最快，變化率最大（為該梯度的模）。

這裡有篇很棒的講解,幫助你理解梯度,主要是圖很多,很直觀.建議看看.

1. 基本概念 .這幾個基本概念一定要搞清楚.    

• 方向導數：是一個數；反映的是f(x,y,z...)沿方向v的變化率。      
• 偏導數：是多個數（每元有一個).是指多元函式沿座標軸方向的方向導數，因此二元函式就有兩個偏導數。      
• 偏導函式：是一個函式；是一個關於點的偏導數的函式。      
• 梯度：是一個向量；每個元素為函式對一元變數的偏導數；它既有大小（其大小為最大方向導數），也有方向。

函式沿著梯度的方向增大最快。注意不要用一元函式的思維去思考這個結論.梯度是有方向的！不要把梯度和導數搞混了,比如$y=x^2$的導數y=2x，如果非要把導數表述成說梯度的話,梯度的方向其實是x軸.在x<0時,x處的導數為負,那麼梯度為x軸反方向的向量,x>0時,梯度為x軸方向的向量,此時,函式沿著梯度的方向增大最快這個結論依然是成立的.

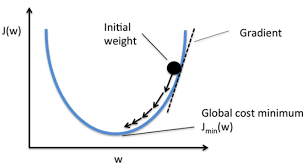
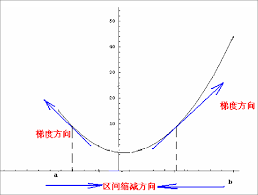
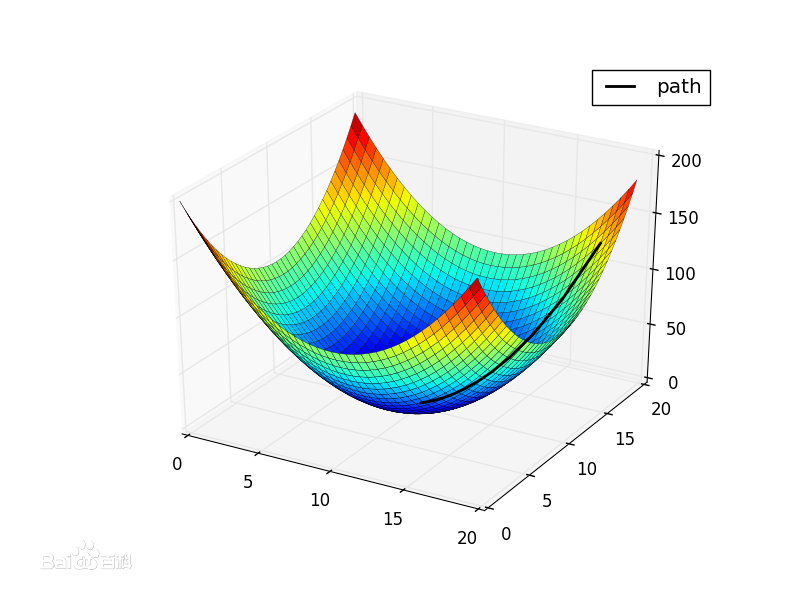
我們現在要求$J(\theta)$的最小值.則從某個點A開始,每次沿著A點的梯度的反方向移動$\eta$到點B,到達B點後,再沿著B點的梯度的反方向移動$\eta$,....,不斷重複這個過程,最終就可以達到某一個極值點.

直觀點說,比如我們在一座大山上的某處位置A，我們想下山,想最快地下山,於是我們求出A點梯度$\nabla_A$（這是一個向量,沿著這個方向的反方向即下山的最陡峭的路），然後移動$- \eta\nabla_A$到達位置B，求出$\nabla_B$，移動$- \eta\nabla_B$到達位置C，......不斷重複這一過程,最終就達到了山底.也有可能只是區域性的山底.

$\eta$稱作學習率

1. $\eta$影響獲得最優解的速度
2. $\eta$選取的不好 甚至無法找到最優解

對第一點很好理解,$\eta$太小了,勢必要很久才能達到極值點.

對第二點,試想,如果$\eta$太大,則有可能錯過極值點.比

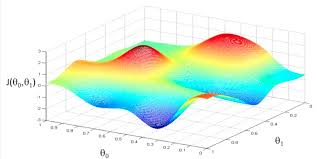
不是所有函式都只有唯一極值點的.所以梯度下降法找到的可能是區域性最小值而不是全域性最小值.結合下圖理解一下.所以我們的起始搜尋點就很重要了.

結合上面說的下山的例子理解一下,即

1. 起始位置A很重要   實際使用中通常要多次隨機生成這個A的位置,以避免找到的是區域性最優解而不是全域性最優解
2. 學習率$\eta$很重要.需要我們不斷除錯.屬於一個超引數.
3. 通常在使用梯度下降法之前,需要對資料做歸一化處理,避免某一維度資料尺度過大,影響梯度的值.影響收斂速度.

實現線性迴歸中的梯度下降法

機器學習筆記線性迴歸中我們推匯出$f_{loss} = \sum_{i=1}^m(y^i - X_b^i  \theta)^2$.之後如何求得$\theta$,可以使得對所有樣本而言,損失最小.我們一筆帶過了.這個函式是有著其數學解的.但是今天我們用梯度下降法求出$\theta$。

$$\nabla L(\theta) = \begin{bmatrix}  \frac {\partial L} {\partial \theta_0} \\  \frac {\partial L} {\partial \theta_1} \\  \frac {\partial L} {\partial \theta_2} \\  … \\  \frac {\partial L}{\partial \theta_n} \\  \end{bmatrix} = \begin{bmatrix}  \sum_{i=1}^m 2(y^{(i)}-X_b^{(i)}\theta)(-1) \\  \sum_{i=1}^m 2(y^{(i)}-X_b^{(i)}\theta)(-X_1^{(i)}) \\  \sum_{i=1}^m 2(y^{(i)}-X_b^{(i)}\theta)(-X_2^{(i)}) \\  … \\  \sum_{i=1}^m 2(y^{(i)}-X_b^{(i)}\theta)(-X_n^{(i)}) \\  \end{bmatrix}$$

偽碼如下：

注意:未知數是theta，而不是X_b,y。 

#某一種theta取值下  獲取其對應的梯度向量
def  get_gradient(X_b,y,theta):
　　 return gradient  #這裡返回的是一個向量

#損失函式的大小
#def loss(X_b,y,theta):
　　return loss_value  #當theta取某種值時,loss的大小   是一個數

def gradient_descent(init,eta,n,diff=1e-8):  #init代表起始點位置  eta代表步長 n代表最大迭代次數
    theta =  init
    
    i = 0
    while i < n:
　　   gradient = get_gradient(X_b,y,theta):
      new_theta = theta - eta*get_gradient()  #移動到新位置
      
      #當兩點直接損失函式值相差極小,說明我們已經逼近區域性最小值
      if abs(loss(X_b,y,theta) - loss(X_b,y,new_theta)) < diff：   #類似與c++中判斷浮點數是否為0.
            break
            
      theta = new_theta

這是代數方法,還有一種矩陣的方法求解$\theta$。矩陣轉換轉的頭大,公式編輯又麻煩,就不寫了.   不影響我們理解梯度下降法的原理.

隨機梯度下降法SGD

 $$\nabla L(\theta) = \begin{bmatrix}  \frac {\partial L} {\partial \theta_0} \\  \frac {\partial L} {\partial \theta_1} \\  \frac {\partial L} {\partial \theta_2} \\  … \\  \frac {\partial L}{\partial \theta_n} \\  \end{bmatrix} = \begin{bmatrix}  \sum_{i=1}^m 2(y^{(i)}-X_b^{(i)}\theta)(-1) \\  \sum_{i=1}^m 2(y^{(i)}-X_b^{(i)}\theta)(-X_1^{(i)}) \\  \sum_{i=1}^m 2(y^{(i)}-X_b^{(i)}\theta)(-X_2^{(i)}) \\  … \\  \sum_{i=1}^m 2(y^{(i)}-X_b^{(i)}\theta)(-X_n^{(i)}) \\  \end{bmatrix}$$

再來看一下這個梯度,可以看到,這個梯度的計算是與所有的樣本有關的.當X_b很大,即樣本數很多,特徵很多時,這個計算量是巨大的.

這就引申出隨機梯度下降法.在計算梯度時,只參考某一個樣本,而不參考全部樣本.

$$\nabla L(\theta) = \begin{bmatrix}  \frac {\partial L} {\partial \theta_0} \\  \frac {\partial L} {\partial \theta_1} \\  \frac {\partial L} {\partial \theta_2} \\  … \\  \frac {\partial L}{\partial \theta_n} \\  \end{bmatrix} = \begin{bmatrix}  2(y^{(i)}-X_b^{(i)}\theta)(-1) \\   2(y^{(i)}-X_b^{(i)}\theta)(-X_1^{(i)}) \\   2(y^{(i)}-X_b^{(i)}\theta)(-X_2^{(i)}) \\  … \\  2(y^{(i)}-X_b^{(i)}\theta)(-X_n^{(i)}) \\  \end{bmatrix}$$

這樣的話,將極大地提高我們每一次搜尋的速度,當然,代價就是犧牲了每一次搜尋的準確度.因為每次只參考一個樣本,導致每次搜尋的方向是隨機的.所以可能出現已經向最低點靠近了,可能下一次搜尋又折回來了,以爬山舉例,就是快到山底了,又朝上走了.  解決這個問題的方法通常是調整學習率,在梯度下降（也就是批量梯度下降）中,我們的學習率是固定的.  在隨機梯度下降中,這個值隨著搜尋次數的增加,逐漸減少. 比如取迭代次數的倒數.

小批量梯度下降法MBGD

小批量梯度下降法,兼顧了批量梯度下降和隨機梯度下降的優缺點,算是取了一個折中的方案.  每次計算梯度時,既不只參考一個樣本,也不參考全部的樣本,而是參考部分樣本. 這種最常用.

sklearn中的使用

sklearn.linear_model.SGDRegressor

　　class sklearn.linear_model.SGDRegressor(loss=’squared_loss’, penalty=’l2’, alpha=0.0001, l1_ratio=0.15, fit_intercept=True, max_iter=None, tol=None, shuffle=True, verbose=0, epsilon=0.1, random_state=None, learning_rate=’invscaling’, eta0=0.01, power_t=0.25, early_stopping=False, validation_fraction=0.1, n_iter_no_change=5, warm_start=False, average=False, n_iter=None)[source]¶

sklearn.linear_model.SGDClassifier

　　class sklearn.linear_model.SGDClassifier(loss=’hinge’, penalty=’l2’, alpha=0.0001, l1_ratio=0.15, fit_intercept=True, max_iter=None, tol=None, shuffle=True, verbose=0, epsilon=0.1, n_jobs=None, random_state=None, learning_rate=’optimal’, eta0=0.0, power_t=0.5, early_stopping=False, validation_fraction=0.1, n_iter_no_change=5, class_weight=None, warm_start=False, average=False, n_iter=None)[source]¶

使用示例：

from sklearn.preprocessing import StandardScaler

standardScaler = StandardScaler()
standardScaler.fit(X_train)
X_train_standard = standardScaler.transform(X_train)
X_test_standard = standardScaler.transform(X_test)

from sklearn.linear_model import SGDRegressor

sgd_reg = SGDRegressor()
sgd_reg.fit(X_train_standard, y_train)
sgd_reg.score(X_test_standard, y_test)

最後感慨一下,寫部落格真的很累啊,自己懂了是一回事,把懂的用語言表達給別人,讓別人也能懂,難度上升了一個級別.用文字表述出來,又要圖文並茂淺顯易懂,難度又上升了一個級別.希望自己可以堅持下去.