多元伯努利事件模型（ multi-variate Bernoulli event model）

在 GDA 中，我們要求特徵向量 x 是連續實數向量。如果 x 是離散值的話，可以考慮採用樸素貝葉斯的分類方法。
假如要分類垃圾郵件和正常郵件。
我們用一個向量x⃗ (m×1)表示一個包含m個單詞的字典。當郵件中出現字典(x⃗ )中的第i個單詞時，我們便將xi置1，否則xi=0。
舉個例子如下：

郵件中包含“a”，”buy”且字典x⃗ 中也包含它們,因此字典中的對應位置置1；
而郵件中的單詞“aardvark”，“aardwolf”，“zygmurgy”並沒有出現在字典中，這類單詞我們忽略它們；
而對於字典中未在郵件中出現過的單詞，對應的位置我們置為0。
我們的目的是為了建立模型p

(x|y).
假如字典中的單詞數為50000，這時就會有250000中可能的輸入組合，這樣我們就需要250000個參數（實際上是需要250000−1個參數,這裡的參數其實是多項式分布中的pi），引數太多，不可能用來建模。

begin-補充：多項式分佈模型（二項式分佈的擴充套件）
多項式分佈（ multinomial distribution）
某隨機實驗如果有 k 個可能結局 A1，A2，…，Ak，它們的概率分佈分別是 p1，p2，…，pk，那麼在 N 次取樣的總結果中， A1 出現n1 次，A2出現 n2 次， …， Ak 出現 nk次的這種事件的出現概率 P 有下面公式：（Xi代表出現ni次）

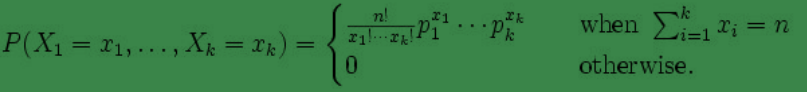
end-補充

因此，我們假設當y確定時，向量x⃗ 中的元素xi的取值(0或1)是相互獨立的。這就是樸素貝葉斯假設（Naive Bayes (NB) assumption），基於它的演算法稱為樸素貝葉斯分類器（ Naive Bayes classifier）。
注：假設中是x⃗ 中的任意兩個元素在y的條件下，是相互獨立的即：p(xi|y)=p(xi|y,xj)(i≠j)，而不是x⃗ 中的任意兩個元素是相互獨立的：p(xi)=p(xi|xj)(i≠j)。
在樸素貝葉斯假設下我們有：、

P(X|Z)=P(X|Y,Z)⟺P(X,Y|Z)=P(X|Z)P(Y|Z)

因此我們的原問題可寫為下面的形式：

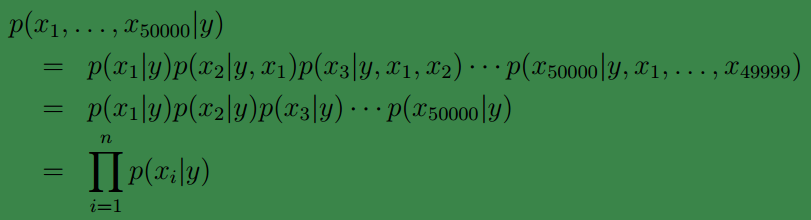
第一個等式根據概率密度鏈式法則得到，第二個等式由樸素貝葉斯假設得到。

下面給出我們模型的引數：
首先回想樸素貝葉斯公式：p(y