昨天做usaco的一道題，把遞迴函式非遞迴化看看對效率的提升，對如何轉化，做了一些嘗試。

理解遞迴過程

遞迴是函式呼叫自己本身，每呼叫一次自己，就進入一個新的堆疊幀

非遞迴化

通過觀察遞迴的過程，我們知道這是通過堆疊來實現的，那麼非遞迴化，就是
我們手動構造一個堆疊，在一次函式過程中模擬遞迴。

既然我們構造堆疊，堆疊要儲存什麼資訊？

  儲存函式的區域性變數，及執行到的語句。

堆疊的維護

 每呼叫一次函式，相對應就要push一個狀態，離開函式，就要pop

示例

簡單起見，我們首先來看看二叉樹遍歷的非遞迴化
首先，二叉樹的先序遍歷 遞迴寫法:

void
 
 preOrder(TreeNode* root)
{
    if(root==NULL)
        return;
    printf("%d ",root->val);
   preOrder(root->left);
   preOrder(root->right);
}

函式區域性變數，只有root，需要儲存在自己維護的堆疊，而執行到的位置，此處並不需要儲存，因為我們知道函式執行left後，會以right為root進入新的棧幀，那麼我們提前把root->right push進自己維護的堆疊就好了.
while迴圈每一次，就代表執行一次函式

void
 
 preOrder(TreeNode* root)
{

 stack<TreeNode*> q;
 TreeNode* tp;
 q.push(root);
 while(!q.empty())
 {
   tp = q.top();
   q.pop();
   if(tp==NULL)
     continue;
     q.push(tp->right);
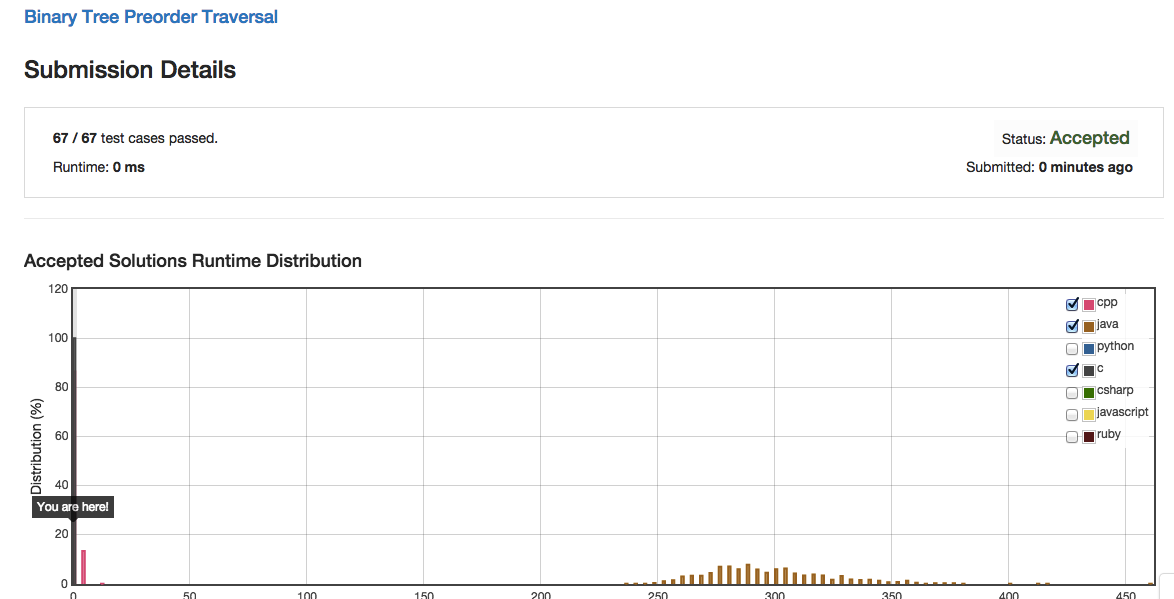
     q.push(tp->left);
 }
}

我把非遞迴的版本放進leetcode 二叉樹先序遍歷那一題進行了測試，結果如下

更復雜的遞迴函式

二叉樹的遍歷是比較簡單的遞迴函式，如果函式複雜一點，拿我之前嘗試的例子做個說明，函式的遞迴寫法如下:
這個gen函式是生成長度為level的素數，而且從右往左每減少一位得到的數仍然是素數，比如23是素數，減少一位，2仍然是素數

void gen(int level)
{
    int sum = 0;
    if(0 == level)
    {
        num[n] = '\0';
        sum = atoi(num);
        fou<<sum<<endl;
        return;
    }
    for(int i=0; i<5; ++i)
    {
        num[n-level] = sdigit[i];
        num[n-level+1] = '\0';
        sum = atoi(num);
        if(isPrime(sum))
            gen(level-1);
    }
}

函式的區域性變數，不僅有函式引數level，還有i，i代表了執行到何處，可以像之前那樣，把5個新狀態反序push進棧裡面就好了呢？
可以發現，num這個全域性變數受到了區域性變數i的影響，而在進入新的棧幀時，i的資訊沒有用到，所以不能簡單一次push 5個狀態，可以做如下處理:
增加visit變數代表是進入該函式還是返回該函式

typedef struct state
{
    state(int a,int b){l=a,i=b;}
    int l;
    int  i;
}state; //state 中l代表區域性變數lev，i代表for迴圈變數i
void noRecursive(int lev)
{
    int sum = 0;
    frame.push(state(lev,0));
    num[n-lev] = sdigit[0];
    while(!frame.empty())
    {
        state tp = frame.top();
        if(tp.l == 0)
        {
            num[n] = '\0';
            sum = atoi(num);
            fou<<sum<<endl;
            frame.pop();
            visit[tp.l][tp.i] = 0;
            continue;
        }
        if(!visit[tp.l][tp.i]){
            visit[tp.l][tp.i] = 1；
                num[n-tp.l] = sdigit[tp.i];
                num[n-tp.l+1] ='\0';
                sum = atoi(num);
                if(isPrime(sum)){
                    frame.push(state(tp.l-1,0));   
                }
        }
        else{
            frame.pop();
            visit[tp.l][tp.i] = 0;
            if(tp.i<4)
            {
                frame.push(state(tp.l,tp.i+1));
            }
        }
    }
}

而實際上，這種visit方式不好，因為需要額外的開銷，有時候區域性變數不是整數，這樣處理就不行了，而此題我們可以修改遞迴函式，使得i的資訊可以被利用，如下

void gen2(int level, int j)
{
    int sum = 0;
    if(0 == level)
    {
        num[n-1] = sdigit[j];
        num[n] = '\0';
        sum = atoi(num);
        if(isPrime(sum))
        fou<<sum<<endl;
        return;
    }
    if(level == n-1)
    num[n-level-1] = cdigit[j];
    else
    num[n-level-1] = sdigit[j];
    num[n-level] = '\0';
    sum = atoi(num);
    if(isPrime(sum))
    {
        for(int i=0; i<5; ++i)
        {
            gen2(level-1,i);
        }
    }
}

對應的非遞迴版如下：

void noRecursive2(int lev,int j)
{
    int sum = 0;
    frame.push(state(lev,j));
    num[n-lev-1] = sdigit[j];
    while(!frame.empty())
    {
        state tp = frame.top();
        if(tp.l == 0)
        {
            num[n-1] = sdigit[tp.i];
            num[n] = '\0';
            sum = atoi(num);
            if(isPrime(sum))
                fou<<sum<<endl;
            frame.pop();
            continue;
        }

        if(tp.l == n-1)
            num[n-tp.l-1] = cdigit[tp.i];
        else
            num[n-tp.l-1] = sdigit[tp.i];
        num[n-tp.l] ='\0';
        sum = atoi(num);
        frame.pop();
        if(isPrime(sum)){
            for(int i=4; i>=0; --i)
                frame.push(state(tp.l-1,i));

        }

    }

}