二叉樹遍歷(前序、中序、後序、層次、深度優先、廣度優先遍歷)
二叉樹是一種非常重要的資料結構,很多其它資料結構都是基於二叉樹的基礎演變而來的。對於二叉樹,有深度遍歷和廣度遍歷,深度遍歷有前序、中序以及後序三種遍歷方法,廣度遍歷即我們平常所說的層次遍歷。因為樹的定義本身就是遞迴定義,因此採用遞迴的方法去實現樹的三種遍歷不僅容易理解而且程式碼很簡潔,而對於廣度遍歷來說,需要其他資料結構的支撐,比如堆了。所以,對於一段程式碼來說,可讀性有時候要比程式碼本身的效率要重要的多。
四種主要的遍歷思想為:
前序遍歷:根結點 ---> 左子樹 ---> 右子樹
中序遍歷:左子樹---> 根結點 ---> 右子樹
後序遍歷:左子樹 ---> 右子樹 --->
根結點
層次遍歷:只需按層次遍歷即可
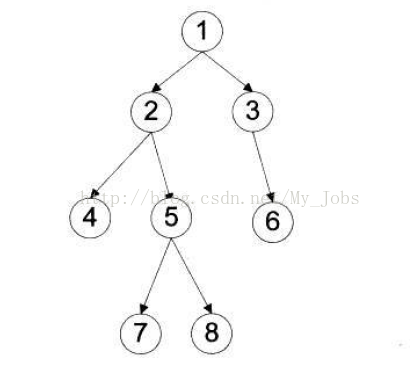
例如,求下面二叉樹的各種遍歷
前序遍歷:1 2 4 5 7 8 3 6
中序遍歷:4 2 7 5 8 1 3 6
後序遍歷:4 7 8 5 2 6 3 1
層次遍歷:1 2 3 4 5 6 7 8
一、前序遍歷
1)根據上文提到的遍歷思路:根結點 ---> 左子樹 ---> 右子樹,很容易寫出遞迴版本:
- publicvoid preOrderTraverse1(TreeNode root) {
- if (root != null) {
-
System.out.print(root.val+" ");
- preOrderTraverse1(root.left);
- preOrderTraverse1(root.right);
- }
- }
根據前序遍歷的順序,優先訪問根結點,然後在訪問左子樹和右子樹。所以,對於任意結點node,第一部分即直接訪問之,之後在判斷左子樹是否為空,不為空時即重複上面的步驟,直到其為空。若為空,則需要訪問右子樹。注意,在訪問過左孩子之後,需要反過來訪問其右孩子,所以,需要棧這種資料結構的支援。對於任意一個結點node,具體步驟如下:
a)訪問之,並把結點node入棧,當前結點置為左孩子;
b)判斷結點node是否為空,若為空,則取出棧頂結點並出棧,將右孩子置為當前結點;否則重複a)步直到當前結點為空或者棧為空(可以發現棧中的結點就是為了訪問右孩子才儲存的)
程式碼如下:
- publicvoid preOrderTraverse2(TreeNode root) {
- LinkedList<TreeNode> stack = new LinkedList<>();
- TreeNode pNode = root;
- while (pNode != null || !stack.isEmpty()) {
- if (pNode != null) {
- System.out.print(pNode.val+" ");
- stack.push(pNode);
- pNode = pNode.left;
- } else { //pNode == null && !stack.isEmpty()
- TreeNode node = stack.pop();
- pNode = node.right;
- }
- }
- }
二、中序遍歷
1)根據上文提到的遍歷思路:左子樹 ---> 根結點 ---> 右子樹,很容易寫出遞迴版本:
- publicvoid inOrderTraverse1(TreeNode root) {
- if (root != null) {
- inOrderTraverse1(root.left);
- System.out.print(root.val+" ");
- inOrderTraverse1(root.right);
- }
- }
2)非遞迴實現,有了上面前序的解釋,中序也就比較簡單了,相同的道理。只不過訪問的順序移到出棧時。程式碼如下:
- publicvoid inOrderTraverse2(TreeNode root) {
- LinkedList<TreeNode> stack = new LinkedList<>();
- TreeNode pNode = root;
- while (pNode != null || !stack.isEmpty()) {
- if (pNode != null) {
- stack.push(pNode);
- pNode = pNode.left;
- } else { //pNode == null && !stack.isEmpty()
- TreeNode node = stack.pop();
- System.out.print(node.val+" ");
- pNode = node.right;
- }
- }
- }
三、後序遍歷
1)根據上文提到的遍歷思路:左子樹 ---> 右子樹 ---> 根結點,很容易寫出遞迴版本:
- publicvoid postOrderTraverse1(TreeNode root) {
- if (root != null) {
- postOrderTraverse1(root.left);
- postOrderTraverse1(root.right);
- System.out.print(root.val+" ");
- }
- }
2)
後序遍歷的非遞迴實現是三種遍歷方式中最難的一種。因為在後序遍歷中,要保證左孩子和右孩子都已被訪問並且左孩子在右孩子前訪問才能訪問根結點,這就為流程的控制帶來了難題。下面介紹兩種思路。
第一種思路:對於任一結點P,將其入棧,然後沿其左子樹一直往下搜尋,直到搜尋到沒有左孩子的結點,此時該結點出現在棧頂,但是此時不能將其出棧並訪問,因此其右孩子還為被訪問。所以接下來按照相同的規則對其右子樹進行相同的處理,當訪問完其右孩子時,該結點又出現在棧頂,此時可以將其出棧並訪問。這樣就保證了正確的訪問順序。可以看出,在這個過程中,每個結點都兩次出現在棧頂,只有在第二次出現在棧頂時,才能訪問它。因此需要多設定一個變數標識該結點是否是第一次出現在棧頂。

void postOrder2(BinTree *root) //非遞迴後序遍歷{
stack<BTNode*> s;
BinTree *p=root;
BTNode *temp;
while(p!=NULL||!s.empty())
{
while(p!=NULL) //沿左子樹一直往下搜尋,直至出現沒有左子樹的結點 {
BTNode *btn=(BTNode *)malloc(sizeof(BTNode));
btn->btnode=p;
btn->isFirst=true;
s.push(btn);
p=p->lchild;
}
if(!s.empty())
{
temp=s.top();
s.pop();
if(temp->isFirst==true) //表示是第一次出現在棧頂 {
temp->isFirst=false;
s.push(temp);
p=temp->btnode->rchild;
}
else//第二次出現在棧頂 {
cout<<temp->btnode->data<<"";
p=NULL;
}
}
}
}

第二種思路:要保證根結點在左孩子和右孩子訪問之後才能訪問,因此對於任一結點P,先將其入棧。如果P不存在左孩子和右孩子,則可以直接訪問它;或者P存在左孩子或者右孩子,但是其左孩子和右孩子都已被訪問過了,則同樣可以直接訪問該結點。若非上述兩種情況,則將P的右孩子和左孩子依次入棧,這樣就保證了每次取棧頂元素的時候,左孩子在右孩子前面被訪問,左孩子和右孩子都在根結點前面被訪問。

void postOrder3(BinTree *root) //非遞迴後序遍歷{
stack<BinTree*> s;
BinTree *cur; //當前結點 BinTree *pre=NULL; //前一次訪問的結點 s.push(root);
while(!s.empty())
{
cur=s.top();
if((cur->lchild==NULL&&cur->rchild==NULL)||
(pre!=NULL&&(pre==cur->lchild||pre==cur->rchild)))
{
cout<<cur->data<<""; //如果當前結點沒有孩子結點或者孩子節點都已被訪問過 s.pop();
pre=cur;
}
else
{
if(cur->rchild!=NULL)
s.push(cur->rchild);
if(cur->lchild!=NULL)
s.push(cur->lchild);
}
}
}

四、層次遍歷
層次遍歷的程式碼比較簡單,只需要一個佇列即可,先在佇列中加入根結點。之後對於任意一個結點來說,在其出佇列的時候,訪問之。同時如果左孩子和右孩子有不為空的,入佇列。程式碼如下:
- publicvoid levelTraverse(TreeNode root) {
- if (root == null) {
- return;
- }
- LinkedList<TreeNode> queue = new LinkedList<>();
- queue.offer(root);
- while (!queue.isEmpty()) {
- TreeNode node = queue.poll();
- System.out.print(node.val+" ");
- if (node.left != null) {
- queue.offer(node.left);
- }
- if (node.right != null) {
- queue.offer(node.right);
- }
- }
- }
五、深度優先遍歷
其實深度遍歷就是上面的前序、中序和後序。但是為了保證與廣度優先遍歷相照應,也寫在這。程式碼也比較好理解,其實就是前序遍歷,程式碼如下:
- publicvoid depthOrderTraverse(TreeNode root) {
- if (root == null) {
- return;
- }
- LinkedList<TreeNode> stack = new LinkedList<>();
- stack.push(root);
- while (!stack.isEmpty()) {
- TreeNode node = stack.pop();
- System.out.print(node.val+" ");
- if (node.right != null) {
- stack.push(node.right);
- }
- if (node.left != null) {
- stack.push(node.left);
- }
- }
- }