在學習之前，先說一些題外話，由於博主學習模式識別沒多久，所以可能對許多問題還沒有深入的認識和正確的理解，如有不妥，還望海涵，另請各路前輩不吝賜教。

       好啦，我們開始學習吧。。

       同樣假設有樣本集：

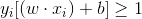
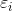
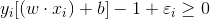
由於線性不可分，所以 不會對每一個樣本都滿足，就是說肯定會有一些小於1的樣本，對於這些樣本我們怎麼辦呢，想象一下，如果我們在不等式兩邊同時加上一個正數，是不是總會讓它不小於1，基於這樣一個想法，我們對每一個樣本引入一個非負的鬆弛因子將上述不等式變為：

         (1)

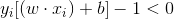
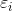
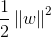
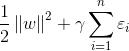
       當樣本出現錯分時，則該樣本對應的，為了保證式（1）非負，那麼必然>0，而對於那些被正確分類的樣本來說，

=0；為了保證分類的準確性和可靠性，就是在樣本不可分的情況下，我們要儘可能少的出現錯分，因此可以通過對錯分樣本對應的鬆弛因子求和來增加對錯誤的懲罰，這個求和用來來表示在整個訓練樣本集上的樣本錯分程度，當這個求和越小，表明錯分程度越小；回憶下之前的線性可分下的SVM它的目標函式，在它的基礎上我們通過增加一個懲罰項來定義不可分下的目標函式：        (2)

       在上述目標函式中，我們的目的有兩個：（1）使分類間隔儘可能大；（2）使錯分程度儘可能小；gamma表示在上述兩個目的之間的平衡引數，這個引數比較重要，值的選擇很關鍵，值太大時，說明我們對樣本錯分的容忍小，值太小，說明對錯分容忍稍大，而比較重視大間隔分類。

       基於上面兩個期望，同樣使用拉格朗日乘法來求解：

                        （3）

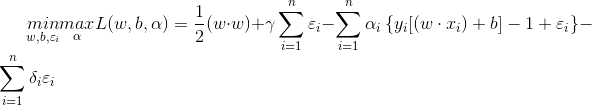
對上式泛函求導，得到下面的解：

     （4）

            （5）

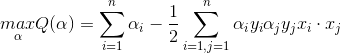
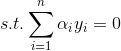
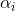
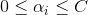
注意，這裡的跟線性可分下的不同，這裡不再只是單單的大於0就行，而是         (6)

另外得到w的解：

        （7）

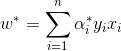
於是廣義問題的判別函式為：

       （8）

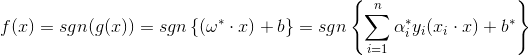
到這裡，你會發現上面幾個式子和線性可分下的完全一模一樣，唯一的不同是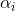多了一個上界C。

       下面，來看一看這種情況下的支援向量都有哪些樣本組成。

根據庫恩-塔克條件，泛函的鞍點出滿足以下式子：

       (9)  以及     

        (10)

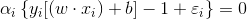
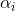
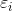
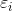
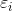
對右邊式子來說，=C時，才有>0，此時這些對應的樣本正是被錯分的樣本，而本身非負，所以其餘的樣本對應=0；

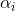
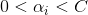
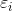
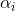
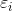
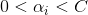
對左邊式子來說，與之前分析的一樣，{}中的那一項等於0時，才有可能使得>0，此時這些樣本又分為兩類，一類是正確分類但是位於分類邊介面上的樣本，它們滿足，=0；一類是被錯分的樣本，它們滿足=C，>0。上述兩類樣本組成了不可分下的支援向量，一類叫做邊界支援向量，一類叫做錯分支援向量。同樣b的獲得，可以通過對的樣本代入公式（9）得到，也可以進一步取平均。

      至此，可以發現，線性不可分的情況包含了可分的情況的，所以我們通常所說的SVM其實就是廣義的最優分類面形式，即無需考慮樣本可分不可分。