樹

前言：以下所有概念來自教材、演算法導論或其他權威資料，如有記錄出錯，歡迎指正

定義

• 樹是一種非線性的資料結構
• 樹是若干個結點的集合(個數>=0),是由唯一的根和若干棵互不相交的子樹組成
• 樹的結點樹可以為0，對於這種樹，我們稱為空樹
• 樹與圖的區別在於樹中沒有一個閉環

基本術語

• 結點：組成樹的元素，結點包含資料元素和指向子樹的分支
• 結點的度：結點分支數
• 樹的度：結點擁有的最大分支數
• 葉子結點：度為0的結點
• 非葉子結點：度不為0的結點，除去根節點的非葉子結點也稱為內部結點

二叉樹

• 定義：即每個結點都最多隻有兩個子結點的樹
• 
• 完全二叉樹：高度為k的二叉樹，其1~h-1層為滿結點，且其h層（葉子結點層）的節點從左至右依次排列（最多2^h-1個，最少0個）
• 
• 滿二叉樹：除最後一層外，每個結點都有左右子結點的二叉樹
• 
• 平衡二叉樹：任一結點的左右子樹的高度差絕對值不超過1，且左右子樹均為平衡二叉樹（防止樹退化成連結串列）
• 

相關演算法

二叉樹遍歷

結點本身N，結點左子樹L，結點右子樹R

• 先序遍歷：NLR
• 中序遍歷：LNR
• 後序遍歷：LRN

以先序遍歷二叉樹為例

struct TreeNode{
	int val;
	TreeNode* left;
	TreeNode* right;
}

/**
* 遞迴方式
*/
void preOrder1(TreeNode* tree)
{
	if (tree) {
		cout<<tree->val;
		preOrder1(tree->left);
		preOrder1(tree->right);
	}
} 

/**
* 非遞迴呼叫
* 使用棧來儲存遍歷過的結點
*/
void preOrder2(TreeNode* tree)
{
	if (tree == NULL) 
		cout<<"";
	stack<TreeNode*> s;
	while (tree || !s.empty()) {
		while (tree) {
			cout<<tree->val;
			s.push(tree);
			tree = tree->left;
		}

		tree = s.top();
		s.pop();
		tree = tree->right;
	}
}
 

二叉樹交換左右子樹

也有遞迴和非遞迴兩種實現方式，非遞迴利用佇列來實現

/**
* 遞迴寫法
*/
void changeNode(TreeNode* tree)
{
	if (tree == NULL) {
		return;
	}

	TreeNode* temp = tree->right;
	tree->right = tree->left;
	tree->left = temp;
	changeNode(tree->left);
	changeNode(tree->right);
}

/**
* 非遞迴
* 用佇列來實現
*/
void changeNode(TreeNode* tree)
{
	queue<TreeNode*> q;//使用佇列來記錄訪問的結點
	TreeNode* temp;
	int first = 0,last = 0;//指標來記錄訪問結點和交換結點
	q[first++] = root;
	while (first != last) {
		tree = queue[last++];
		temp = tree->left;
		tree->left = tree->right;
		tree->right = temp;
		if (tree->left != NULL) {
			queue[first++] = tree->left;
		}

		if (tree->right != NULL) {
			queue[first++] = tree->right;
		}
	}
}
 

B-Tree

• 先說明下，資料結構中有的是B-Tree和B+Tree這兩種，很多人誤解成有B-（減）樹，B樹和B+（加）樹，這是錯誤的！！！百度搜索出來的前幾篇就有這個錯誤，很容易誤導人。

• 本質：平衡m階查詢樹
• 概念： 1. B樹每個節點有K（K>0）個關鍵字（根節點除外，根節點沒有關鍵字時樹為空），結點的分支數等於關鍵字數+1，最大的分支數就是B樹的階數，因此m階的B樹中結點最多有m個分支
  2. 非根節點和葉子節點的其他節點，分支數 > (階數 / 2)，若5階B樹則非葉子節點分支數至少為3
  3. 結點內各關鍵字互不相等且按從小到大排列，下層節點內的關鍵字取值總是落在由上層節點關鍵字所劃分的區間內

對於一個m階B樹，關鍵字個數範圍 ceil(m/2) - 1 ~ m -1 (5階 則是 2 ~ 4)

查詢

多路查詢
1. 從根節點開始，若key=k[i]，查詢成功，否則根據值範圍去對應子樹查詢

插入

以關鍵字序列{1,2,6,7,11,4,8,13,10,5}為例，構建5階B樹，則一個結點最多關鍵字4個

1. 1,2,6,7組成根節點
   
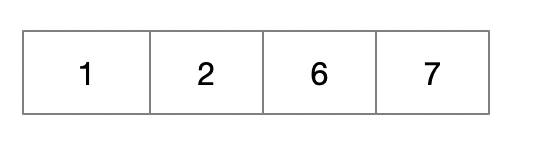
2. 插入11，超出4個關鍵字，以中心關鍵字6進行拆分
   
3. 插入4,8,13後
   
4. 再插入10，以關鍵字10進行拆分
   
5. 最後插入5

刪除

需要先找到待刪除的關鍵字，刪除中若結點關鍵字不滿足要求，則重新分配關鍵字
這是可能需要向其兄弟結點借關鍵字或者和其孩子結點進行關鍵字的交換，也可能需要進行結點的合併，其中，和當前結點的孩子進行關鍵字交換的操作可以保證刪除操作總是發生在終端結點上

B+Tree

B+樹是B樹的升級版本,就目前情況，絕大部分都已經用B+樹代替了B樹了，檔案管理、索引等等，當然，具體為什麼可以看下面的優點介紹

• 區別：B+樹非葉子節點不儲存資料，每個葉子節點指向相鄰的葉子節點
• 
• 查詢插入刪除與B樹類似
  但 B+樹提供了旋轉功能，來儘可能的減少頁的拆分
  旋轉發生在leaf Page已經滿了、但是其左右兄弟節點沒有滿的情況下

B樹與B+樹的比較

• B樹中關鍵字集合分佈在整棵樹中，葉節點中不包含任何關鍵字資訊，而B+樹關鍵字集合分佈在葉子結點中，非葉節點只是葉子結點中關鍵字的索引；
• B樹中任何一個關鍵字只出現在一個結點中，而B+樹中的關鍵字必須出現在葉節點中，也可能在非葉結點中重複出現；

例項

MySQL索引 – 見另外部落格

紅黑樹

• 本質：自平衡二叉樹

在二叉查詢樹基礎上，新增以下性質
1. 節點是紅色或黑色
2. 根節點是黑色
3. 每個為空的葉子節點是黑色的
4. 每個紅色節點的兩個子節點都是黑色
5. 從任一節點到其每個葉子節點的所有路徑都包含相同數目的黑色節點
時間複雜度為O（lgn）

左旋

右旋

插入

1. 將紅黑樹當做一顆二叉查詢樹插入
2. 將插入的節點著色為“紅色”（基於性質5）
3. 通過一系列旋轉或重新著色等操作，使之重新成為一顆紅黑樹（不會違背性質1，2，3只需考慮性質4）
4. 進行情況判斷，修正紅黑樹

刪除

同理

優點

1. 紅黑樹的插入刪除效率更高，任何不平衡都會在三次旋轉內解決
2. 二叉平衡樹比紅黑樹更為平衡，因此插入或刪除時變動頻次更高，但查詢效率也更高

如何判斷一個樹是否有環

1. 遍歷結點，標識是否遍歷過
2. 記錄每個結點到終點的座標