2. 程式人生 > >0049演算法筆記——【隨機化演算法】蒙特卡羅演算法,主元素問題,素數測試問題

0049演算法筆記——【隨機化演算法】蒙特卡羅演算法,主元素問題,素數測試問題

阿新 • • 發佈：2019-02-19

      1、蒙特卡羅演算法

基本概述

蒙特卡羅（Monte Carlo）方法，又稱隨機抽樣或統計試驗方法。傳統的經驗方法由於不能逼近真實的物理過程，很難得到滿意的結果，而蒙特卡羅方法由於能夠真實地模擬實際物理過程，故解決問題與實際非常符合，可以得到很圓滿的結果。

      在實際應用中常會遇到一些問題，不論採用確定性演算法或隨機化演算法都無法保證每次都能得到正確的解答。蒙特卡羅演算法則在一般情況下可以保證對問題的所有例項都以高概率給出正確解，但是通常無法判定一個具體解是否正確。
     設p是一個實數，且1/2<p<1。如果一個蒙特卡羅演算法對於問題的任一例項得到正確解的概率不小於p，則稱該蒙特卡羅演算法是p正確的，且稱p-1/2是該演算法的優勢。


如果對於同一例項，蒙特卡羅演算法不會給出2個不同的正確解答，則稱該蒙特卡羅演算法是一致的。
     有些蒙特卡羅演算法除了具有描述問題例項的輸入引數外，還具有描述錯誤解可接受概率的引數。這類演算法的計算時間複雜性通常由問題的例項規模以及錯誤解可接受概率的函式來描述。

原理思想

      當所要求解的問題是某種事件出現的概率，或者是某個隨機變數的期望值時，它們可以通過某種“試驗”的方法，得到這種事件出現的頻率，或者這個隨機變數的平均值，並用它們作為問題的解。這就是蒙特卡羅方法的基本思想。蒙特卡羅方法通過抓住事物運動的幾何數量和幾何特徵，利用數學方法來加以模擬，即進行一種數字模擬實驗。它是以一個概率模型為基礎，按照這個模型所描繪的過程，通過模擬實驗的結果，作為問題的近似解。

主要步驟

     蒙特卡羅解題歸結為三個主要步驟：構造或描述概率過程；實現從已知概率分佈抽樣；建立各種估計量。

 1)構造或描述概率過程： 對於本身就具有隨機性質的問題，如粒子輸運問題，主要是正確描述和模擬這個概率過程，對於本來不是隨機性質的確定性問題，比如計算定積分，就必須事先構造一個人為的概率過程，它的某些參量正好是所要求問題的解。即要將不具有隨機性質的問題轉化為隨機性質的問題。

 2)實現從已知概率分佈抽樣： 構造了概率模型以後，由於各種概率模型都可以看作是由各種各樣的概率分佈構成的，因此產生已知概率分佈的隨機變數（或隨機向量），就成為實現蒙特卡羅方法模擬實驗的基本手段，這也是蒙特卡羅方法被稱為隨機抽樣的原因。最簡單、最基本、最重要的一個概率分佈是(0,1)上的均勻分佈（或稱矩形分佈）。隨機數就是具有這種均勻分佈的隨機變數。隨機數序列就是具有這種分佈的總體的一個簡單子樣，也就是一個具有這種分佈的相互獨立的隨機變數序列。產生隨機數的問題，就是從這個分佈的抽樣問題。在計算機上，可以用物理方法產生隨機數，但價格昂貴，不能重複，使用不便。另一種方法是用數學遞推公式產生。這樣產生的序列，與真正的隨機數序列不同，所以稱為偽隨機數，或偽隨機數序列。不過，經過多種統計檢驗表明，它與真正的隨機數，或隨機數序列具有相近的性質，因此可把它作為真正的隨機數來使用。由已知分佈隨機抽樣有各種方法，與從(0,1)上均勻分佈抽樣不同，這些方法都是藉助於隨機序列來實現的，也就是說，都是以產生隨機數為前提的。由此可見，隨機數是我們實現蒙特卡羅模擬的基本工具。 建立各種估計量： 一般說來，構造了概率模型並能從中抽樣後，即實現模擬實驗後，我們就要確定一個隨機變數，作為所要求的問題的解，我們稱它為無偏估計。  


3)建立各種估計量：相當於對模擬實驗的結果進行考察和登記，從中得到問題的解。 例如：檢驗產品的正品率問題，我們可以用1表示正品，0表示次品，於是對每個產品檢驗可以定義如下的隨機變數Ti，作為正品率的估計量： 於是，在N次實驗後，正品個數為： 顯然，正品率p為： 不難看出，Ti為無偏估計。當然，還可以引入其它型別的估計，如最大似然估計，漸進有偏估計等。但是，在蒙特卡羅計算中，使用最多的是無偏估計。 用比較抽象的概率語言描述蒙特卡羅方法解題的手續如下：構造一個概率空間(W ,A,P)，其中，W 是一個事件集合，A是集合W 的子集的s 體，P是在A上建立的某個概率測度；在這個概率空間中，選取一個隨機變數q (w ),w Î W ,使得這個隨機變數的期望值 正好是所要求的解Q ，然後用q (w )的簡單子樣的算術平均值作為Q 的近似值。

      2、主元素問題

問題描述

設T[1:n]是一個含有n個元素的陣列。當|{i|T[i]=x}|>n/2時，稱元素x是陣列T的主元素。例如：陣列T[]={5,5,5,5,5,5,1,3,4,6}中，元素T[0:5]為陣列T[]的主元素。

問題求解

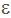
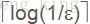
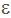
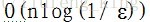
演算法隨機選擇陣列元素x,由於陣列T的非主元素個數小於n/2，所以，x不為主元素的概率小於1/2。因此判定陣列T的主元素存在性的演算法是一個偏真1/2正確的演算法。50%的錯誤概率是不可容忍的，利用重複呼叫技術將錯誤概率降低到任何可接受的範圍內。對於任何給定的>0，演算法majorityMC重複呼叫次演算法majority。它是一個偏真蒙特卡羅演算法，且其錯誤概率小於。演算法majorityMC所需的計算時間顯然是。

     演算法具體程式碼如下：

[cpp] view plaincopyprint?
  1. //隨機化演算法 蒙特卡羅演算法 主元素問題
  2. #include "stdafx.h"
  3. #include "RandomNumber.h"
  4. #include <cmath>
  5. #include <iostream>
  6. usingnamespace std;  
  7. //判定主元素的蒙特卡羅演算法
  8. template<class Type>  
  9. bool Majority(Type *T,int n)  
  10. {  
  11.     RandomNumber rnd;  
  12. int i = rnd.Random(n);  
  13.     Type x = T[i];  //隨機選擇陣列元素
  14. int k = 0;  
  15. for(int j=0; j<n; j++)  
  16.     {  
  17. if(T[j] == x)  
  18.         {  
  19.             k++;  
  20.         }  
  21.     }  
  22. return (k>n/2);  //k>n/2時，T含有主元素
  23. }  
  24. //重複k次呼叫演算法Majority
  25. template<class Type>  
  26. bool MajorityMC(Type *T,int n,double e)  
  27. {  
  28. int k = ceil(log(1/e)/log((float)2));  
  29. for(int i=1; i<=k; i++)  
  30.     {  
  31. if(Majority(T,n))  
  32.         {  
  33. returntrue;  
  34.         }  
  35.     }  
  36. returnfalse;  
  37. }  
  38. int main()  
  39. {  
  40. int n = 10;  
  41. float e = 0.001;  
  42. int a[] = {5,5,5,5,5,5,1,3,4,6};  
  43.     cout<<"陣列a的元素如下："<<endl;  
  44. for(int i=0; i<10; i++)  
  45.     {  
  46.         cout<<a[i]<<" ";  
  47.     }  
  48.     cout<<endl;  
  49.     cout<<"呼叫MajorityMC判斷陣列是否含有主元素結果是："<<MajorityMC(a,n,e)<<endl;  
  50. }  
//隨機化演算法 蒙特卡羅演算法 主元素問題
#include "stdafx.h"
#include "RandomNumber.h"
#include <cmath>
#include <iostream>
using namespace std;

//判定主元素的蒙特卡羅演算法
template<class Type>
bool Majority(Type *T,int n)
{
	RandomNumber rnd;
	int i = rnd.Random(n);

	Type x = T[i];	//隨機選擇陣列元素
	int k = 0;

	for(int j=0; j<n; j++)
	{
		if(T[j] == x)
		{
			k++;
		}
	}

	return (k>n/2);	//k>n/2時，T含有主元素
}

//重複k次呼叫演算法Majority
template<class Type>
bool MajorityMC(Type *T,int n,double e)
{
	int k = ceil(log(1/e)/log((float)2));
	for(int i=1; i<=k; i++)
	{
		if(Majority(T,n))
		{
			return true;
		}
	}
	return false;
}

int main()
{
	int n = 10;
	float e = 0.001;
	int a[] = {5,5,5,5,5,5,1,3,4,6};
	cout<<"陣列a的元素如下："<<endl;
	for(int i=0; i<10; i++)
	{
		cout<<a[i]<<" ";
	}
	cout<<endl;
	cout<<"呼叫MajorityMC判斷陣列是否含有主元素結果是："<<MajorityMC(a,n,e)<<endl;
}
    程式執行結果如圖：


     3、素數測試問題

數學原理

     Wilson定理：對於給定的正整數n，判定n是一個素數的充要條件是(n-1)! -1(mod n)。
     費爾馬小定理：如果p是一個素數，且0<a<p，則a^(p-1)(mod p)。 
     二次探測定理：如果p是一個素數，且0<x<p，則方程x^21(mod p)的解為x=1，p-1。

     Carmichael數：費爾馬小定理是素數判定的一個必要條件。滿足費爾馬小定理條件的整數n未必全是素數。有些合數也滿足費爾馬小定理的條件，這些合數稱為Carmichael數。前3個Carmichael數是561,1105，1729。Carmichael數是非常少的，在1~100000000的整數中，只有255個Carmichael數。

求a^m(mod n)的演算法

     設m的二進位制表示為bkbk-1…b1b0（bk=1）。
     例：m=41=101001(2)，bkbk-1…b1b0=101001，（k=5）。
     可以這樣來求a^m：初始C←1。
     b5=1：C←C^2(=1)，∵bk=1，做C←a*C(=a)；
     b5b4=10：C←C^2(=a^2)，∵bk-1=0，不做動作；
     b5b4b3=101：C←C^2(=a^4)，∵bk-2=1，做C←a*C(=a^5)；
     b5b4b3b2=1010：C←C^2(=a^10)，∵bk-3= b2=0，不做動作；
     b5b4b3b2b1=10100：C←C^2(=a^20)，∵bk-4= b1=0，不做動作；
     b5b4b3b2b1b0=101001：C←C^2(=a^40)，∵bk-5= b0=1，做C←a*C(=a^41)。
     最終要對am求模，而求模可以引入到計算中的每一步：
     即在求得C2及a*C之後緊接著就對這兩個值求模，然後再存入C。
     這樣做的好處是儲存在C中的最大值不超過n-1，
     於是計算的最大值不超過max{(n-1)^2,a(n-1)}。
     因此，即便am很大，求am(mod n)時也不會佔用很多空間。

     程式具體程式碼如下：

[cpp] view plaincopyprint?
  1. //隨機化演算法 蒙特卡羅演算法 素數測試問題
  2. #include "stdafx.h"
  3. #include "RandomNumber.h"
  4. #include <cmath>
  5. #include <iostream>
  6. usingnamespace std;  
  7. //計算a^p mod n,並實施對n的二次探測
  8. void power(unsigned int a,unsigned int p,unsigned int n,unsigned int &result,bool &composite)  
  9. {  
  10.     unsigned int x;  
  11. if(p == 0)  
  12.     {  
  13.         result = 1;  
  14.     }  
  15. else
  16.     {  
  17.         power(a,p/2,n,x,composite);     //遞迴計算
  18.         result = (x*x)%n;               //二次探測
  19. if((result == 1) && (x!=1) && (x!=n-1))  
  20.         {  
  21.             composite  = true;  
  22.         }  
  23. if((p%2)==1)  
  24.         {  
  25.             result = (result*a)%n;  
  26.         }  
  27.     }  
  28. }  
  29. //重複呼叫k次Prime演算法的蒙特卡羅演算法
  30. bool PrimeMC(unsigned int n,unsigned int k)  
  31. {  
  32.     RandomNumber rnd;  
  33.     unsigned int a,result;  
  34. bool composite = false;  
  35. for(int i=1; i<=k; i++)  
  36.     {  
  37.         a = rnd.Random(n-3)+2;  
  38.         power(a,n-1,n,result,composite);  
  39. if(composite || (result!=1))  
  40.         {  
  41. returnfalse;  
  42.         }  
  43.     }  
  44. returntrue;  
  45. }  
  46. int main()  
  47. {  
  48. int k = 10;  
  49. for(int i=1010;i<1025;i++)  
  50.     {  
  51.         cout<<i<<"的素數測試結果為："<<PrimeMC(i,k)<<endl;  
  52.     }  
  53. return 0;  
  54. }  
//隨機化演算法 蒙特卡羅演算法 素數測試問題
#include "stdafx.h"
#include "RandomNumber.h"
#include <cmath>
#include <iostream>
using namespace std;

//計算a^p mod n,並實施對n的二次探測
void power(unsigned int a,unsigned int p,unsigned int n,unsigned int &result,bool &composite)
{
	unsigned int x;
	if(p == 0)
	{
		result = 1;
	}
	else
	{
		power(a,p/2,n,x,composite);		//遞迴計算
		result = (x*x)%n;				//二次探測

		if((result == 1) && (x!=1) && (x!=n-1))
		{
			composite  = true;
		}

		if((p%2)==1)
		{
			result = (result*a)%n;
		}
	}
}

//重複呼叫k次Prime演算法的蒙特卡羅演算法
bool PrimeMC(unsigned int n,unsigned int k)
{
	RandomNumber rnd;
	unsigned int a,result;
	bool composite = false;

	for(int i=1; i<=k; i++)
	{
		a = rnd.Random(n-3)+2;
		power(a,n-1,n,result,composite);
		if(composite || (result!=1))
		{
			return false;
		}
	}
	return true;
}

int main()
{
	int k = 10;
	for(int i=1010;i<1025;i++)
	{
		cout<<i<<"的素數測試結果為："<<PrimeMC(i,k)<<endl;
	}
	return 0;
}
     程式執行結果如圖：


相關推薦

0049演算法筆記——【隨機化演算法】蒙特卡羅演算法,主元素問題,素數測試問題

      1、蒙特卡羅演算法 基本概述 蒙特卡羅（Monte Carlo）方法，又稱隨機抽樣或統計試驗方法。傳統的經驗方法由於不能逼近真實的物理過程，很難得到滿意的結果，而蒙特卡羅方法由於能夠真實地模擬實際物理過程，故解決問題與實際非常符合，可以得到很圓滿的結果。       在實際應用中常會遇到一些問題

0042演算法筆記——【隨機化演算法】計算π值和計算定積分

     1、計算π值 問題描述     設有一半徑為r的圓及其外切四邊形。向該正方形隨機地投擲n個點。設落入圓內的點數為k。由於所投入的點在正方形上均勻分佈，因而所投入的點落入圓內的概率為           。所以當n足夠大時，k與n之比就逼近這一概率。從而。    

0040演算法筆記——【分支限界法】批處理作業排程問題

      問題描述      給定n個作業的集合{J1,J2,…,Jn}。每個作業必須先由機器1處理，然後由機器2處理。作業Ji需要機器j的處理時間為tji。對於一個確定的作業排程，設Fji是作業i在機器j上完成處理的時間。所有作業在機器2上完成處理的時間和稱為該作業排程

0038演算法筆記——【分支限界法】旅行員售貨問題

問題描述 某售貨員要到若干城市去推銷商品，已知各城市之間的路程（旅費），他要選定一條從駐地出發，經過每個城市一遍，最後回到駐地的路線，使總的路程（總旅費）最小。     演算法思路 旅行售貨員問題的解空間可以組織成一棵樹，從樹的根結點到任一葉結點的路徑定義了圖的一條周遊

0033演算法筆記——【分支限界法】分支限界法與單源最短路徑問題

      1、分支限界法 (1)描述：採用廣度優先產生狀態空間樹的結點，並使用剪枝函式的方法稱為分枝限界法。 所謂“分支”是採用廣度優先的策略，依次生成擴充套件結點的所有分支（即：兒子結點）。所謂“限界”是在結點擴充套件過程中，計算結點的上界（或下界），邊搜尋邊減掉搜尋

演算法筆記 — 【字串】迴文串

  題目連結：http://www.codeup.cn/problem.php?cid=100000580&pid=8 題目描述 讀入一串字元，判斷是否是迴文串。“迴文串”是一個正讀和反讀都一樣的字串，比如“level”或者“noon”等等就是迴文串。 輸入

【大話資料結構】02 演算法 筆記

《大話資料結構》 ——程傑 共463頁 筆記圈點主要內容，也請多多支援大話資料結構該書作者 第 2 章 演算法 42頁_開場白 44頁_演算法定義 演算法的定義

【scikit-learn algorithm cheat sheet】【漢化版】scikit-learn演算法選擇路徑圖

英文原版連結：http://scikit-learn.org/stable/tutorial/machine_learning_map/ 看得有點累，做了個漢化版 漢化版： （有很多名詞合理地強行翻譯了一下，否則全英文的詞彙太多，不通順的時候，請看看下面的原版） 英文原

0007演算法筆記——【分治法】最接近點對問題

問題場景：在應用中，常用諸如點、圓等簡單的幾何物件代表現實世界中的實體。在涉及這些幾何物件的問題中，常需要了解其鄰域中其他幾何物件的資訊。例如，在空中交通控制問題中，若將飛機作為空間中移動的一個點來看待，則具有最大碰撞危險的2架飛機，就是這個空間中最接近的一對點。這類問題是

0020演算法筆記——【動態規劃】最優二叉搜尋樹問題

 1、問題描速： 設 S={x1, x2, ···, xn} 是一個有序集合，且x1, x2, ···, xn表示有序集合的二叉搜尋樹利用二叉樹的頂點儲存有序集中的元素，而且具有性質：儲存於每個頂點中的元素x 大於其左子樹中任一個頂點中儲存的元素，小於其右子

0008演算法筆記——【分治法】迴圈賽事日程表

問題描述：      設有n=2^k個運動員要進行網球迴圈賽。現要設計一個滿足以下要求的比賽日程表： (1)每個選手必須與其他n-1個選手各賽一次；      (2)每個選手一天只能參賽一次；      (3)迴圈賽在n-1天內結束。      請按此要求將比賽日程表

0031演算法筆記——【回溯法】旅行員售貨問題和圓排列問題

     1、旅行員售貨問題 問題描述 某售貨員要到若干城市去推銷商品，已知各城市之間的路程（旅費），他要選定一條從駐地出發，經過每個城市一遍，最後回到駐地的路線，使總的路程（總旅費）最小。     問題分析 旅行售貨員問題的解空間是一棵排列樹。對於排列樹的回溯法與生成

0021演算法筆記——【貪心演算法】貪心演算法與活動安排問題

 1、貪心演算法 (1)原理：在對問題求解時，總是做出在當前看來是最好的選擇。也就是說，不從整體最優上加以考慮，他所做出的僅是在某種意義上的區域性最優解。貪心演算法不是對所有問題都能得到整體最優解，但對範圍相當廣泛的許多問題他能產生整體最優解或者是整體最優解的近似解。

【資料探勘】FPgrowth演算法筆記

1. 提出問題 對於Apriror演算法來說，仍然受到兩種非平凡開銷的影響： 仍然需要產生大量的候選集。例如，如果有10^4個頻繁1項集，則需要產生10^7個候選頻繁2項集。 可能需要重複地掃描整個資料庫。檢索資料庫中每個事務來確定候選項集支援度的開銷會很

0014演算法筆記——【動態規劃】凸多邊形最優三角剖分

1、問題相關定義： (1)凸多邊形的三角剖分：將凸多邊形分割成互不相交的三角形的弦的集合T。 (2)最優剖分：給定凸多邊形P，以及定義在由多邊形的邊和絃組成的三角形上的權函式w。要求確定該凸多邊形的三角剖分，使得該三角剖分中諸三角形上權之和為最小。      凸多邊形三

0023演算法筆記——【貪心演算法】哈夫曼編碼問題

    1、問題描述       哈夫曼編碼是廣泛地用於資料檔案壓縮的十分有效的編碼方法。其壓縮率通常在20%～90%之間。哈夫曼編碼演算法用字元在檔案中出現的頻率表來建立一個用0，1串表示各字元的最優表示方式。一個包含100,000個字元的檔案，各字元出現頻率不同，如下表

【最小生成樹】prim演算法

演算法分析的一般步驟： 1、文字描述：如果一個演算法文字描述不清楚，就說明思路不清楚，也不可能寫好。 prim演算法是實現圖的最小生成樹。既然是圖，就假設包含n個頂點，m條邊。prim演算法是從頂點出發的，其演算法時間複雜度與頂點數目有關係。 （注意：prim演算法適合稠密圖，其時間複雜度為O(n^2)

【機器學習實戰】knn演算法手寫

首先初始化資料 def createDataSet(): group = np.array([[1.0, 1.1], [1.0, 1.0], [0.0,0.0], [0.0,0.1]]) labels = ['A', 'A', 'B', 'B']

【資料探勘】Apriori演算法

關聯分析：在大資料中尋找有趣的關係，包括頻繁項集或者關聯規則。頻繁項集是指經常一起出現的物品的集合，關聯關係暗示兩種物品之間可能存在很強的關係。這種關聯分析有什麼用呢？根據常識，經常一起出現的可能有某種關係，比如商品A和商品B在同一個頻繁項集裡，那麼可能說明購買商品A的人會選擇購買商品B，或者反

【Java面試12】常用演算法（冒泡、插入、選擇、快速）和二叉樹詳解

常用演算法（冒泡、插入、選擇、快速）和二叉樹詳解   　　同一問題可用不同演算法解決，而一個演算法的質量優劣將影響到演算法乃至程式的效率。演算法分析的目的在於選擇合適演算法和改進演算法。 　　電腦科學中，演算法的時間複雜度是一個函式，它定量描述了該演算法的執行時間。這是一個關於