## 模運算

$$
( a + b ) \% p = ( a \% p + b \% p ) \% p
$$

$$
( a * b ) \% p = ( (a \% p ) * (b \% p ) ) \% p
$$

$$
c * ( a \% p ) = ( c *a ) \% ( c *p )
$$

## 歐幾里得演算法

對於任意兩個正整數 a,b ，都有：
$$
a=kb+r (k,r∈N)
$$

所以有：
$$r=a%b$$

然後我們假設 c 是 a 和 b 的最大公約數，即
$$c=gcd(a,b)$$

然後，我們就能得到：
$$ c|a 和c|b （x|y 表示 x 能夠整除 y ， y能被x整除 , 也就是y/x是整數）$$

然後又因為上面那個式子，有：
$$r=a−kb$$
$$c|r$$
$$c=gcd(b,r)$$
即
$$gcd(a,b)=gcd(b,a\%b) $$

而且
$$gcd(a,0) = a$$

輾轉相除法函式程式碼：

```cpp
int gcd(int a,int b)//就是歐幾里得演算法函式，即輾轉相除法，求gcd(a,b)
{
int c;
while(b!=0)
{
c=a;
a=b;
b=c%b;
}
int ans=a;
return ans;
}
```

## 擴歐演算法

**例題1**
求關於$x$的同餘方程$a x \equiv 1 \pmod {b}$ 的最小正整數解.**輸入資料保證一定有解**

## 乘法逆元

**算逆元的三個方法：**

第一個方法：

```cpp
inline void exgcd(LL a,LL b)//擴充套件歐幾里得演算法求乘法逆元
{
if(b==0)
{
x=1,y=0;
return ;
}
exgcd(b,a%b);
LL k;
k=x;
x=y;
y=k-(a/b)*y;
}
```

.
.
.
.

**第二個方法:**

```cpp
int quick(int x,int p)//快速冪求乘法逆元，謹記，p是一個素數
{
int ans=1;
int d=p-2;
while(d)
{
if(d%2==1)
{
ans*=x;
ans%=p;
}
x*=x;
x%=p;
d/=2;
}
return ans;
}
```

.
.
.
.
**第三個方法：**

這裡有一個模板題目[ 題目傳送門](https://www.luogu.org/problemnew/show/P3811)

```cpp
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
long long x,y,n,f[3000010];
void work(long long n,long long p)//線性求逆元，時間複雜度O(n)
{
f[1]=1;
for(long long i=2;i<=n;i++)
{
f[i]=-(p/i)*f[p%i];
f[i]=(f[i]%p+p)%p;
}
}
int main()
{
long long a,p,b,n,i;
cin>>n>>p;
work(n,p);
for(long long i=1;i<=n;i++)
{
printf("%lld\n",f[i]);//處理出 最小正整數！！
}

return 0;
}
```

## 尤拉函式
對於正整數n,尤拉函式是小於或等於n的正整數中與n互質的數的數目，記作φ(n).

注意，尤拉函式是一個**積性函式**，只要M,N互質，就可以直接φ(MN)=φ(M)*φ(N)，線上性求1~N的尤拉函式數值的時候很有用。
另外：若a,b互質且f(ab)=f(a)*f(b),則f(x)是**積性函式**
若a,b不互質且也有f(ab)=f(a)*f(b),則f(x)是**完全積性函式**


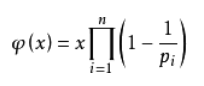
```csharp
#include<iostream>
#include<cstdio>
#include<cstring>
#define LL long long
using namespace std;

LL n;
LL phi(LL x)
{
LL ans = x;
for(int i=2;i*i<=x;i++)
{
if( x%i==0 )
{
ans = ans / i * (i-1);
while( x%i==0 ) x/=i;
}
}
if( x>1 ) ans = ans / x * (x-1);
return ans;
}

int main()
{
LL x;
cin>>n;
for(int i=1;i<=n;i++)
{
scanf("%lld",&x);
printf("%lld\n",phi(x));
}
return 0;
}
```
考慮如何用類似於篩素數的方法篩出尤拉函式。
類似於素數,可以做出如下分類討論：(設p為素數)
①$Phi(p)=p-1$
②$若已知Phi(x),pr_j能整除x: Phi(x*)=Phi(x)*p$
③$若已知Phi(x),且p不能整除x：Phi( x* pr_j )=Phi(x)*(pr_j-1)$
簡單地證明上述式子：對於①,由於$p$本身是一個素數，那麼比它小的所有數都和它互質，因此答案為$p-1$。對於②,$p$已經是x的質因子,因此我們看看尤拉函式的定義式可以的出括號相乘部分不會改變,只會把最前面的$x$變成$x*p$。對於③$p$是新加入的質因子,相當於式子前面多乘了個p,然後多加了一個括號，所以相當於原式多乘了: $p*(1-1/p)即(p-1)$。

```csharp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define LL long long
#define N 1000100
using namespace std;

LL phi[N],n,pr[N],tot = 0,ans = 0;
bool pd[N];
void getphi()
{
phi[1] = 1;
for(int i=2;i<=n;i++)
{
if( pd[i]==false )
{
pr[++tot] = i;
phi[ i ] = i-1;
}
for(int j=1;j<=tot && pr[j]*i<=n;j++)
{
LL t = i*pr[j];
pd[ t ] = true;
if( i%pr[j] == 0 )
{
phi[ t ] = phi[i] * pr[j];
break;
}
else phi[ t ] = phi[i] * (pr[j] - 1);
}
}
}
int main()
{
memset(pd,false,sizeof(pd));
cin>>n;
getphi();
for(int i=1;i<=n;i++)
{
ans += phi[i];
}
cout<<ans;
return 0;
}
```

## 數論分塊
在介紹整除分塊之前，我們先來看一道算數題：已知正整數n，求
$$
\sum_{i=1}^n \lfloor \frac{n}{i} \rfloor
$$
我們寫一個表格看一看1-20的整除是什麼樣子的
表中同樣的值會連續出現，而相同的值所劃分的區間積是整出分塊。整除的性質使得從1到n的陣列表可根據數值劃分為不同的分塊，且分塊數遠遠小於n。利用這種性質，我們如果能推匯出每個分塊具體的左右端點位置在哪，這個問題就可以快速求解出來了。

**推導公式：**

搬出例題：$$
\sum_{i=1}^n \lfloor \frac{n}{i} \rfloor
$$

假設我們已知某一個分塊的左端點$l$，要求解出該分塊的右端點$r$。設該分塊的數值為$k$，對於該分塊中的每個數$i$，有$k = \lfloor \frac{n}{l} \rfloor = \lfloor \frac{n}{i} \rfloor$即$i*k \le n$，也就是說我們找到可得使$i*k \le n$成立的**最大**的$i$的值即是我們所求的右端點$r$，因此我們可以得到下列式子:
$$
k = \lfloor \frac{n}{l} \rfloor
$$

$$
r = max(i) , i*k \le n
$$

推導可得：
$$
r = \lfloor \frac{n}{k} \rfloor = \lfloor \frac{n}{ \lfloor \frac{n}{l} \rfloor } \rfloor
$$

轉換成程式碼就是：

```cpp
ans = 0;
for(int l = 1, r; l <= n; l = r + 1)
{
r = n / (n / l);
ans += n / l * (r - l + 1);
}

```

## 簡單組合計數
**1**.$a,b$很小

![$$
\tbinom{n}{m} =
$$](https://img-blog.csdnimg.cn/8d709014e88f4d4ca381413ab5c8259e.png)

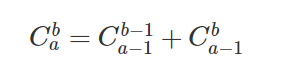
```csharp
#include<bits/stdc++.h>
#define LL long long
#define N 2010
using namespace std;
const LL MOD = 1e9+7;
LL c[N][N],n,a,b;
void init()
{
for(int i=0;i<=2000;i++)
{
for(int j=0;j<=i;j++)
{
if( !j ) c[i][j] = 1;
else c[i][j] = (c[i-1][j] + c[i-1][j-1] )%MOD;
}
}
}

int main()
{
cin>>n;
init();
while( n-- )
{
scanf("%lld %lld",&a,&b);
printf("%lld\n",c[a][b]);
}
return 0;
}
```

**2**.$a,b \leq10000$ ,求組合數模p之後的值

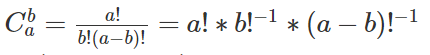
```csharp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#define N 101001
#define LL long long
using namespace std;
const LL MOD = 1e9+7;
LL quick(LL a,LL b,LL p)
{
LL ans = 1;
while( b )
{
if( b&1 ) ans = ans * a % p;
a = a*a % p;
b>>=1;
}
return ans;
}

LL n,fact[N],infact[N],a,b;

void init()
{
fact[0] = infact[0] = 1;
for(int i=1;i<N;i++)
{
fact[i] = ( fact[i-1] * i ) % MOD;
infact[i] = ( infact[i-1] * quick(i,MOD-2,MOD) ) % MOD;
}
}

int main()
{
cin>>n;
init();
while( n-- )
{
scanf("%lld %lld",&a,&b);
printf("%lld\n", fact[a] * infact[b] % MOD * infact[a-b] % MOD );
}
return 0;
}
```
**3**. $a,b \leq 10^{18}$求組合數模p的值

盧卡斯定理

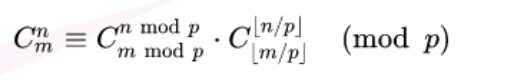
```csharp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define LL long long
using namespace std;

LL quick(LL a,LL b,LL p)
{
LL res = 1;
while( b )
{
if( b&1 ) res = res * a % p;
a = a * a % p;
b>>=1;
}
return res;
}

LL C(LL a,LL b,LL p)
{
if( b>a ) return 0;
LL ans = 1;
for(int i=1,j=a;i<=b;i++,j--)
{
ans = ans * j % p;
ans = ans * quick( i,p-2,p ) % p;
}
return ans;
}

LL lucas(LL a,LL b,LL p)
{
if( a<p && b<p ) return C(a,b,p);
return C( a%p,b%p,p ) * lucas( a/p,b/p,p )%p;
}

int main()
{
LL n,a,b,p;
cin>>n;
while( n-- )
{
scanf("%lld %lld %lld",&a,&b,&p);
printf("%lld\n",lucas(a,b,p));
}
return 0;
}
```