洛谷——P3379 【模板】最近公共祖先（LCA）

題目描述

如題，給定一棵有根多叉樹，請求出指定兩個點直接最近的公共祖先。

輸入輸出格式

輸入格式：

第一行包含三個正整數N、M、S，分別表示樹的結點個數、詢問的個數和樹根結點的序號。

接下來N-1行每行包含兩個正整數x、y，表示x結點和y結點之間有一條直接連接的邊（數據保證可以構成樹）。

接下來M行每行包含兩個正整數a、b，表示詢問a結點和b結點的最近公共祖先。

輸出格式：

輸出包含M行，每行包含一個正整數，依次為每一個詢問的結果。

輸入輸出樣例

5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5

4
4
1
4
4

說明

時空限制：1000ms,128M

數據規模：

對於30%的數據：N<=10，M<=10

對於70%的數據：N<=10000，M<=10000

對於100%的數據：N<=500000，M<=500000

樣例說明：

該樹結構如下：

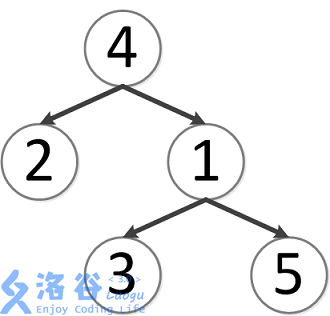
第一次詢問：2、4的最近公共祖先，故為4。

第二次詢問：3、2的最近公共祖先，故為4。

第三次詢問：3、5的最近公共祖先，故為1。

第四次詢問：1、2的最近公共祖先，故為4。

第五次詢問：4、5的最近公共祖先，故為4。

故輸出依次為4、4、1、4、4。

1.用倍增法。

代碼：

#include<vector>
#include<stdio.h>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 500001
#define maxn 123456
using namespace std;
vector<int>vec[N];
int n,x,y,fa[N][20],deep[N],m,root;
void dfs(int x)
{
    deep[x]
 
=deep[fa[x][0]]+1;
    for(int i=0;fa[x][i];i++)
      fa[x][i+1]=fa[fa[x][i]][i];
    for(int i=0;i<vec[x].size();i++)
    {
        if(!deep[vec[x][i]])
        {
            fa[vec[x][i]][0]=x;
            dfs(vec[x][i]);
         } 
    }
}
int lca(int x,int y)
{
    if(deep[x]>deep[y])
      swap(x,y);//省下後面進行分類討論，比較方便 
    for(int i=18;i>=0;i--)
    {
        if(deep[fa[y][i]]>=deep[x]) 
          y=fa[y][i];//讓一個點進行倍增，直到這兩個點的深度相同 
    }
    if(x==y) return x;//判斷兩個點在一條鏈上的情況 
    for(int i=18;i>=0;i--)
    {
        if(fa[x][i]!=fa[y][i])
        {
            y=fa[y][i];
            x=fa[x][i];
          }  
    }
    return fa[x][0];//這樣兩點的父親就是他們的最近公共祖先 
}
int main()
{
    scanf("%d%d%d",&n,&m,&root);
    for(int i=1;i<n;i++)
    {
        scanf("%d%d",&x,&y);
        vec[x].push_back(y);
        vec[y].push_back(x);
    }
    deep[root]=1;
    dfs(root);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d",&x,&y);
        printf("%d\n",lca(x,y));
    }
    return 0;
}

2.樹拋法

求lca（模板）