隨機選擇 width 證書 rom 可見 chl ctime 進一步 hostname

轉載：http://www.renfed.com/2017/02/03/https/

一、解決問題

　　HTTPS解決的是中間人攻擊

　　公網：域名解析--IP：所以中間站點搶答返回錯誤IP

　　局域網：路由器找機器是找的mac地址，路由器會向局域網類ARP廣播，找ip對應的mac地址，從而有可能產生ARP攻擊

https連接的前幾毫秒發生了什麽

2017年2月3日會編程的銀豬 7

在討論這個話題之前，先提幾個問題：

1. 為什麽說https是安全的，安全在哪裏？
2. https是使用了證書保證它的安全的麽？
3. 為什麽證書需要購買？

我們先來看https要解決什麽問題

一、 https解決什麽問題

https要解決的問題就是中間人攻擊，什麽是中間人攻擊（Man In The Middle Attack）呢？如下圖所示：

你和服務器的連接會經過一個中間人，你以為你和服務器在正常地傳輸入數據，其實這些數據都先經過了一個中間人，這個中間人可以窺探你的數據或者篡改你的數據後再發給服務器，相反也可以把服務器的數據修改了之後再發給你。而這個中間人對你是透明的，你不知道你的數據已經被人竊取或者修改了。

二、 中間人攻擊的方式

常見的有以下兩種：

1）域名汙染

由於我們訪問一個域名時需要先進行域名解析，即向DNS服務器請求某個域名的IP地址。例如taobao.com我這邊解析的IP地址為：

在經過DNS的中間鏈點可能會搶答，返回給你一個錯誤的IP地址，這個IP地址就指向中間人的機器。

2）APR欺騙

廣域網的傳輸是用的IP地址，而在局域網裏面是用的物理地址，例如路由器需要知道連接它的設備的物理地址它才可以把數據包發給你，它會通過一個ARP的廣播，向所有設備查詢某個IP地址的物理地址是多少，如下所示：

路由器發了一個廣播，詢問192.168.1.100的物理地址是多少，由於沒有人響應，所以它每隔1秒就重新發了個包。由於這個網絡上的所有機器都會收到這個包，所以這個時候就可以欺騙路由器：

上面的192.168.1.102就向路由器發了一個響應的包，告訴路由器它的物理地址。

三、https是應對中間人攻擊的唯一方式

在ssl的源碼裏面就有一段註釋：

1 2 3 4

/* cert is OK. This is the client side of an SSL connection. * Now check the name field in the cert against the desired hostname. * NB: This is our only defense against Man-In-The-Middle (MITM) attacks! */

最後一句的意思就是說使用https，是應對中間人攻擊的唯一方式。為什麽這麽說呢，這得從https連接的過程說起。

四、https連接的過程

如果對於一個外行人，可以這麽解釋：

https連接，服務器發送它的證書給瀏覽器（客戶端），瀏覽器確認證書正確，並檢查證書中對應的主機名是否正確，如果正確則雙方加密數據後發給對方，對方再進行解密，保證數據是不透明的

但是如果這個外行人比較聰明，他可能會問你瀏覽器是怎麽檢驗證書正確的，證書又是什麽東西，加密後不會被中間人破解麽?

首先證書是個什麽東西，可以在瀏覽器上面看到證書的內容，例如我們訪問谷歌，然後點擊地址欄的小鎖：

再點擊詳情->查看證書，就可以看到整個證書的完整內容：

接下來再用一個WireShark的抓包工具，抓取整個https連接的包，並分析這些包的內容。

下面以訪問淘寶為例，打開淘寶，可以在Chrome裏面看到淘寶的IP

然後打開WireShark，設定過濾條件為源IP和目的IP都為上面的IP，就可以觀察到整一個連接建立的過程：

第一步是肯定是要先建立TCP連接，這裏就不說了，我們從Client Hello開始說起：

1. Client Hello

我們在wireshark裏面觀察，將client hello裏面客戶端發給服務器的一些重要信息羅列出來

（1）使用的TLS版本是1.2，TLS有三個版本，1.0，1.1，1.2，1.2是最新的版本，https的加密就是靠的TLS安全傳輸層協議：

（2）客戶端當前的時間和一個隨機密碼串，這個時間是距Unix元年(1970.1.1)的秒數，這裏是147895117，隨機數的作用下面再提及。

（3）sessionId，會話ID，第一次連接時為0，如果有sessionId，則可以恢復會話，而不用重復握手過程：

（4）瀏覽器支持的加密組合方式：可以看到，瀏覽器一共支持22種加密組合方式，發給服務器，讓服務器選一個。具體的加密方式下文再介紹

（5）還有一個比較有趣的東西是域名：

為什麽說這個比較特別呢，因為域名是工作在應用層http裏的，而握手是發生在TLS還在傳輸層。在傳輸層裏面就把域名信息告訴服務器，好讓服務根據域名發送相應的證書。

可以說，https = http + tls，如下圖所示：

數據傳輸還是用的http，加密用的tls。tls和ssl又是什麽關系？ssl是tls的前身，ssl deprecated之後，才開始有了tls 1.0、1.1、1.2

3. Server Hello

服務器收到了Client Hello的信息後，就給瀏覽器發送了一個Server Hello的包，這個包裏面有著跟Client Hello類似的消息：

（1）時間、隨機數等，註意服務器還發送了一個Session Id給瀏覽器。

（2）服務器選中的加密方式：服務器在客戶端提供的方式裏面選擇了下面這種，這種加密方式也是目前很流行的一種方式：

4. Certificate證書

接著服務器發送一個證書的包過來：

在WireShark裏面展開證書：

服務器總共是發了三個證書，第一個叫做*.tmall.com，第二個證書叫做GlobalSign Org.，第三個叫GlobalSign Root.這三個證書是什麽關系呢？這三個證書是相互依賴的關系，在瀏覽器裏面可以看出：

tmall的證書是依賴於GlobalSign Org的證書，換句話說，GlobalSign Org的證書為tmall的證書做擔保，而根證書GlobalSign Root為GlobalSign Org做擔保，形成一條依賴鏈。明白這點很重要，從技術的角度上來說，GlobalSign為tmall的證書做簽名，只要簽名驗證正確就說明tmall的證書是合法的。

在tmall的證書裏面會指明它的上一級證書是啥：

現在來看下一個證書裏面具體有什麽內容。

除了上面提到的簽名外，每個證書還包含簽名的算法，和被簽名的證書tbsCertificate(to be signed Certificate)三部分：

這個tbsCertificate裏面有什麽東西呢？在WireShark裏面展開可以看到，裏面有申請證書時所填寫的國家、省份、城市、組織名稱：

以及證書支持的域名，可以看到taobao就在裏面：

證書的有效期，可以看到這個證書如果不續費到今年年底就要到期了：

還有證書的公鑰，GlobalSign Org的公鑰為：

我們把證書的公鑰拷貝出來，它是一串270個字節的數字，16進制為540位：

1

String publicKey = "3082010a0282010100c70e6c3f23937fcc70a59d20c30e533f7ec04ec29849ca47d523ef03348574c8a3022e465c0b7dc9889d4f8bf0f89c6c8c5535dbbff2b3eafbe356e74a46d91322ca36d59bc1a8e3964393f20cbce6f9e6e899c86348787f5736691a191d5ad1d47dc29cd47fe18012ae7aea88ea57d8ca0a0a3a1249a262197a0d24f737ebb473927b05239b12b5ceeb29dfa41402b901a5d4a69c436488def87efee3f51ee5fedca3a8e46631d94c25e918b9895909aee99d1c6d370f4a1e352028e2afd4218b01c445ad6e2b63ab926b610a4d20ed73ba7ccefe16b5db9f80f0d68b6cd908794a4f7865da92bcbe35f9b3c4f927804eff9652e60220e10773e95d2bbdb2f10203010001";

這個公鑰是由什麽組成的呢？這是由N和e組成的：

1	publicKey = (N, e)

其中N是一個大整數，由兩個質數相乘得到：

1

N = p * q

e是一個冪指數。這個就涉及到非對稱加密算法，它是針對對稱加密算法來說的。什麽是對稱加密算法呢？所謂對稱加密算法是說：會話雙方使用相同的加密解密方式，所以會話前需要先傳遞加密方式或者說是密鑰，而這個密鑰很可能會被中間人截取。所以後來才有了非對稱加密算法：加密和解密的方式不一樣，加密用的密鑰，而解密用的公鑰，公鑰是公開的，密鑰是不會傳播的，可能是保存在擁有視網膜掃描和荷槍實彈的警衛守護的機房當中。

第一個非對稱加密算法叫Diffie-Hellman密鑰交換算法，它是Diffie和Hellman發明的，後來1977年麻省理工的Rivest、Shamir 和 Adleman提出了一種新的非對稱加密算法並以他們的名字命名叫RSA。它的優點就在於：

1. 加密和解密的計算非常簡單
2. 破解十分難，只要密鑰的位數夠大，以目前的計算能力是無法破解出密鑰的

可以說，只要有計算機網絡的地方，就會有RSA。RSA加密具體是怎麽進行的呢：

5. RSA加密和解密

假設發送的信息為Hello，由於Hello的ASCII編碼為：104 101 108 108 111，所以要發送的信息為：

M = 1041010108108111

即先把要發送的文本轉成ASCII編碼或者是Unicode編碼，然後進行加密：

EM = M^e % N

就是把M作e次冪，然後除以N取余數，得到EM，EM即為加密後的信息。其中（N，e）就是上文提到的公鑰。接下來將EM發送給對方，對方收到後用自己的密鑰進行解密：

M = EM^d % N

將加密的信息作d次冪，再除以N取模，（N，d）就是對方的密鑰，這樣就能夠將EM還原為M，可以證明，只要密鑰和公鑰是一一配對的，上式一定成立。不知道密鑰的人是無法破譯的，上文已提到破解密鑰是相當困難的。

接下來回到上文提到的證書的公鑰，這是一串270個字節的數字，可以拆成兩部分N和e：

灰色的數字是用來作為標誌的。N是一個16進制為512位、二進制為2048位的大數字。普通的證書是1024位，2048位是一個很高安全級別，換算成10進制是617位，如果你能夠將這個617位的大整數拆成兩個質數相乘，就可以推導出GlobalSign的密鑰，也就是說你破解了GlobalSign的證書（但這是不可能的）。

e為65537，證書通常取的冪指數都為這個數字。

在證書裏面知道證書使用的加密算法為RSA + SHA256，SHA是一種哈希算法，可用來檢驗證書是否被篡改過：

我們將encrypted的值拷貝出來就是證書的簽名：

1

String sinature = "3ec0c71903a19be74dca101a01347ac1464c97e6e5be6d3c6677d599938a13b0db7faf2603660d4aec7056c53381b5d24c2bc0217eb78fb734874714025a0f99259c5b765c26cacff0b3c20adc9b57ea7ca63ae6a2c990837473f72c19b1d29ec575f7d7f34041a2eb744ded2dff4a2e2181979dc12f1e7511464d23d1a40b82a683df4a64d84599df0ac5999abb8946d36481cf3159b6f1e07155cf0e8125b17aba962f642e0817a896fd6c83e9e7a9aeaebfcc4adaae4df834cfeebbc95342a731f7252caa2a97796b148fd35a336476b6c23feef94d012dbfe310da3ea372043d1a396580efa7201f0f405401dff00ecd86e0dcd2f0d824b596175cb07b3d";

這個簽名是一個256個字節的數字，它是GlobalSign Org用它的密鑰對tbsCertificate做的簽名，接下來用GlobalSign Org的公鑰進行解密：

1 2 3 4 5 6 7 8

String decode = new BigInteger(signature, 16) //先轉成一個大數字 .pow(e) //再做e次冪 .mod(new BigInteger(N) ) //再模以N .toString(); System.out.println(decode);

註意在實際的計算中，不能直接e次冪，不然將是一個天文數字裏的天文數字，計算量將會非常大，需要乘一次就模一次，很快就算出來了。計算出來的結果為：

這個結果又可以拆成幾部分來看：

第一個字節是00，第一個字節要比其它字節都要小，第二個字節是01，表示這是一個私有密鑰操作，中間的ff是用來填充，加大簽名的長度，加大破解難度，最後面的64個字節就是SHA哈希的值，如果證書沒有被篡改過，那麽將tbsCertificate作一個SHA哈希，它的值應該是和簽名裏面是完全一樣的。所以接下來我們手動計算一下tbsCertificate的哈希值和簽名裏面的哈希進行對比。

這個的計算方式如下：

hash = SHA_256(DER(tbsCertificate))

註意不是將tbsCertificate直接哈希，是對它的DER編碼值進行哈希，DER是一種加密方式。DER值可以在WireShark裏面導出來，證書發過來的時候就已經被DER過了：

然後再用openssl計算它的哈希值，命令為：

openssl dgst -sha256 ~/tbsCertificate.bin

計算結果為：

即為：

bedfc063c41b62e0438bc8c0fff669de1926b5accfb487bf3fa98b8ff216d650

和上面簽名裏面的哈希值進行對比，即下面的綠色字：

可以發現：檢驗正確！這個證書沒有被篡改過，確實是tmall的證書。那麽這個時候問題來了，中間人有沒有可能既篡改了證書，還能保證哈希值是對的？首先不同的字符串被SHA256哈希後的值是一樣的概率比較小，同時由於密鑰和公鑰是一一配對的，所以中間人只能把公鑰改成它的公鑰，這個公鑰是一個p * q的整數，所以他必須得滿足兩個條件，一個是要更改成一個有意義的公鑰，另一個是整個證書的內容被哈希後的值和沒改前是一樣的，滿足這兩個條件就相當困難了。

所以我們有理由相信，只有知道了GlobalSign Org密鑰的人，才能對這個證書正確地加密。也就是說，tmall的證書確實是GobalSign頒發和簽名的，我們可以用相同的方式驗證GlobalSign Org是GlobalSign Root頒發和簽名。但是我們為什麽要相信Gloabal Sign呢？

如果上面提到的中間人不篡改證書，而是把整一個證書都換它自己的證書，假設叫HackSign，證書裏面要帶上訪問的域名，所以HackSign裏面也會帶上*.taobao.com。這個HackSign和GlobalSign有什麽區別呢？為什麽我們要相信GlobalSign，而不相信HackSign呢？

因為GlobalSign Root是瀏覽器或者操作系統自帶的證書，在火狐瀏覽器的證書列表裏面可以看到：

GlobalSign Root是Builtin的，即內置的。我們絕對相信GlobalSign Root，同時驗證了GlobalSign Org是簽名是合法的，GlobalSign Org給tmall的證書也是合法的。所以這個就是我們的信任鏈，從GlobalSign Root一直相信到了tmall。而*.taobao.com的域名已經被證書機構註冊了，所以另外的人是不能再用*.taobao.com去註冊它的證書的。

所以證書為什麽會有有效期，證書為什麽要購買，從這裏就可以知道原因了。

到這裏，你可能又會冒出來另外一個問題，既然我不能改證書，也不能換證書，那我難道不能直接克隆你的證書放到我的機器上去，因為證書是完全公開透明的，可以在瀏覽器或者wireshark裏面看到證書的完整內容。然後我再用域名汙染等技術將你訪問的域名打到我的機器上，那麽我跟你一模一樣的證書不也是合法的？證書不就沒用了？

這個問題之前也困擾我許久，為了回答這個問題，我們先繼續講解連接的過程。

上面已經說到瀏覽器已經驗證了證書是合法的，接下來：

6. 密鑰交換Key Exchange

上文提到服務器選擇的加密組合方式為：

Cipher Suite: TLS_ECDHE_RSA_WITH_AES_128_GCM_SHA256 (0xc02f)

這一串加密方式可以分成三部分：

服務器選中的密鑰交換加密方式為RSA，數據傳輸加密方式為AES，檢驗數據是否合法的算法為SHA256.

具體的密鑰交換為ECDHE_RSA，什麽叫ECDHE呢？

由於證書的密鑰和公鑰（2048位）都比較大，使用ECDH 算法最大的優勢在於，在安全性強度相同的情況下，其所需的密鑰長度較短。以 DH 演算法密鑰長度 2048 位元為例。ECDH 算法的密鑰長度僅需要 224 位元即可

所以RSA是用來驗證身份然後交換密鑰的，並不是用來加密數據的，因為它太長了，計算量太大。加密數據是用的ECDHE生成的密鑰和公鑰。

在服務器發送了它的證書給瀏覽器之後，就進行了密鑰交換Server Key Exchange和Client Key Exchange：

在WireShark裏面展開，可以看到它發給客戶端的公鑰：

這個公鑰只有65個字節，260位，和上面的270個字節的公鑰相比，已經短了很多。

同樣地，瀏覽器結合服務器發給它的隨機密碼(Server Hello)，生成它自己的主密鑰，然後發送公鑰發給服務器：

這個公鑰也是只有65個字節

雙方交換密鑰之後，瀏覽器給服務器發了一個明文的Change Cipher Spec的包，告訴服務器我已經準備好了，可以開始傳輸數據了：

同樣地，服務器也會給瀏覽器發一個Change Cipher Spec的包：

瀏覽器給服務回了個ACK，然後就開始傳輸數據：

傳輸數據是用的http傳輸的，但是數據是加密的，沒有密鑰是沒辦法解密的：

上面已經提到服務器選擇的數據傳輸加密方式為AES，AES是一種高效的加密方式，它會使用主密鑰生成另外一把密鑰，其加密過程可見維基百科。

到此，整一個連接過程就講解完了。這個時候就可以回答上文提出的證書被克隆的問題，其實答案很簡單，因為這是沒有意義的。雙方采用RSA交換公鑰，使用的公鑰和密鑰是一一配套的，所以只要證書是對的，即公鑰是對的，對方沒辦法知道配套的密鑰是多少，所以即使證書被克隆，對方收到的數據是無法解密的。所以沒有人會取偷證書，因為是沒有意義的，因為他不知道密鑰，從這個角度來說證書可以驗證身份的合法性是可以理解的

這個連接的過程大概多久呢？

四、使用https的代價

在wireshark裏面可以看到每個包的發送時間：

從最開始的Client Hello，到最後的Change Cipher Spec的包，即從4.99s到5.299秒，這個建立https連接的過程為0.3s。所以使用https是需要付出代價：

1. 建立https需要花費時間(~0.3s)
2. 數據需要加密和解密，占用更多的cpu
3. 數據加密後比原信息更大，占用更多的帶寬

五、怎樣繞過https

使用ssltrip，這個工具它的實現原理是先使用arp欺騙和用戶建立連接，然後強制將用戶訪問的https替換成http。即中間人和用戶之間是http，而和服務器還是用的https。
怎樣規避這個問題：
如果經常訪問的網站是https的，某一天突然變成了http，那麽很可能有問題，最直觀的就是瀏覽器地址欄的小鎖沒有了：

六、怎樣創建一個自簽名的證書

證書要麽買，要麽自己創建一個，可以使用openssl生成一個證書：

openssl req -x509 -nodes -sha256 -days 365 -newkey rsa:2048 -keyout test.com.key -out test.com.crt

如上，使用sha256 + rsa 2048位，有效期為365天，輸出為證書test.com.crt和密鑰test.com.key，在生成過程中它會讓你填相關的信息：

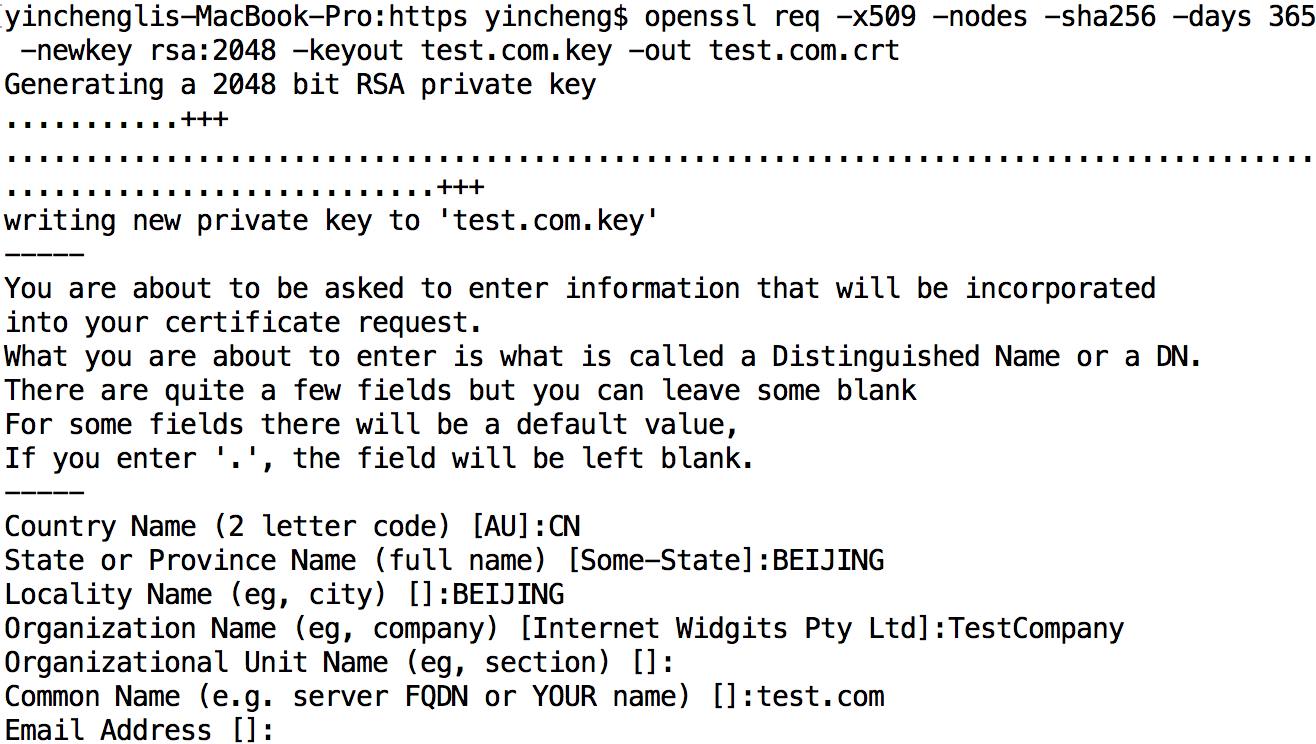
最後會生成兩個文件，一個是證書（未被簽名），另一個是密鑰：

然後把這個證書添加到瀏覽器裏面，設置為信任，瀏覽器就不會報NET::ERR_CERT_AUTHORITY_INVALID的錯誤，就可以正常使用這個證書了。

附錄：RSA加密

1977年，三位數學家Rivest、Shamir 和 Adleman 設計了一種算法，可以實現非對稱加密。這種算法用他們三個人的名字命名，叫做RSA算法。從那時直到現在，RSA算法一直是最廣為使用的"非對稱加密算法"。毫不誇張地說，只要有計算機網絡的地方，就有RSA算法。

這種算法非常可靠，密鑰越長，它就越難破解。根據已經披露的文獻，目前被破解的最長RSA密鑰是768個二進制位。也就是說，長度超過768位的密鑰，還無法破解（至少沒人公開宣布）。因此可以認為，1024位的RSA密鑰基本安全，2048位的密鑰極其安全。

下面，我就進入正題，解釋RSA算法的原理。文章共分成兩部分，今天是第一部分，介紹要用到的四個數學概念。你可以看到，RSA算法並不難，只需要一點數論知識就可以理解。

二、互質關系

如果兩個正整數，除了1以外，沒有其他公因子，我們就稱這兩個數是互質關系（coprime）。比如，15和32沒有公因子，所以它們是互質關系。這說明，不是質數也可以構成互質關系。

關於互質關系，不難得到以下結論：

　　1. 任意兩個質數構成互質關系，比如13和61。

　　2. 一個數是質數，另一個數只要不是前者的倍數，兩者就構成互質關系，比如3和10。

　　3. 如果兩個數之中，較大的那個數是質數，則兩者構成互質關系，比如97和57。

　　4. 1和任意一個自然數是都是互質關系，比如1和99。

　　5. p是大於1的整數，則p和p-1構成互質關系，比如57和56。

　　6. p是大於1的奇數，則p和p-2構成互質關系，比如17和15。

三、歐拉函數

請思考以下問題：

　　任意給定正整數n，請問在小於等於n的正整數之中，有多少個與n構成互質關系？（比如，在1到8之中，有多少個數與8構成互質關系？）

計算這個值的方法就叫做歐拉函數，以φ(n)表示。在1到8之中，與8形成互質關系的是1、3、5、7，所以 φ(n) = 4。

φ(n) 的計算方法並不復雜，但是為了得到最後那個公式，需要一步步討論。

第一種情況

如果n=1，則 φ(1) = 1 。因為1與任何數（包括自身）都構成互質關系。

第二種情況

如果n是質數，則 φ(n)=n-1 。因為質數與小於它的每一個數，都構成互質關系。比如5與1、2、3、4都構成互質關系。

第三種情況

如果n是質數的某一個次方，即 n = p^k (p為質數，k為大於等於1的整數)，則

比如 φ(8) = φ(2^3) =2^3 - 2^2 = 8 -4 = 4。

這是因為只有當一個數不包含質數p，才可能與n互質。而包含質數p的數一共有p^(k-1)個，即1×p、2×p、3×p、...、p^(k-1)×p，把它們去除，剩下的就是與n互質的數。

上面的式子還可以寫成下面的形式：

可以看出，上面的第二種情況是 k=1 時的特例。

第四種情況

如果n可以分解成兩個互質的整數之積，

　　n = p1 × p2

則

　　φ(n) = φ(p1p2) = φ(p1)φ(p2)

即積的歐拉函數等於各個因子的歐拉函數之積。比如，φ(56)=φ(8×7)=φ(8)×φ(7)=4×6=24。

這一條的證明要用到"中國剩余定理"，這裏就不展開了，只簡單說一下思路：如果a與p1互質(a<p1)，b與p2互質(b<p2)，c與p1p2互質(c<p1p2)，則c與數對 (a,b) 是一一對應關系。由於a的值有φ(p1)種可能，b的值有φ(p2)種可能，則數對 (a,b) 有φ(p1)φ(p2)種可能，而c的值有φ(p1p2)種可能，所以φ(p1p2)就等於φ(p1)φ(p2)。

第五種情況

因為任意一個大於1的正整數，都可以寫成一系列質數的積。

根據第4條的結論，得到

再根據第3條的結論，得到

也就等於

這就是歐拉函數的通用計算公式。比如，1323的歐拉函數，計算過程如下：

四、歐拉定理

歐拉函數的用處，在於歐拉定理。"歐拉定理"指的是：

如果兩個正整數a和n互質，則n的歐拉函數 φ(n) 可以讓下面的等式成立：

也就是說，a的φ(n)次方被n除的余數為1。或者說，a的φ(n)次方減去1，可以被n整除。比如，3和7互質，而7的歐拉函數φ(7)等於6，所以3的6次方（729）減去1，可以被7整除（728/7=104）。

歐拉定理的證明比較復雜，這裏就省略了。我們只要記住它的結論就行了。

歐拉定理可以大大簡化某些運算。比如，7和10互質，根據歐拉定理，

已知 φ(10) 等於4，所以馬上得到7的4倍數次方的個位數肯定是1。

因此，7的任意次方的個位數（例如7的222次方），心算就可以算出來。

歐拉定理有一個特殊情況。

假設正整數a與質數p互質，因為質數p的φ(p)等於p-1，則歐拉定理可以寫成

這就是著名的費馬小定理。它是歐拉定理的特例。

歐拉定理是RSA算法的核心。理解了這個定理，就可以理解RSA。

五、模反元素

還剩下最後一個概念：

如果兩個正整數a和n互質，那麽一定可以找到整數b，使得 ab-1 被n整除，或者說ab被n除的余數是1。

這時，b就叫做a的"模反元素"。

比如，3和11互質，那麽3的模反元素就是4，因為 (3 × 4)-1 可以被11整除。顯然，模反元素不止一個， 4加減11的整數倍都是3的模反元素 {...,-18,-7,4,15,26,...}，即如果b是a的模反元素，則 b+kn 都是a的模反元素。

歐拉定理可以用來證明模反元素必然存在。

可以看到，a的 φ(n)-1 次方，就是a的模反元素。

第一步，隨機選擇兩個不相等的質數p和q。

愛麗絲選擇了61和53。（實際應用中，這兩個質數越大，就越難破解。）

第二步，計算p和q的乘積n。

愛麗絲就把61和53相乘。

　　n = 61×53 = 3233

n的長度就是密鑰長度。3233寫成二進制是110010100001，一共有12位，所以這個密鑰就是12位。實際應用中，RSA密鑰一般是1024位，重要場合則為2048位。

第三步，計算n的歐拉函數φ(n)。

根據公式：

　　φ(n) = (p-1)(q-1)

愛麗絲算出φ(3233)等於60×52，即3120。

第四步，隨機選擇一個整數e，條件是1< e < φ(n)，且e與φ(n) 互質。

愛麗絲就在1到3120之間，隨機選擇了17。（實際應用中，常常選擇65537。）

第五步，計算e對於φ(n)的模反元素d。

所謂"模反元素"就是指有一個整數d，可以使得ed被φ(n)除的余數為1。

　　ed ≡ 1 (mod φ(n))

這個式子等價於

　　ed - 1 = kφ(n)

於是，找到模反元素d，實質上就是對下面這個二元一次方程求解。

　　ex + φ(n)y = 1

已知 e=17, φ(n)=3120，

　　17x + 3120y = 1

這個方程可以用"擴展歐幾裏得算法"求解，此處省略具體過程。總之，愛麗絲算出一組整數解為 (x,y)=(2753,-15)，即 d=2753。

至此所有計算完成。

第六步，將n和e封裝成公鑰，n和d封裝成私鑰。

在愛麗絲的例子中，n=3233，e=17，d=2753，所以公鑰就是 (3233,17)，私鑰就是（3233, 2753）。

實際應用中，公鑰和私鑰的數據都采用ASN.1格式表達（實例）。

七、RSA算法的可靠性

回顧上面的密鑰生成步驟，一共出現六個數字：

　　p
　　q
　　n
　　φ(n)
　　e
　　d

這六個數字之中，公鑰用到了兩個（n和e），其余四個數字都是不公開的。其中最關鍵的是d，因為n和d組成了私鑰，一旦d泄漏，就等於私鑰泄漏。

那麽，有無可能在已知n和e的情況下，推導出d？

　　（1）ed≡1 (mod φ(n))。只有知道e和φ(n)，才能算出d。

　　（2）φ(n)=(p-1)(q-1)。只有知道p和q，才能算出φ(n)。

　　（3）n=pq。只有將n因數分解，才能算出p和q。

結論：如果n可以被因數分解，d就可以算出，也就意味著私鑰被破解。

可是，大整數的因數分解，是一件非常困難的事情。目前，除了暴力破解，還沒有發現別的有效方法。維基百科這樣寫道：

　　"對極大整數做因數分解的難度決定了RSA算法的可靠性。換言之，對一極大整數做因數分解愈困難，RSA算法愈可靠。

　　假如有人找到一種快速因數分解的算法，那麽RSA的可靠性就會極度下降。但找到這樣的算法的可能性是非常小的。今天只有短的RSA密鑰才可能被暴力破解。到2008年為止，世界上還沒有任何可靠的攻擊RSA算法的方式。

　　只要密鑰長度足夠長，用RSA加密的信息實際上是不能被解破的。"

舉例來說，你可以對3233進行因數分解（61×53），但是你沒法對下面這個整數進行因數分解。

　　12301866845301177551304949
　　58384962720772853569595334
　　79219732245215172640050726
　　36575187452021997864693899
　　56474942774063845925192557
　　32630345373154826850791702
　　61221429134616704292143116
　　02221240479274737794080665
　　351419597459856902143413

它等於這樣兩個質數的乘積：

　　33478071698956898786044169
　　84821269081770479498371376
　　85689124313889828837938780
　　02287614711652531743087737
　　814467999489
　　　　×
　　36746043666799590428244633
　　79962795263227915816434308
　　76426760322838157396665112
　　79233373417143396810270092
　　798736308917

事實上，這大概是人類已經分解的最大整數（232個十進制位，768個二進制位）。比它更大的因數分解，還沒有被報道過，因此目前被破解的最長RSA密鑰就是768位。

八、加密和解密

有了公鑰和密鑰，就能進行加密和解密了。

（1）加密要用公鑰 (n,e)

假設鮑勃要向愛麗絲發送加密信息m，他就要用愛麗絲的公鑰 (n,e) 對m進行加密。這裏需要註意，m必須是整數（字符串可以取ascii值或unicode值），且m必須小於n。

所謂"加密"，就是算出下式的c：

　　m^e ≡ c (mod n)

愛麗絲的公鑰是 (3233, 17)，鮑勃的m假設是65，那麽可以算出下面的等式：

　　65¹⁷ ≡ 2790 (mod 3233)

於是，c等於2790，鮑勃就把2790發給了愛麗絲。

（2）解密要用私鑰(n,d)

愛麗絲拿到鮑勃發來的2790以後，就用自己的私鑰(3233, 2753) 進行解密。可以證明，下面的等式一定成立：

　　c^d ≡ m (mod n)

也就是說，c的d次方除以n的余數為m。現在，c等於2790，私鑰是(3233, 2753)，那麽，愛麗絲算出

　　2790²⁷⁵³ ≡ 65 (mod 3233)

因此，愛麗絲知道了鮑勃加密前的原文就是65。

至此，"加密--解密"的整個過程全部完成。

我們可以看到，如果不知道d，就沒有辦法從c求出m。而前面已經說過，要知道d就必須分解n，這是極難做到的，所以RSA算法保證了通信安全。

你可能會問，公鑰(n,e) 只能加密小於n的整數m，那麽如果要加密大於n的整數，該怎麽辦？有兩種解決方法：一種是把長信息分割成若幹段短消息，每段分別加密；另一種是先選擇一種"對稱性加密算法"（比如DES），用這種算法的密鑰加密信息，再用RSA公鑰加密DES密鑰。

九、私鑰解密的證明

最後，我們來證明，為什麽用私鑰解密，一定可以正確地得到m。也就是證明下面這個式子：

　　c^d ≡ m (mod n)

因為，根據加密規則

　　ｍ^e ≡ c (mod n)

於是，c可以寫成下面的形式：

　　c = m^e - kn

將c代入要我們要證明的那個解密規則：

　　(m^e - kn)^d ≡ m (mod n)

它等同於求證

　　m^ed ≡ m (mod n)

由於

　　ed ≡ 1 (mod φ(n))

所以

　　ed = hφ(n)+1

將ed代入：

　　m^hφ(n)+1 ≡ m (mod n)

接下來，分成兩種情況證明上面這個式子。

（1）m與n互質。

根據歐拉定理，此時

　　m^φ(n) ≡ 1 (mod n)

得到

　　(m^φ(n))^h × m ≡ m (mod n)

原式得到證明。

（2）m與n不是互質關系。

此時，由於n等於質數p和q的乘積，所以m必然等於kp或kq。

以 m = kp為例，考慮到這時k與q必然互質，則根據歐拉定理，下面的式子成立：

　　(kp)^q-1 ≡ 1 (mod q)

進一步得到

　　[(kp)^q-1]^h(p-1) × kp ≡ kp (mod q)

即

　　(kp)^ed ≡ kp (mod q)

將它改寫成下面的等式

　　(kp)^ed = tq + kp

這時t必然能被p整除，即 t=t‘p

　　(kp)^ed = t‘pq + kp

因為 m=kp，n=pq，所以

　　m^ed ≡ m (mod n)

原式得到證明。

網絡協議-HTTPS