[51nod1264]線段相交
阿新 • • 發佈:2017-05-28
線上 logs 一個 name img pan 線段相交 times class
給定兩個點:
typedef struct {
double x, y;
} Point;
Point A1,A2,B1,B2;
首先引入兩個實驗:
a.快速排斥實驗
設以線段A1A2和線段B1B2為對角線的矩形為M,N;
若M,N 不相交,則兩個線段顯然不相交;
所以:滿足第一個條件時:兩個線段可能相交。
b.跨立實驗
如果兩線段相交,則兩線段必然相互跨立對方.若A1A2跨立B1B2,則矢量( A1 - B1 ) 和(A2-B1)位於矢量(B2-B1)的兩側,
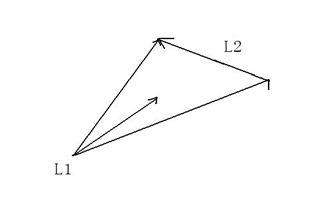
即(A1-B1) × (B2-B1) * (A2-B1) × (B2-B1)<0。
上式可改寫成(A1-B1) × (B2-B1) * (B2-B1) × (A2-A1)>0。
應該判斷兩次,即兩條線段都要為直線,判斷另一直線的兩端點是否在它兩邊,若是則兩線段相交。
若積極滿跨立實驗是不行的,如下面的情況:
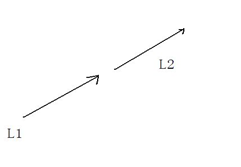
即兩條線段在同一條直線上。所以我們要同時滿足兩次跨立和快速排斥實驗。
總體分析:
當(A1-B1) × (B2-B1)=0時,說明(A1-B1)和(B2-B1)共線,但是因為已經通過快速排斥試驗,所以 A1一定在線段 B1B2上;同理,(B2-B1)×(A2-B1)=0 說明A2一定在線段B1B2上。所以判斷A1A2跨立B1B2的依據是:(A1-B1) × (B2-B1) * (B2-B1) × (A2-B1) >= 0。
同理判斷B1B2跨立A1A2的依據是:(B1-A1) × (A2-A1) * (A2-A1) × (B2-A1) >= 0。
如圖:
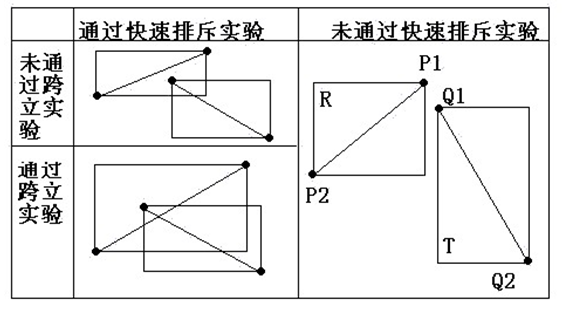
應用:
1. 判斷兩個線段相交
2. 判斷線段與直線相交
3. 判斷點在矩形內
模板題
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 struct line{ 5 double x1,y1,x2,y2; 6 }p,q;7 double cross1(line &a,line &b){ 8 return (a.x1-b.x1)*(b.y2-b.y1)-(a.y1-b.y1)*(b.x2-b.x1); 9 } 10 double cross2(line &a,line &b){ 11 return (a.x2-b.x1)*(b.y2-b.y1)-(a.y2-b.y1)*(b.x2-b.x1); 12 } 13 bool judge(line &a,line &b){ 14 if(max(a.x1,a.x2)>=min(b.x1,b.x2)&& 15 max(a.y1,a.y2)>=min(a.y1,a.y2)&& 16 max(b.x1,b.x2)>=min(a.x1,a.x2)&& 17 max(b.y1,b.y2)>=min(a.y1,a.y2)&& 18 cross1(a,b)*cross2(a,b)<=0&& 19 cross1(b,a)*cross2(b,a)<=0) 20 return true; 21 return false; 22 } 23 int main(){ 24 int t; 25 cin>>t; 26 while(t--){ 27 cin>>p.x1>>p.y1>>p.x2>>p.y2>>q.x1>>q.y1>>q.x2>>q.y2; 28 if(judge(p,q)) cout<<"Yes\n"; 29 else cout<<"No\n"; 30 } 31 }
[51nod1264]線段相交
