題目描述

小c同學認為跑步非常有趣,於是決定制作一款叫做《天天愛跑步》的遊戲。?天天愛跑步?是一個養成類遊戲,需要玩家每天按時上線,完成打卡任務。

這個遊戲的地圖可以看作一一棵包含 個結點和 條邊的樹, 每條邊連接兩個結點,且任意兩個結點存在一條路徑互相可達。樹上結點編號為從到的連續正整數。

現在有個玩家,第個玩家的起點為 ,終點為 。每天打卡任務開始時,所有玩家在第秒同時從自己的起點出發, 以每秒跑一條邊的速度, 不間斷地沿著最短路徑向著自己的終點跑去, 跑到終點後該玩家就算完成了打卡任務。 (由於地圖是一棵樹, 所以每個人的路徑是唯一的)

小C想知道遊戲的活躍度, 所以在每個結點上都放置了一個觀察員。 在結點

註意: 我們認為一個玩家到達自己的終點後該玩家就會結束遊戲, 他不能等待一 段時間後再被觀察員觀察到。 即對於把結點作為終點的玩家: 若他在第秒重到達終點,則在結點的觀察員不能觀察到該玩家;若他正好在第秒到達終點,則在結點的觀察員可以觀察到這個玩家。

輸入輸出格式

輸入格式：

第一行有兩個整數和 。其中代表樹的結點數量, 同時也是觀察員的數量, 代表玩家的數量。

接下來 行每行兩個整數和 ,表示結點 到結點 有一條邊。

接下來一行 個整數,其中第個整數為

接下來 行,每行兩個整數,和,表示一個玩家的起點和終點。

對於所有的數據,保證 。

輸出格式：

輸出1行 個整數,第個整數表示結點的觀察員可以觀察到多少人。

輸入輸出樣例

6 3
2 3
1 2 
1 4 
4 5 
4 6 
0 2 5 1 2 3 
1 5 
1 3 
2 6 

2 0 0 1 1 1 

5 3 
1 2 
2 3 
2 4 
1 5 
0 1 0 3 0 
3 1 
1 4
5 5 

1 2 1 0 1 

說明

【樣例1說明】

對於1號點，，故只有起點為1號點的玩家才會被觀察到，所以玩家1和玩家2被觀察到，共有2人被觀察到。

對於2號點，沒有玩家在第2秒時在此結點，共0人被觀察到。

對於3號點，沒有玩家在第5秒時在此結點，共0人被觀察到。

對於4號點，玩家1被觀察到，共1人被觀察到。

對於5號點，玩家1被觀察到，共1人被觀察到。

對於6號點，玩家3被觀察到，共1人被觀察到。

【子任務】

每個測試點的數據規模及特點如下表所示。 提示: 數據範圍的個位上的數字可以幫助判斷是哪一種數據類型。

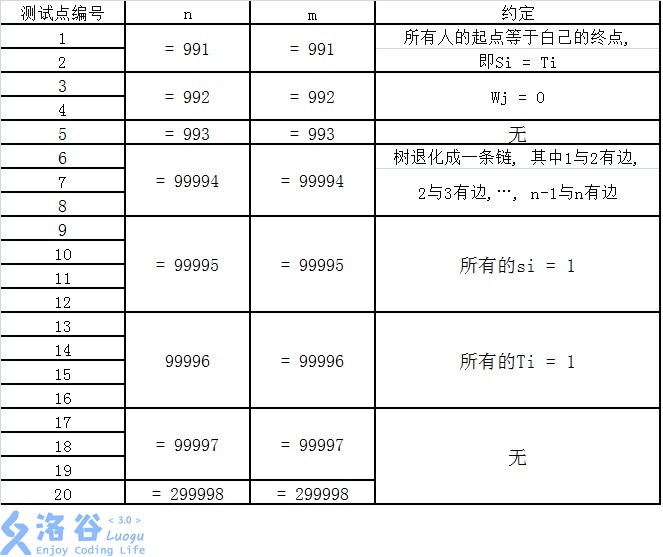
題解：

這是一道比較有趣的樹上統計題，並沒有什麽高級算法，只是思想巧妙：

用的大概是一種差分思想，是用桶實現的.（即t[i]表示深度為i的點的個數）

我們要將跑的過程轉化成 計算對一個點有貢獻的路徑的個數

於是我們可以開始討論.

我們先看一條路徑s-t：

1.先是從下往上（s-lca）跑，如果對一個點i有貢獻僅當deep[i]+w[i]=deep[s]時.

且對於每一個點，deep[i]+w[i]是定值.所以我們把所有路徑的S打上標記，

然後按照dfs序遍歷，如果一個點x有標記就把t[deep[x]]+=mark[x].

然後每一個點都做同樣的操作：ans[x]+=t[deep[i]+w[i]].

2.然後是lca-t，如果滿足L-deep[t]=w[i]-dep[i]時可產生貢獻，同樣在終點t打上++標記，

然後再回溯的回程中就會把t-lca有貢獻的點都統計完 考慮到等式兩邊都有可能產生負數，

於是就把數組偏移一個N,即所有的訪問和標記都+N

3.考慮到子樹之間 和 子樹對父節點以上節點 統計的影響 我們要在lca處打上標記，消除對父節點以上節點的影響

然後進入下一層dfs之前要保存t[i]的值，設為pre,那麽答案就為回溯以後的t[i]-pre.

4.然後調樣例的時候會發現如果lca滿足統計條件會被統計兩次，於是最後的時候需要減掉重復情況

  1 #include<iostream>
  2 #include<cstdio>
  3 #include<cmath>
  4 #include<cstring>
  5 #include<vector>
  6 using namespace std;
  7 const int N=319998,P=300001;
  8 int gi(){
  9     int str=0;char ch=getchar();
 10     while(ch>‘9‘ || ch<‘0‘)ch=getchar();
 11     while(ch>=‘0‘ && ch<=‘9‘)str=str*10+ch-‘0‘,ch=getchar();
 12     return str;
 13 }
 14 vector<int>q1[N],q2[N],q3[N];
 15 int n,m,head[N],w[N],num=0,maxdep=0;
 16 struct Lin{
 17     int next,to;
 18 }a[N*2];
 19 int Head[N],NUM=0;
 20 struct Linn{
 21     int next,to,id;
 22 }e[N*2];
 23 struct Path{
 24     int s,t,dis,lca;
 25 }q[N];
 26 int fa[N],dep[N];bool vis[N];
 27 int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
 28 void init(int x,int y){a[++num].next=head[x];a[num].to=y;head[x]=num;a[++num].next=head[y];a[num].to=x;head[y]=num;}
 29 void init2(int x,int y,int idd){e[++NUM].next=Head[x];e[NUM].to=y;e[NUM].id=idd;Head[x]=NUM;e[++NUM].next=Head[y];e[NUM].to=x,e[NUM].id=idd;Head[y]=NUM;}
 30 void tarjan(int x,int last)
 31 {
 32     int u,v,lca;
 33     vis[x]=true;
 34     if(dep[x]>maxdep)maxdep=dep[x];
 35     for(int i=head[x];i;i=a[i].next)
 36     {
 37         u=a[i].to;
 38         if(u==last)continue;
 39         dep[u]=dep[x]+1;tarjan(u,x);fa[u]=x;
 40     }
 41     for(int i=Head[x];i;i=e[i].next)
 42     {
 43         v=e[i].to;
 44         if(vis[v])
 45         {
 46             lca=find(v);
 47             q[e[i].id].lca=lca;
 48             q[e[i].id].dis=dep[v]+dep[x]-(dep[lca]<<1);
 49         }
 50     }
 51 }
 52 int t[N],ans[N],tt[N*2],mark[N];
 53 void dfs1(int x,int last)
 54 {
 55     int u,now=dep[x]+w[x],pre=0;
 56     if(now<=maxdep)pre=t[now];
 57     for(int i=head[x];i;i=a[i].next){
 58         u=a[i].to;
 59         if(u==last)continue;
 60         dfs1(u,x);
 61     }
 62     t[dep[x]]+=mark[x];
 63     if(now<=maxdep)ans[x]+=t[now]-pre;
 64     int size=q1[x].size();
 65     for(int i=0;i<size;i++)t[q1[x][i]]--;
 66 }
 67 void dfs2(int x,int last)
 68 {
 69     int u,now=w[x]-dep[x]+P,pre=tt[now];
 70     for(int i=head[x];i;i=a[i].next){
 71         u=a[i].to;
 72         if(u==last)continue;
 73         dfs2(u,x);
 74     }
 75     int size=q2[x].size();
 76     for(int i=0;i<size;i++)tt[q2[x][i]]++;
 77     ans[x]+=tt[now]-pre;
 78     size=q3[x].size();
 79     for(int i=0;i<size;i++)tt[q3[x][i]]--;
 80 }
 81 int main()
 82 {
 83     n=gi();m=gi();
 84     int x,y;
 85     for(int i=1;i<n;i++){
 86         x=gi();y=gi();
 87         init(x,y);
 88     } 
 89     for(int i=1;i<=n;i++)w[i]=gi(),fa[i]=i;
 90     for(int i=1;i<=m;i++)
 91     {
 92         q[i].s=gi();q[i].t=gi();
 93         init2(q[i].s,q[i].t,i);
 94     }
 95     dep[1]=1;
 96     tarjan(1,1);
 97     for(int i=1;i<=m;i++)
 98     {
 99         mark[q[i].s]++;
100         q1[q[i].lca].push_back(dep[q[i].s]);
101     }
102     dfs1(1,1);
103     for(int i=1;i<=m;i++)
104     {
105         q2[q[i].t].push_back(q[i].dis-dep[q[i].t]+P);
106         q3[q[i].lca].push_back(q[i].dis-dep[q[i].t]+P);
107     }
108     dfs2(1,1);
109     for(int i=1;i<=m;i++)if(w[q[i].lca]+dep[q[i].lca]==dep[q[i].s])ans[q[i].lca]--;
110     for(int i=1;i<=n;i++)printf("%d ",ans[i]);
111     return 0;
112 }

【NOIP2016】天天愛跑步