NLP —— 圖模型(二)條件隨機場(Conditional random field,CRF)
本文簡單整理了以下內容:
(一)馬爾可夫隨機場(Markov random field,無向圖模型)簡單回顧
(二)條件隨機場(Conditional random field,CRF)
這篇寫的非常淺,基於 [1] 和 [5] 梳理。感覺 [1] 的講解很適合完全不知道什麽是CRF的人來入門。如果有需要深入理解CRF的需求的話,還是應該仔細讀一下幾個英文的tutorial,比如 [4] 。
(一)馬爾可夫隨機場簡單回顧
概率圖模型(Probabilistic graphical model,PGM)是由圖表示的概率分布。概率無向圖模型(Probabilistic undirected graphical model)
設有聯合概率分布 P(V) 由無向圖 G=(V, E) 表示,圖 G 中的節點表示隨機變量,邊表示隨機變量間的依賴關系。如果聯合概率分布 P(V) 滿足成對、局部或全局馬爾可夫性,就稱此聯合概率分布為概率無向圖模型或馬爾可夫隨機場。
設有一組隨機變量 Y ,其聯合分布為 P(Y) 由無向圖 G=(V, E) 表示。圖 G 的一個節點 $v\in V$ 表示一個隨機變量 $Y_v$ ,一條邊 $e\in E$ 就表示兩個隨機變量間的依賴關系。
1. 成對馬爾可夫性(pairwise Markov property)
設無向圖 G 中的任意兩個沒有邊連接的節點 u 、v ,其他所有節點為 O ,成對馬爾可夫性指:給定 $Y_O$ 的條件下,$Y_u$ 和 $Y_v$ 條件獨立
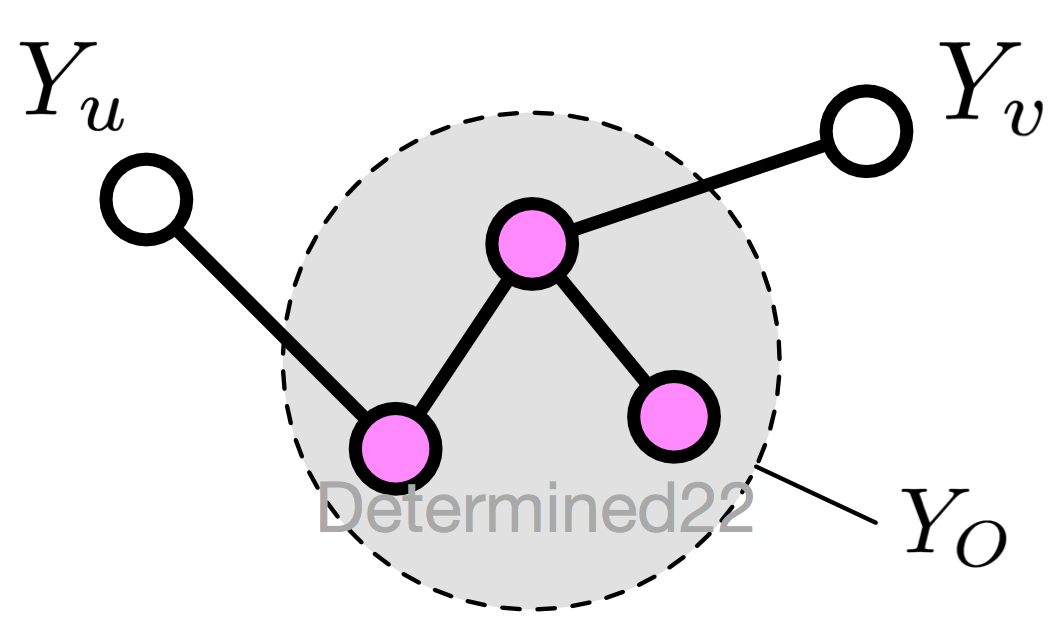
$$P(Y_u,Y_v|Y_O)=P(Y_u|Y_O)P(Y_v|Y_O)$$
2. 局部馬爾可夫性(local)
設無向圖 G 的任一節點 v ,W 是與 v 有邊相連的所有節點,O 是 v 、W 外的其他所有節點,局部馬爾可夫性指:給定 $Y_W$ 的條件下,$Y_v$ 和 $Y_O$ 條件獨立
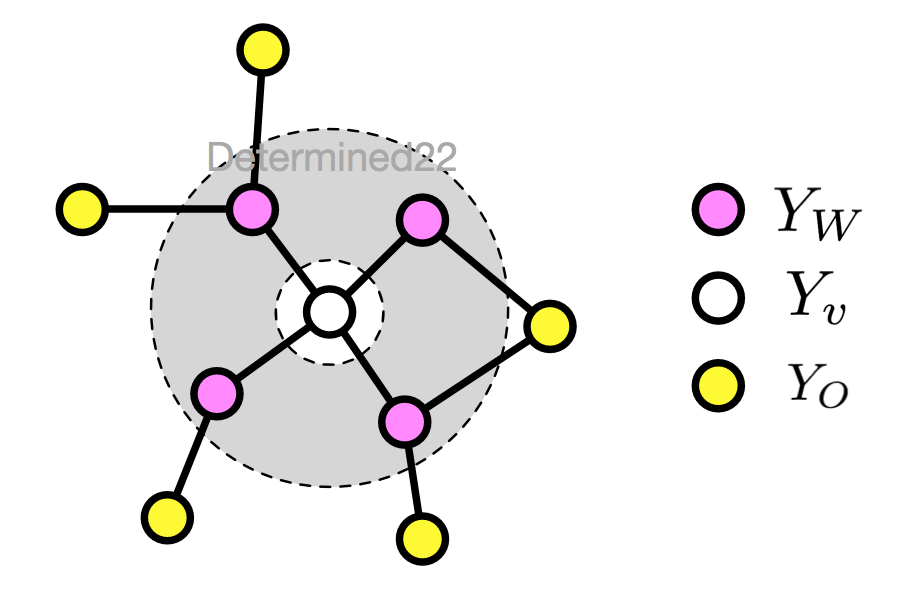
$$P(Y_v,Y_O|Y_W)=P(Y_v|Y_W)P(Y_O|Y_W)$$
當 $P(Y_O|Y_W)>0$ 時,等價於
$$P(Y_v|Y_W)=P(Y_v|Y_W,Y_O)$$
如果把等式兩邊的條件裏的 $Y_W$ 遮住,$P(Y_v)=P(Y_v|Y_O)$ 這個式子表示 $Y_v$ 和 $Y_O$ 獨立,進而可以理解這個等式為給定條件 $Y_W$ 下的獨立。
3. 全局馬爾可夫性(global)
設節點集合 A 、B 是在無向圖 G 中被節點集合 C 分開的任意節點集合,全局馬爾可夫性指:給定 $Y_C$ 的條件下,$Y_A$ 和 $Y_B$ 條件獨立
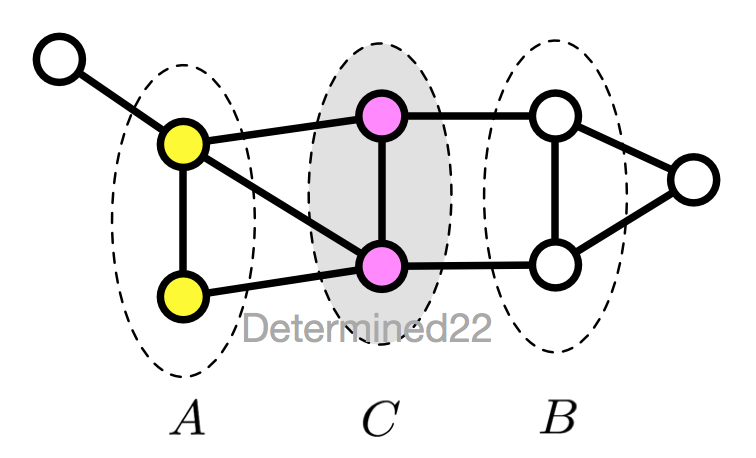
$$P(Y_A,Y_B|Y_C)=P(Y_A|Y_C)P(Y_B|Y_C)$$
這幾個定義是等價的。
4. 概率無向圖模型的因子分解
因子分解(Factorization)就是說將無向圖所描述的聯合概率分布表達為若幹個子聯合概率的乘積,從而便於模型的學習和計算。無向圖模型最大的特點就是易於因子分解。因子分解的標準定義為:
將無向圖模型的聯合概率分布表示為其最大團(maximal clique,可能不唯一)上的隨機變量的函數的乘積形式。
給定無向圖 G ,其最大團為 C ,那麽聯合概率分布 P(Y) 可以寫作圖中所有最大團 C 上的勢函數(potential function) $\psi_C(Y_C)$ 的乘積形式:
$$P(Y)=\frac1Z\prod_C\psi_C(Y_C)$$
$$Z=\sum_Y\prod_C\psi_C(Y_C)$$
其中 Z 稱為規範化因子,對 Y 的所有可能取值求和,從而保證了 P(Y) 是一個概率分布。要求勢函數嚴格正,通常定義為指數函數
$$\psi_C(Y_C)=\exp(-\mathbb E[Y_C])$$
上面的因子分解過程就是 Hammersley-Clifford 定理。
(二)條件隨機場
條件隨機場(Conditional random field,CRF)是條件概率分布模型 P(Y|X) ,表示的是給定一組輸入隨機變量 X 的條件下另一組輸出隨機變量 Y 的馬爾可夫隨機場,也就是說 CRF 的特點是假設輸出隨機變量構成馬爾可夫隨機場。
條件隨機場可被看作是最大熵馬爾可夫模型在標註問題上的推廣。
這裏介紹的是用於序列標註問題的線性鏈條件隨機場(linear chain conditional CRF),是由輸入序列來預測輸出序列的判別式模型,概率圖模型如下圖第二行中間所示。
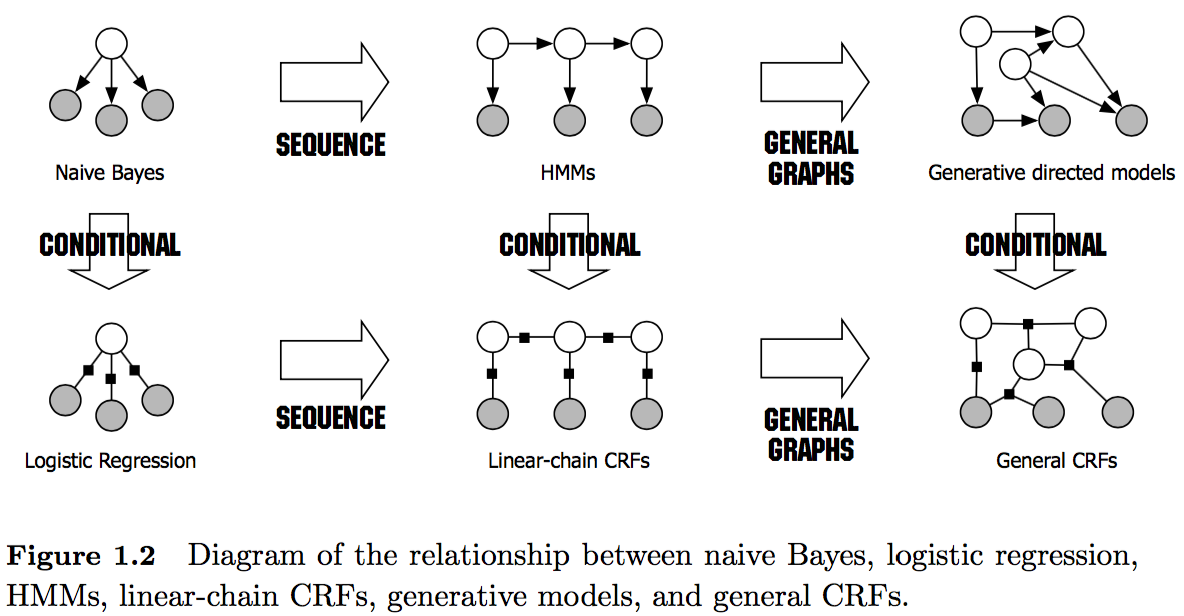
圖片來源:[4]
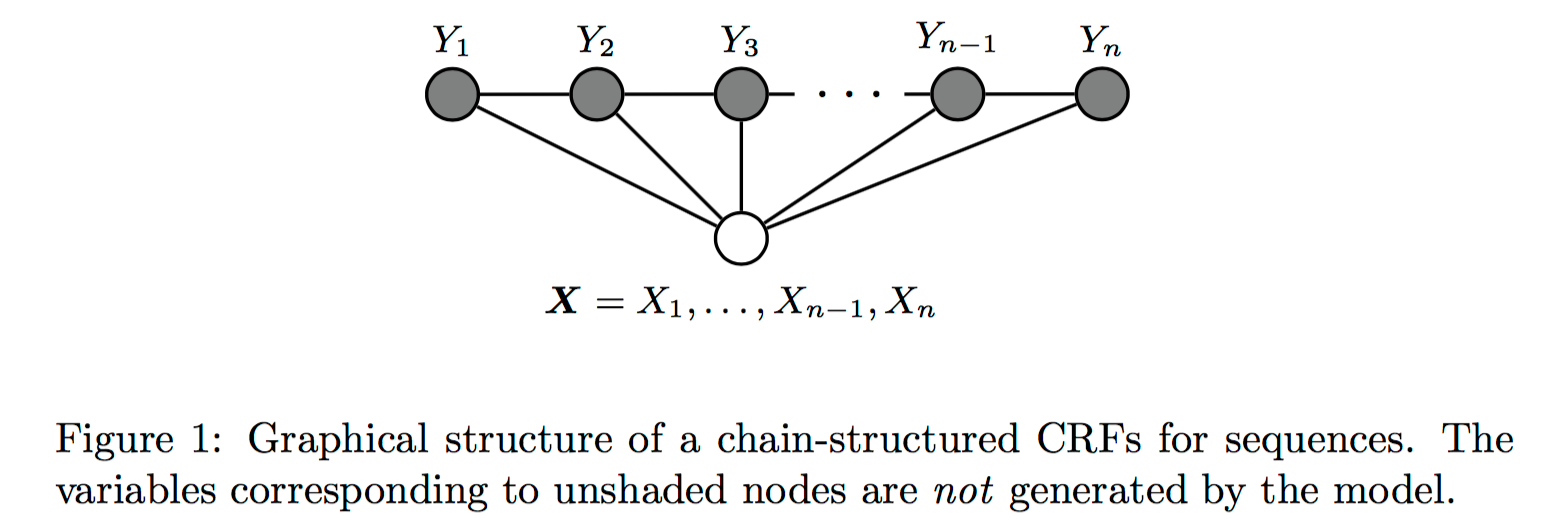
圖片來源:[3]
從問題描述上看,對於序列標註問題,X 是需要標註的觀測序列,Y 是標記序列(狀態序列)。在學習過程時,通過 MLE 或帶正則的 MLE 來訓練出模型參數;在測試過程,對於給定的觀測序列,模型需要求出條件概率最大的輸出序列。
如果隨機變量 Y 構成一個由無向圖 G=(V, E) 表示的馬爾可夫隨機場,對任意節點 $v\in V$ 都成立,即
$$P(Y_v|X,Y_w,w\not=v)=P(Y_v|X,Y_w,w\sim v)$$
對任意節點 $v$ 都成立,則稱 P(Y|X) 是條件隨機場。式中 $w\not=v$ 表示 w 是除 v 以外的所有節點,$w\sim v$ 表示 w 是與 v 相連接的所有節點。不妨把等式兩遍的相同的條件 X 都遮住,那麽式子可以用下圖示意:
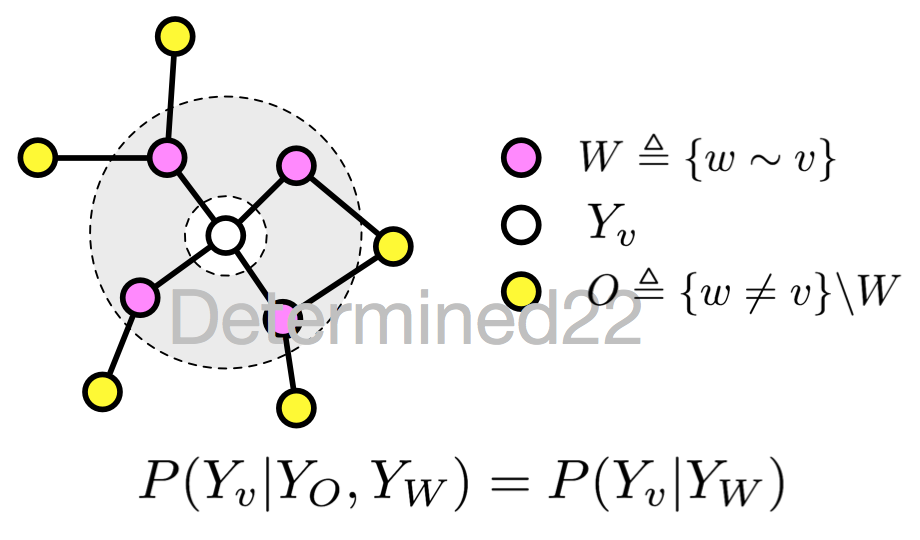
很明顯,這就是馬爾可夫隨機場的定義。
在定義中並沒有要求X和Y具有相同的結構,而在現實中,一般假設 X 和 Y 有相同的圖結構。對於線性鏈條件隨機場來說,圖 G 的每條邊都存在於狀態序列 Y 的相鄰兩個節點,最大團 C 是相鄰兩個節點的集合,X 和 Y 有相同的圖結構意味著每個 $X_i$ 都與 $Y_i$ 一一對應。
$$V=\{1,2,...,n\},\quad E=\{(i, i+1)\},\quad i=1,2,...,n-1$$
設兩組隨機變量 $X=(X_1,...,X_n),Y=(Y_1,...,Y_n)$ ,那麽線性鏈條件隨機場的定義為
$$P(Y_i|X,Y_1,...,Y_{i-1},Y_{i+1},...,Y_n)=P(Y_i|X,Y_{i-1},Y_{i+1}),\quad i=1,...,n$$
其中當 i 取 1 或 n 時只考慮單邊。
一、線性鏈條件隨機場的數學表達式
1. 線性鏈條件隨機場的參數化形式
此前我們知道,馬爾可夫隨機場可以利用最大團的函數來做因子分解。給定一個線性鏈條件隨機場 P(Y|X) ,當觀測序列為 $x=x_1x_2\cdots$ 時,狀態序列為 $y=y_1y_2\cdots$ 的概率可寫為
$$P(Y=y|x)=\frac{1}{Z(x)}\exp\biggl(\sum_k\lambda_k\sum_it_k(y_{i-1},y_i,x,i)+\sum_l\mu_l\sum_is_l(y_i,x,i)\biggr)$$
$$Z(x)=\sum_y\exp\biggl(\sum_k\lambda_k\sum_it_k(y_{i-1},y_i,x,i)+\sum_l\mu_l\sum_is_l(y_i,x,i)\biggr)$$
$Z(x)$ 作為規範化因子,是對 y 的所有可能取值求和。是不是和Softmax回歸挺像的?
這樣的對數線性模型的表達式中有幾個重要概念:
轉移特征 $t_k(y_{i-1},y_i,x,i)$ 是定義在邊上的特征函數(transition),依賴於當前位置 i 和前一位置 i-1 ;對應的權值為 $\lambda_k$ 。
狀態特征 $s_l(y_i,x,i)$ 是定義在節點上的特征函數(state),依賴於當前位置 i ;對應的權值為 $\mu_l$ 。
一般來說,特征函數的取值為 1 或 0 ,當滿足規定好的特征條件時取值為 1 ,否則為 0 。
2. 線性鏈條件隨機場的簡化形式
需要註意的是,以 $\sum_k\lambda_k\sum_it_k(y_{i-1},y_i,x,i)$ 這項為例,可以看出外面那個求和號是套著裏面的求和號的,這種雙重求和就表明了對於同一個特征(k),在各個位置(i)上都有定義。
基於此,很直覺的想法就是把同一個特征在各個位置 i 求和,形成一個全局的特征函數,也就是說讓裏面那一層求和號消失。在此之前,為了把加號的兩項合並成一項,首先將各個特征函數 t(設其共有 $K_1$ 個)、s(設共 ${K_2}$ 個)都換成統一的記號 f :
$$t_1=f_1,t_2=f_2,\cdots,t_{K_1}=f_{K_1},\quad s_1=f_{K_1+1},s_2=f_{K_1+2},\cdots,s_{K_2}=f_{K_1+K_2}$$
相應的權重同理:
$$\lambda_1=w_1,\lambda_2=w_2,\cdots,\lambda_{K_1}=w_{K_1},\quad \mu_1=w_{K_1+1},\mu_2=w_{K_1+2},\cdots,\mu_{K_2}=w_{K_1+K_2}$$
那麽就可以記為
$$f_k(y_{i-1},y_i,x,i)=\begin{cases}t_k(y_{i-1},y_i,x,i), & k=1,2,...,K_1 \\s_l(y_i,x,i), & k=K_1+l;l=1,2,...,K_2\end{cases}$$
$$w_k=\begin{cases}\lambda_k, & k=1,2,...,K_1 \\\mu_l, & k=K_1+l;l=1,2,...,K_2\end{cases}$$
然後就可以把特征在各個位置 i 求和,即
$$f_k(y,x)=\sum_{i=1}^n f_k(y_{i-1},y_i,x,i), \quad k=1,2,...,K$$
其中 $K=K_1+K_2$ 。進而可以得到簡化表示形式
$$P(Y=y|x)=\frac{1}{Z(x)}\exp\sum_{k=1}^Kw_kf_k(y,x)$$
$$Z(x)=\sum_y\exp\sum_{k=1}^Kw_kf_k(y,x)$$
如果進一步,記 $\textbf w=(w_1,w_2,...,w_K)^{\top}$ ,$F(y,x)=(f_1(y,x),...,f_K(y,x))^{\top}$ ,那麽可得內積形式:
$$P_{\textbf w}(Y=y|x)=\frac{1}{Z_{\textbf w}(x)}\exp(\textbf w^{\top}F(y,x))$$
$$Z_{\textbf w}(x)=\sum_y\exp(\textbf w^{\top}F(y,x))$$
3. 線性鏈條件隨機場的矩陣形式
這種形式依托於線性鏈條件隨機場對應的圖模型僅在兩個相鄰節點之間存在邊。在狀態序列的兩側添加兩個新的狀態 $y_0 = start$ 、$y_{n+1}=stop$ 。
這裏,引入一個新的量 $M_i(y_{i-1},y_i|x)$ :
$$M_i(y_{i-1},y_i|x)=\exp\sum_{k=1}^Kw_kf_k(y_{i-1},y_i,x,i),\quad i=1,2,...,n+1$$
首先,這個量融合了參數和特征,是一個描述模型的比較簡潔的量;其次,不難發現,這個量相比於原來的非規範化概率 $P(Y=y|x)\propto\exp\displaystyle\sum_{k=1}^Kw_kf_k(y,x)$ ,少了對位置的內層求和,換句話說這個量是針對於某個位置 i (及其前一個位置 i-1 )的。那麽,假設狀態序列的狀態存在 m 個可能的取值,對於任一位置 i = 1,2,...,n+1 ,定義一個 m 階方陣:
$$\begin{aligned}M_i(x)&=[\exp\sum_{k=1}^Kf_k(y_{i-1},y_i,x,i)]_{m\times m}\\&=[M_i(y_{i-1},y_i|x)]_{m\times m}\end{aligned}$$
因為有等式 $\displaystyle\prod_i\biggl[\exp\sum_{k=1}^Kw_kf_k(y_{i-1},y_i,x,i)\biggr]=\exp\biggl(\sum_{k=1}^Kw_k\sum_i f_k(y_{i-1},y_i,x,i)\biggr)$ 成立,所以線性鏈條件隨機場可以表述為如下的矩陣形式:
$$P_{\textbf w}(Y=y|x)=\frac{1}{Z_{\textbf w}(x)}\prod_{i=1}^{n+1}M_i(y_{i-1},y_i|x)$$
$$Z_{\textbf w}(x)=(M_1(x)M_2(x)\cdots M_{n+1}(x))_{(start,stop)}$$
其中規範化因子 $Z_{\textbf w}(x)$ 是這 n+1 個矩陣的乘積矩陣的索引為 $(start,stop)$ 的元素。 $Z_{\textbf w}(x)$ 它就等於以 start 為起點、以 stop 為終點的所有狀態路徑的非規範化概率 $\prod_{i=1}^{n+1}M_i(y_{i-1},y_i|x)$ 之和(證明略)。
上面的描述或多或少有些抽象,[1] 中給出了一個具體的例子:給定一個線性鏈條件隨機場,n = 3 ,狀態的可能取值為 5 和 7 。設 $y_0 = start = 5$ 、$y_{n+1}=stop=5$ ,且 M 矩陣在 i = 1,2,...,n+1 的值已知,求狀態序列以 start 為起點、以stop為終點的所有狀態路徑的非規範化及規範化概率。
$$M_1(x)=\begin{pmatrix}a_{01} & a_{01}\\0&0\end{pmatrix},\quad M_2(x)=\begin{pmatrix}b_{11} & b_{12}\\b_{21} & b_{22}\end{pmatrix}$$
$$M_3(x)=\begin{pmatrix}c_{11} & c_{12}\\c_{21} & c_{22}\end{pmatrix},\quad M_4(x)=\begin{pmatrix}1 & 0\\1 & 0\end{pmatrix}$$
所有可能的狀態路徑,共8條:
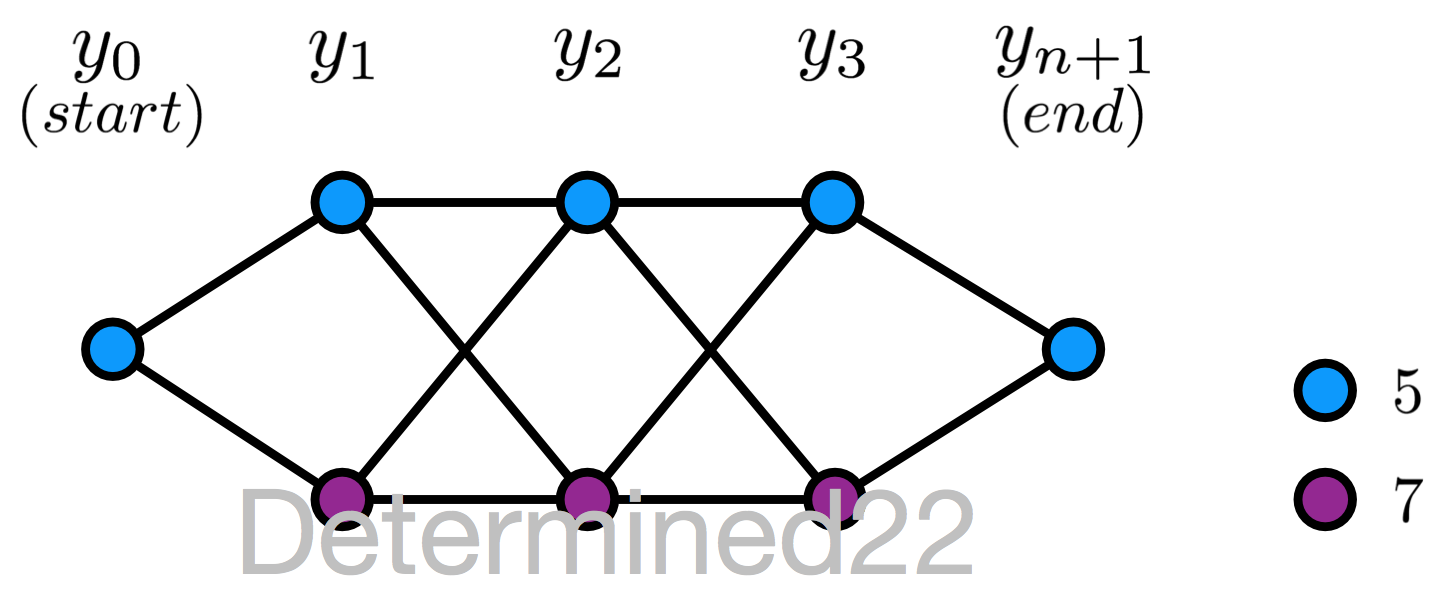
先看一下 M 矩陣的含義。以 $M_3(x)$ 為例:行索引就是當前位置(此處為3)的上一位置(此處為2)的狀態可能取值,列索引就是當前位置的狀態可能取值。

每個 M 矩陣的行/列索引都是一致的,對應於狀態的可能取值。因此,M 矩陣的每個元素值就有點Markov chain裏的“轉移概率”的意思:以 $M_3(x)$ 的 $c_{12}$ 為例,它的行索引是5,列索引是7,可以“看作”是上一位置(2)的狀態是5且當前位置(3)的狀態是7的“非規範化轉移概率”。
那麽根據公式 $P_{\textbf w}(Y=y|x)\propto\displaystyle\prod_{i=1}^{n+1}M_i(y_{i-1},y_i|x) $ ,可知狀態序列 $y_0y_1\cdots y_{4}$ 為 (5, 5, 5, 7, 5) 的非規範化概率為 $a_{01}\times b_{11}\times c_{12}\times 1$ ,其中 $a_{01}$ 是位置0的狀態為5且位置1的狀態為7的“轉移概率”,其他三項亦可以看作“轉移概率”。同理,可求得其他七條路徑的非規範化概率。
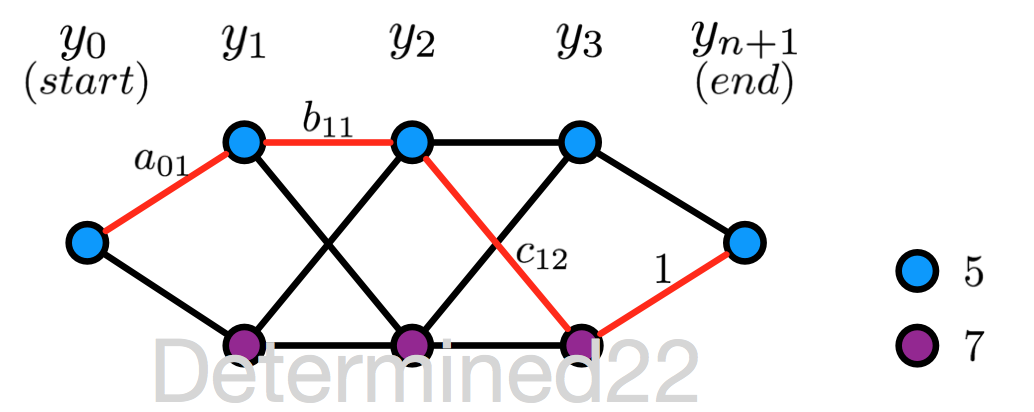
規範化因子就等於 $M_1(x)M_2(x)M_3(x)M_4(x)$ 的行索引為5、列索引為5的值,經計算,等於所有8條路徑的非規範化概率之和。
二、線性鏈條件隨機場的計算問題
與隱馬爾可夫模型類似,條件隨機場也有三個基本問題:計算問題、解碼問題和學習問題,其中前兩個問題屬於inference,第三個問題當然是learning。下面簡單介紹。
CRF的計算問題是指,給定一個條件隨機場 P(Y|X) 、觀測序列 x 和狀態序列 y ,計算 $P(Y_i=y_i|x)$ 、$P(Y_{i-1}=y_{i-1},Y_i=y_i|x)$ 以及特征函數關於分布的期望。
回顧一下HMM,當時解決這個問題使用的是前向算法/後向算法。這裏類似,對每個位置 i =0,1,...,n+1 ,定義前向向量 $\boldsymbol\alpha_i(x)$ :
$$\alpha_0(y|x)=\begin{cases}1, & y=start\\0, & otherwise\end{cases}$$
$$\alpha_i(y_i|x)=\sum_{y_{i-1}}\alpha_{i-1}(y_{i-1}|x)M_i(y_{i-1},y_i|x),\quad i=1,2,...,n+1$$
$\alpha_i(y_i|x)$ 的含義是在位置 i 的標記 $Y_i=y_i$ 且從起始位置到位置 i 的局部標記序列的非規範化概率,這個遞推式子可以直觀地把 $M_i(y_{i-1},y_i|x)$ 理解為“轉移概率”,求和號表示對 $y_{i-1}$ 的所有可能取值求和。寫成矩陣的形式就是下式
$$\boldsymbol\alpha_i^{\top}(x)=\boldsymbol\alpha_{i-1}^{\top}(x)M_i(x)$$
這裏的 $\boldsymbol\alpha_i(x)$ 是 m 維列向量,因為每個位置的標記都有 m 種可能取值,每一個維度都對應一個 $\alpha_i(y_i|x)$ 。
類似地,可以定義後向向量 $\boldsymbol\beta_i(x)$ :
$$\alpha_{n+1}(y_{n+1}|x)=\begin{cases}1, & y_{n+1}=stop\\0, & otherwise\end{cases}$$
$$\beta_i(y_i|x)=\sum_{y_{i+1}}M_{i+1}(y_{i},y_{i+1}|x)\alpha_{i+1}(y_{i+1}|x),\quad i=0,1,...,n$$
$\beta_i(y_i|x)$ 的含義是在位置 i 的標記 $Y_i=y_i$ 且從位置 i+1 到位置 n 的局部標記序列的非規範化概率。寫成矩陣的形式就是
$$\boldsymbol\beta_i^{\top}(x)=M_{i+1}(x)\boldsymbol\beta_{i+1}(x)$$
另外,規範化因子 $Z(x)=\boldsymbol\alpha^{\top}_n(x)\boldsymbol 1=\boldsymbol 1^{\top}\boldsymbol\beta_1(x)$ 。
1. 概率值的計算
給定一個CRF模型,那麽 $P(Y_i=y_i|x)$ 、$P(Y_{i-1}=y_{i-1},Y_i=y_i|x)$ 可以利用前向向量和後向向量計算為
$$P(Y_i=y_i|x)=\frac{\alpha_i(y_i|x)\beta_i(y_i|x)}{Z(x)}$$
$$P(Y_{i-1}=y_{i-1},Y_i=y_i|x)=\frac{\alpha_{i-1}(y_{i-1}|x)M_i(y_{i-1},y_i|x)\beta_i(y_i|x)}{Z(x)}$$
2. 期望值的計算
(1)特征函數 $f_k$ 關於條件分布 P(Y|X) 的期望:
$$\begin{aligned}\mathbb E_{P(Y|x)}[f_k]&=\sum_{y}P(Y=y|x)f_k(y,x)\\&=\sum_{y}P(Y=y|x)\sum_{i=1}^{n+1} f_k(y_{i-1},y_i,x,i)\\&=\sum_{i=1}^{n+1}\sum_{y_{i-1}y_i}f_k(y_{i-1},y_i,x,i)P(Y_{i-1}=y_{i-1},Y_i=y_i|x)\\&=\sum_{i=1}^{n+1}\sum_{y_{i-1}y_i}f_k(y_{i-1},y_i,x,i)\frac{\alpha_{i-1}(y_{i-1}|x)M_i(y_{i-1},y_i|x)\beta_i(y_i|x)}{Z(x)}\end{aligned}$$
第一個等號,可以看出計算代價非常大,但轉化為第二個等號後,便可利用前向向量和後向向量來高效計算。
(2)特征函數 $f_k$ 關於聯合分布 P(X,Y) 的期望:
這裏假設已知邊緣分布 P(X) 的經驗分布為 $\widetilde P(X)$ ,經驗分布就是根據訓練數據,用頻數估計的方式得到 $\widetilde P(X=x)=\dfrac{\#x}{N}$。
$$\begin{aligned}\mathbb E_{P(X,Y)}[f_k]&=\sum_{x,y}P(x,y)f_k(y,x)\\&=\sum_x\widetilde P(x)\sum_{y}P(Y=y|x)\sum_{i=1}^{n+1} f_k(y_{i-1},y_i,x,i)\\&=\sum_x\widetilde P(x)\sum_{i=1}^{n+1}\sum_{y_{i-1}y_i}f_k(y_{i-1},y_i,x,i)\frac{\alpha_{i-1}(y_{i-1}|x)M_i(y_{i-1},y_i|x)\beta_i(y_i|x)}{Z(x)}\end{aligned}$$
第二個等號那裏類似於最大熵模型的條件熵的定義。
對於給定的觀測序列 x 和標記序列 y ,通過一次前向掃描計算 $\boldsymbol\alpha_i$ 及 $Z(x)$ ,一次後向掃描計算 $\boldsymbol\beta_i$ ,進而計算所有的概率值,以及特征的期望。
三、線性鏈條件隨機場的解碼問題
解碼問題即預測問題,給定條件隨機場 P(Y|X) 和觀測序列 x ,求最有可能的狀態序列 y* 。與 HMM 類似,使用維特比算法求解。
四、線性鏈條件隨機場的學習問題
CRF是定義在時序數據上的對數線性模型,使用 MLE 和帶正則的 MLE 來訓練。類似於最大熵模型,可以用改進的叠代尺度法(IIS)和擬牛頓法(如BFGS算法)來訓練。
訓練數據 $\{(x^{(j)},y^{(j)})\}_{j=1}^N$ 的對數似然函數為
$$\begin{aligned}L(\textbf w)=L_{\widetilde P}(P_\textbf w)&=\ln\prod_{j=1}^NP_{\textbf w}(Y=y^{(j)}|x^{(j)})\\&=\sum_{j=1}^N\ln P_{\textbf w}(Y=y^{(j)}|x^{(j)})\\&=\sum_{j=1}^N\ln \frac{\exp\sum_{k=1}^Kw_kf_k(y^{(j)},x^{(j)})}{Z_{\textbf w}(x^{(j)})}\\&=\sum_{j=1}^N\biggl(\sum_{k=1}^Kw_kf_k(y^{(j)},x^{(j)})-\ln Z_{\textbf w}(x^{(j)})\biggr)\end{aligned}$$
或者可以這樣寫:
$$\begin{aligned}L(\textbf w)=L_{\widetilde P}(P_\textbf w)&=\ln\prod_{x,y}P_{\textbf w}(Y=y|x)^{\widetilde P(x,y)}\\&=\sum_{x,y}\widetilde P(x,y)\ln P_{\textbf w}(Y=y|x)\\&=\sum_{x,y}\widetilde P(x,y)\ln \frac{\exp\sum_{k=1}^Kw_kf_k(y,x)}{Z_{\textbf w}(x)}\\&=\sum_{x,y}\widetilde P(x,y)\sum_{k=1}^Kw_kf_k(y,x)-\sum_{x,y}\widetilde P(x,y)\ln Z_{\textbf w}(x)\\&=\sum_{x,y}\widetilde P(x,y)\sum_{k=1}^Kw_kf_k(y,x)-\sum_{x}\widetilde P(x)\ln Z_{\textbf w}(x)\end{aligned}$$
最後一個等號是因為 $\sum_yP(Y=y|x)=1$ 。順便求個導:
$$\begin{aligned}\frac{\partial L(\textbf w)}{\partial w_i}&=\sum_{x,y}\widetilde P(x,y)f_i(x,y)-\sum_{x,y}\widetilde P(x)P_{\textbf w}(Y=y|x)f_i(x,y)\\&=\mathbb E_{\widetilde P(X,Y)}[f_i]-\sum_{x,y}\widetilde P(x)P_{\textbf w}(Y=y|x)f_i(x,y)\end{aligned}$$
似然函數中的 $\ln Z_{\textbf w}(x)$ 項是一個指數函數的和的對數的形式。關於這一項在編程過程中需要註意的地方可以參考這篇博客。
參考:
[1] 統計學習方法
[2] Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence Data
[3] Conditional Random Fields: An Introduction
[4] An Introduction to Conditional Random Fields for Relational Learning
[5] Introduction to Conditional Random Fields
[6] 數值優化:理解L-BFGS算法
[7] 牛頓法與擬牛頓法學習筆記(五)L-BFGS 算法
[8] CRF++代碼分析
[9] 漫步條件隨機場系列文章
NLP —— 圖模型(二)條件隨機場(Conditional random field,CRF)
