“等一下,我碰!”——常見的2D碰撞檢測
轉自:https://aotu.io/notes/2017/02/16/2d-collision-detection/
在 2D 環境下,常見的碰撞檢測方法如下:
- 外接圖形判別法
- 軸對稱包圍盒(Axis-Aligned Bounding Box),即無旋轉矩形。
- 圓形碰撞
- 圓形與矩形(無旋轉)
- 圓形與旋轉矩形(以矩形中心點為旋轉軸)
- 光線投射法
- 分離軸定理
- 其他
- 地圖格子劃分
- 像素檢測
下文將由易到難的順序介紹上述各種碰撞檢測方法:外接圖形判別法 > 其他 > 光線投射法 > 分離軸定理。
另外,有一些場景只要我們約定好限定條件,也能實現我們想要的碰撞,如下面的碰壁反彈:

當球碰到邊框就反彈(如x/y軸方向速度取反)。
if(ball.left < 0 || ball.right > rect.width) ball.velocityX = -ball.velocityX if(ball.top < 0 || ball.bottom > rect.height) ball.velocityY = -ball.velocityY
再例如當一個人走到 100px 位置時不進行跳躍,就會碰到石頭等等。
因此,某些場景只需通過設定到適當的參數即可實現碰撞檢測。
外接圖形判別法
軸對稱包圍盒(Axis-Aligned Bounding Box)
概念:判斷任意兩個(無旋轉)矩形的任意一邊是否無間距,從而判斷是否碰撞。
算法:
rect1.x < rect2.x + rect2.width && rect1.x + rect1.width > rect2.x && rect1.y < rect2.y + rect2.height && rect1.height + rect1.y > rect2.y
兩矩形間碰撞的各種情況:
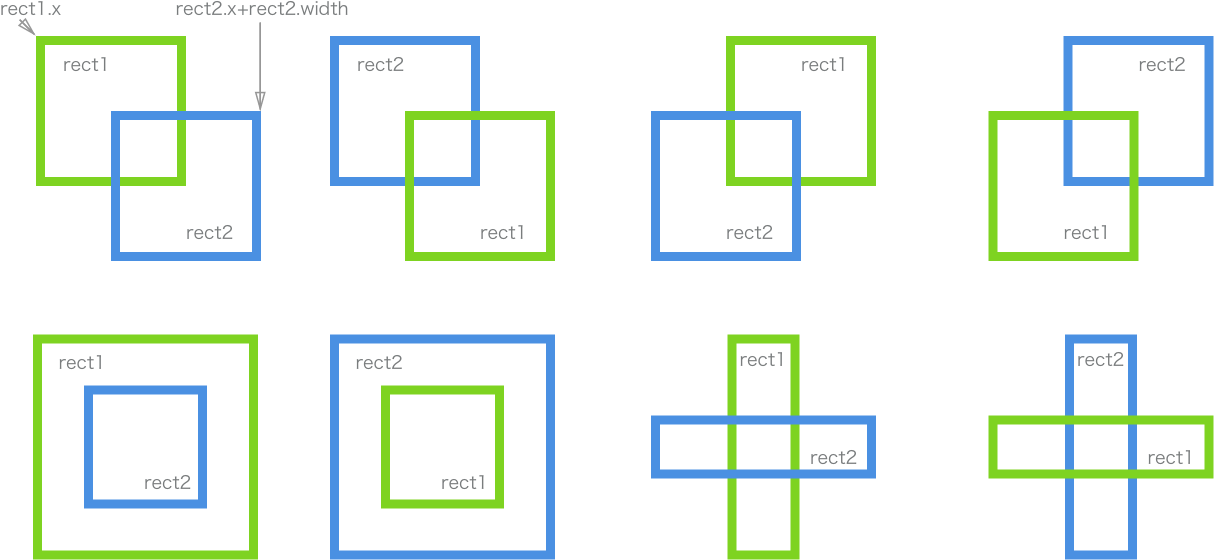
在線運行示例(先點擊運行示例以獲取焦點,下同):

缺點:
- 相對局限:兩物體必須是矩形,且均不允許旋轉(即關於水平和垂直方向上對稱)。
- 對於包含著圖案(非填滿整個矩形)的矩形進行碰撞檢測,可能存在精度不足的問題。
- 物體運動速度過快時,可能會在相鄰兩動畫幀之間快速穿越,導致忽略了本應碰撞的事件發生。
適用案例:
- (類)矩形物體間的碰撞。
圓形碰撞(Circle Collision)
概念:通過判斷任意兩個圓形的圓心距離是否小於兩圓半徑之和,若小於則為碰撞。
兩點之間的距離由以下公式可得: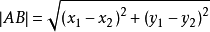
判斷兩圓心距離是否小於兩半徑之和:
Math.sqrt(Math.pow(circleA.x - circleB.x, 2) + Math.pow(circleA.y - circleB.y, 2)) < circleA.radius + circleB.radius
圖例:
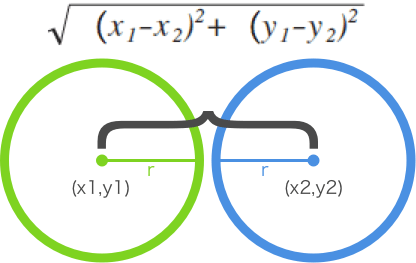
在線運行示例:

缺點:
- 與『軸對稱包圍盒』類似
適用案例:
- (類)圓形的物體,如各種球類碰撞。
圓形與矩形(無旋轉)
概念:通過找出矩形上離圓心最近的點,然後通過判斷該點與圓心的距離是否小於圓的半徑,若小於則為碰撞。
那如何找出矩形上離圓心最近的點呢?下面我們從 x 軸、y 軸兩個方向分別進行尋找。為了方便描述,我們先約定以下變量:
矩形上離圓心最近的點為變量:closestPoint = {x, y}; 矩形 rect = {x, y, w, h}; // 左上角與寬高 圓形 circle = {x, y, r}; // 圓心與半徑
首先是 x 軸:
如果圓心在矩形的左側(if(circle.x < rect.x)),那麽 closestPoint.x = rect.x。
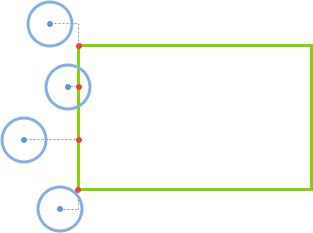
如果圓心在矩形的右側(else if(circle.x > rect.x + rect.w)),那麽 closestPoint.x = rect.x + rect.w。
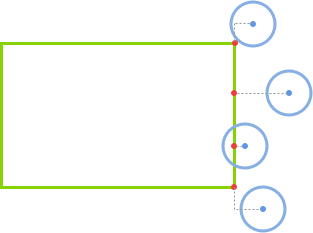
如果圓心在矩形的正上下方(else),那麽 closestPoint.x = circle.x。
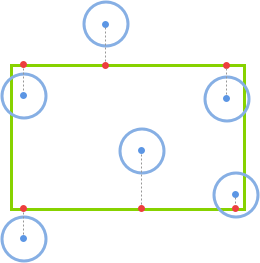
同理,對於 y 軸(此處不列舉圖例):
如果圓心在矩形的上方(if(circle.y < rect.y)),那麽 closestPoint.y = rect.y。
如果圓心在矩形的下方(else if(circle.y < rect.y + rect.h)),那麽 closestPoint.y = rect.y + rect.h。
圓形圓心在矩形的正左右兩側(else),那麽 closestPoint.y = circle.y。
因此,通過上述方法即可找出矩形上離圓心最近的點了,然後通過『兩點之間的距離公式』得出『最近點』與『圓心』的距離,最後將其與圓的半徑相比,即可判斷是否發生碰撞。
var distance = Math.sqrt(Math.pow(closestPoint.x - circle.x, 2) + Math.pow(closestPoint.y - circle.y, 2)) if(distance < circle.r) return true // 發生碰撞 else return false // 未發生碰撞
在線運行示例:
缺點:
- 矩形需是軸對稱的,即不能旋轉。
圓形與旋轉矩形(以矩形中心為旋轉軸)
概念:即使矩形以其中心為旋轉軸進行了旋轉,但是判斷它與圓形是否發生碰撞的本質還是找出矩形上離圓心的最近點。
對於旋轉後的矩形,要找出其離圓心最近的點,視乎有些困難。其實,我們可以將我們思想的範圍進行擴大:將矩形的旋轉看作是整個畫布的旋轉。那麽我們將畫布(即 Canvas)反向旋轉『矩形旋轉的角度』後,所看到的結果就是上一個方法“圓形與矩形(無旋轉)”的情形。因此,我們只需求出畫布旋轉後的圓心位置,即可使用『圓形與矩形(無旋轉)』的判斷方法了。
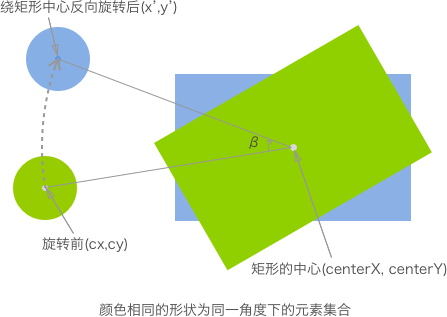
先給出可直接套用的公式,從而得出旋轉後的圓心坐標:
x’ = cos(β) * (cx – centerX) – sin(β) * (cy – centerY) + centerX
y’ = sin(β) * (cx – centerX) + cos(β) * (cy – centerY) + centerY
下面給出該公式的推導過程:
根據下圖,計算某個點繞另外一個點旋轉一定角度後的坐標。我們設 A(x,y) 繞 B(a,b) 旋轉 β 度後的位置為 C(c,d)。
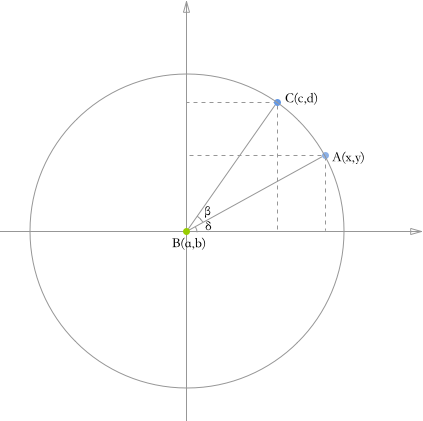
- 設 A 點旋轉前的角度為 δ,則旋轉(逆時針)到 C 點後的角度為(δ+β)
- 由於 |AB| 與 |CB| 相等(即長度),且
- |AB| = y/sin(δ) = x / cos(δ)
- |CB| = d/sin(δ + β) = c / cos(δ + β)
- 半徑 r = x / cos(δ) = y / sin(δ) = d / sin(δ + β) = c / cos(δ + β)
- 由以下三角函數兩角和差公式:
- sin(δ + β) = sin(δ)cos(β) + cos(δ)sin(β)
- cos(δ + β) = cos(δ)cos(β) - sin(δ)sin(β)
- 可得出旋轉後的坐標:
- c = r * cos(δ + β) = r * cos(δ)cos(β) - r * sin(δ)sin(β) = x * cos(β) - y * sin(β)
- d = r * sin(δ + β) = r * sin(δ)cos(β) + r * cos(δ)sin(β) = y * cos(β) + x * sin(β)
由上述公式推導後可得:旋轉後的坐標 (c,d) 只與旋轉前的坐標 (x,y) 及旋轉的角度 β 有關。
當然,(c,d) 是旋轉一定角度後『相對於旋轉點(軸)的坐標』。因此,前面提到的『可直接套用的公式』中加上了矩形的中心點的坐標值。
從圖中也可以得出以下結論:A 點旋轉後的 C 點總是在圓周(半徑為 |AB|)上運動,利用這點可讓物體繞旋轉點(軸)做圓周運動。
得到旋轉後的圓心坐標值後,即可使用『圓形與矩形(無旋轉)』方法進行碰撞檢測了。
在線運行案例:
優點:
- 相對於圓形與矩形(未旋轉)的方法,適用範圍更廣。
其他
地圖格子劃分
概念:將地圖(場景)劃分為一個個格子。地圖中參與檢測的對象都存儲著自身所在格子的坐標,那麽你即可以認為兩個物體在相鄰格子時為碰撞,又或者兩個物體在同一格才為碰撞。另外,采用此方式的前提是:地圖中所有可能參與碰撞的物體都要是格子單元的大小或者是其整數倍。
藍色X 為障礙物:

實現方法:
// 通過特定標識指定(非)可行區域 map = [ [0, 0, 1, 1, 1, 0, 0, 0, 0], [0, 1, 1, 0, 0, 1, 0, 0, 0], [0, 1, 0, 0, 0, 0, 1, 0, 0], [0, 1, 0, 0, 0, 0, 1, 0, 0], [0, 1, 1, 1, 1, 1, 1, 0, 0] ], // 設定角色的初始位置 player = {left: 2, top: 2} // 移動前(後)判斷角色的下一步的動作(如不能前行) ...
在線運行示例:

缺點:
- 適用場景局限。
適用案例:
- 推箱子、踩地雷等
像素檢測
概念:以像素級別檢測物體之間是否存在重疊,從而判斷是否碰撞。
實現方法有多種,下面列舉在 Canvas 中的兩種實現方式:
- 如下述的案例中,通過將兩個物體在 offscreen canvas 中判斷同一位置(坐標)下是否同時存在非透明的像素。
- 利用 canvas 的
globalCompositeOperation = ‘destination-in‘屬性。該屬性會讓兩者的重疊部分會被保留,其余區域都變成透明。因此,若存在非透明像素,則為碰撞。
註意,當待檢測碰撞物體為兩個時,第一種方法需要兩個 offscreen canvas,而第二種只需一個。
當然,我們這裏並不是利用 offscreen render 的性能優勢,而是利用 offscreen canvas 保存獨立物體的像素。換句話說:onscreen canvas 只是起展示作用,碰撞檢測是在 offscreen canvas 中進行。
另外,由於需要逐像素檢測,若對整個 Canvas 內所有像素都進行此操作,無疑會浪費很多資源。因此,我們可以先通過運算得到兩者相交區域,然後只對該區域內的像素進行檢測即可。
圖例:
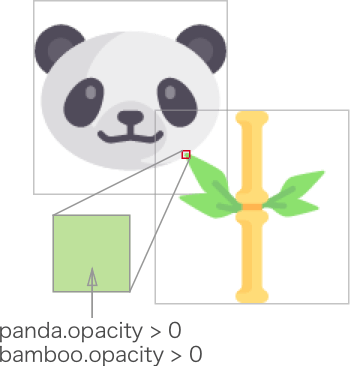
下面示例展示了第一種實現方式:
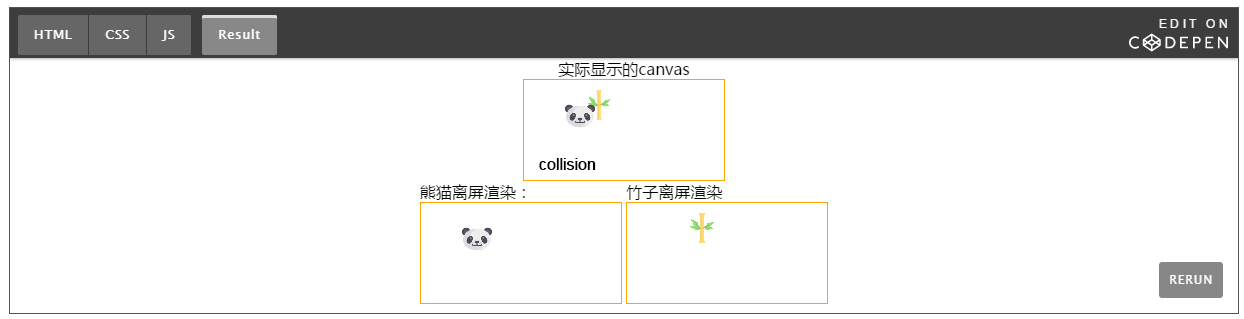
缺點:
- 因為需要檢查每一像素來判定是否碰撞,性能要求比較高。
適用案例:
- 需要以像素級別檢測物體是否碰撞。
光線投射法(Ray Casting)
概念:通過檢測兩個物體的速度矢量是否存在交點,且該交點滿足一定條件。
對於下述拋小球入桶的案例:畫一條與物體的速度向量相重合的線(#1),然後再從另一個待檢測物體出發,連線到前一個物體,繪制第二條線(#2),根據兩條線的交點位置來判定是否發生碰撞。
拋球進桶圖例:
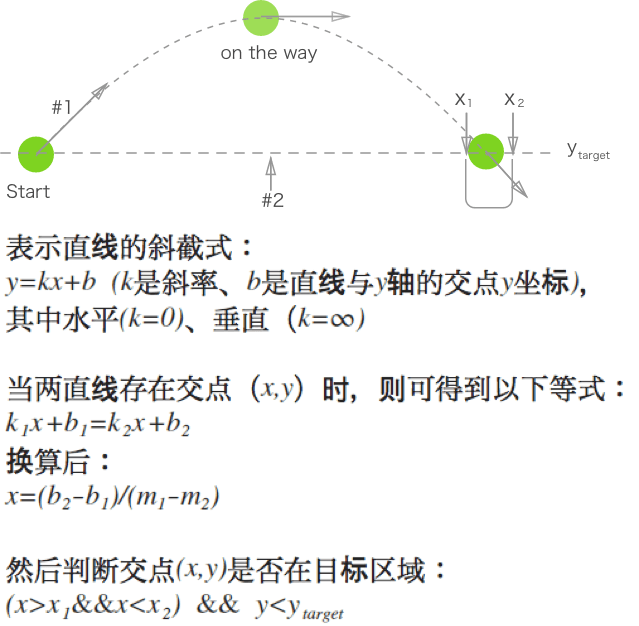
在小球飛行的過程中,需要不斷計算兩直線的交點。
當滿足以下兩個條件時,那麽應用程序就可以判定小球已落入桶中:
- 兩直線交點在桶口的左右邊沿間
- 小球位於第二條線(
#2)下方
在線運行示例:
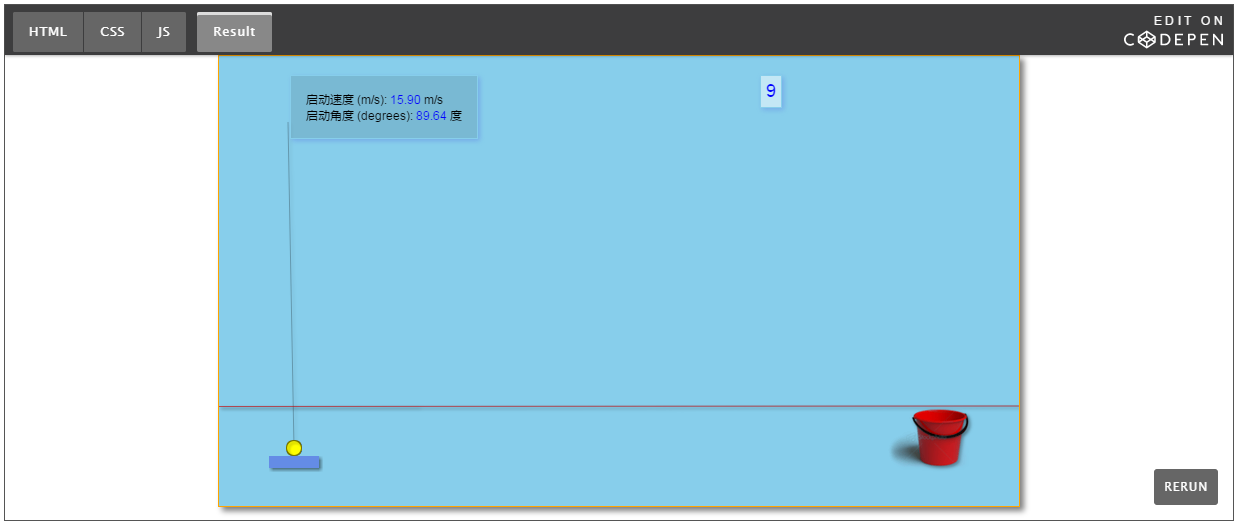
優點:
- 適合運動速度快的物體
缺點:
- 適用範圍相對局限。
適用案例:
- 拋球運動進桶。
分離軸定理(Separating Axis Theorem)
概念:通過判斷任意兩個 凸多邊形 在任意角度下的投影是否均存在重疊,來判斷是否發生碰撞。若在某一角度光源下,兩物體的投影存在間隙,則為不碰撞,否則為發生碰撞。
圖例:
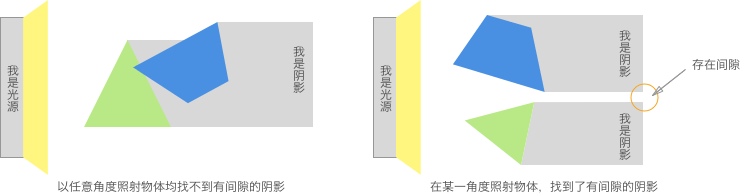
在程序中,遍歷所有角度是不現實的。那如何確定 投影軸 呢?其實投影軸的數量與多邊形的邊數相等即可。

以較高抽象層次判斷兩個凸多邊形是否碰撞:
function polygonsCollide(polygon1, polygon2) { var axes, projection1, projection2 // 根據多邊形獲取所有投影軸 axes = polygon1.getAxes() axes.push(polygon2.getAxes()) // 遍歷所有投影軸,獲取多邊形在每條投影軸上的投影 for(each axis in axes) { projection1 = polygon1.project(axis) projection2 = polygon2.project(axis) // 判斷投影軸上的投影是否存在重疊,若檢測到存在間隙則立刻退出判斷,消除不必要的運算。 if(!projection1.overlaps(projection2)) return false } return true }
上述代碼有幾個需要解決的地方:
- 如何確定多邊形的各個投影軸
- 如何將多邊形投射到某條投影軸上
- 如何檢測兩段投影是否發生重疊
投影軸
如下圖所示,我們使用一條從 p1 指向 p2 的向量來表示多邊形的某條邊,我們稱之為邊緣向量。在分離軸定理中,還需要確定一條垂直於邊緣向量的法向量,我們稱之為“邊緣法向量”。
投影軸平行於邊緣法向量。投影軸的位置不限,因為其長度是無限的,故而多邊形在該軸上的投影是一樣的。該軸的方向才是關鍵的。
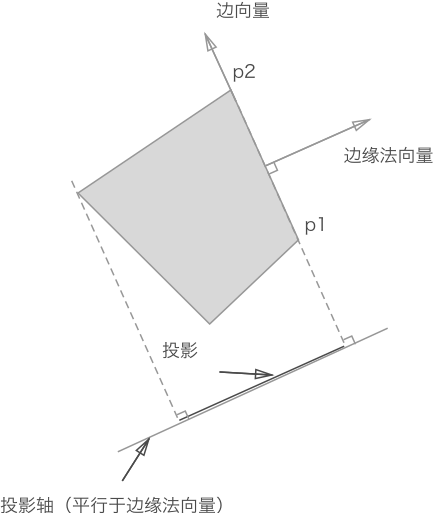
// 以原點(0,0)為始,頂點為末。最後通過向量減法得到 邊緣向量。 var v1 = new Vector(p1.x, p1.y) v2 = new Vector(p2.x, p2.y) // 首先得到邊緣向量,然後再通過邊緣向量獲得相應邊緣法向量(單位向量)。 // 兩向量相減得到邊緣向量 p2p1(註:上面應該有個右箭頭,以表示向量)。 // 設向量 p2p1 為(A,B),那麽其法向量通過 x1x2+y1y2 = 0 可得:(-B,A) 或 (B,-A)。 axis = v1.edge(v2).normal()
以下是向量對象的部分實現,具體可看源碼。
var Vector = function(x, y) { this.x = x this.y = y } Vector.prototype = { // 獲取向量大小(即向量的模),即兩點間距離 getMagnitude: function() { return Math.sqrt(Math.pow(this.x, 2), Math.pow(this.y, 2)) }, // 點積的幾何意義之一是:一個向量在平行於另一個向量方向上的投影的數值乘積。 // 後續將會用其計算出投影的長度 dotProduct: function(vector) { return this.x * vector.x + this.y + vector.y }, // 向量相減 得到邊 subtarct: function(vector) { var v = new Vector() v.x = this.x - vector.x v.y = this.y - vector.y return v }, edge: function(vector) { return this.substract(vector) }, // 獲取當前向量的法向量(垂直) perpendicular: function() { var v = new Vector() v.x = this.y v.y = 0 - this.x return v }, // 獲取單位向量(即向量大小為1,用於表示向量方向),一個非零向量除以它的模即可得到單位向量 normalize: function() { var v = new Vector(0, 0) m = this.getMagnitude() if(m !== 0) { v.x = this.x / m v.y = this.y /m } return v }, // 獲取邊緣法向量的單位向量,即投影軸 normal: function() { var p = this.perpendicular() return p .normalize() } }
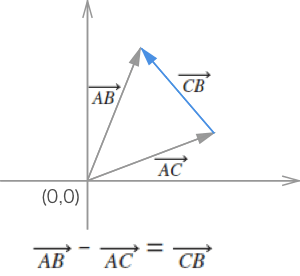
向量相減
更多關於向量的知識可通過其它渠道學習。
投影
投影的大小:通過將一個多邊形上的每個頂點與原點(0,0)組成的向量,投影在某一投影軸上,然後保留該多邊形在該投影軸上所有投影中的最大值和最小值,這樣即可表示一個多邊形在某投影軸上的投影了。
判斷兩多邊形的投影是否重合:projection1.max > projection2.min && project2.max > projection.min
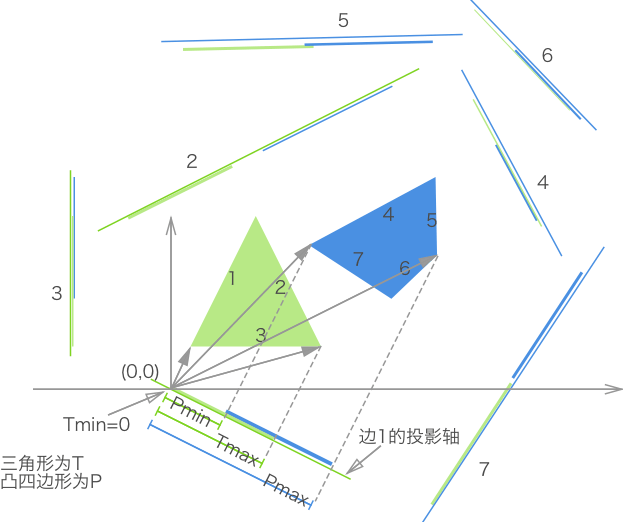
為了易於理解,示例圖將坐標軸原點(0,0)放置於三角形邊1投影軸的適當位置。
由上述可得投影對象:
// 用最大和最小值表示某一凸多邊形在某一投影軸上的投影位置 var Projection = function (min, max) { this.min this.max } projection.prototype = { // 判斷兩投影是否重疊 overlaps: function(projection) { return this.max > projection.min && projection.max > this.min } }
如何得到向量在投影軸上的長度?
向量的點積的其中一個幾何含義是:一個向量在平行於另一個向量方向上的投影的數值乘積。
由於投影軸是單位向量(長度為1),投影的長度為 x1 * x2 + y1 * y2
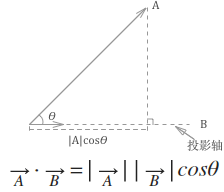
// 根據多邊形的每個定點,得到投影的最大和最小值,以表示投影。 function project = function (axis) { var scalars = [], v = new Vector() this.points.forEach(function (point) { v.x = point.x v.y = point.y scalars.push(v.dotProduct(axis)) }) return new Projection(Math.min.apply(Math, scalars), Math.max,apply(Math, scalars)) }
圓形與多邊形之間的碰撞檢測
由於圓形可近似地看成一個有無數條邊的正多邊形,而我們不可能按照這些邊一一進行投影與測試。我們只需將圓形投射到一條投影軸上即可,這條軸就是圓心與多邊形頂點中最近的一點的連線,如圖所示:
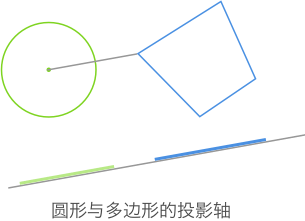
因此,該投影軸和多邊形自身的投影軸就組成了一組待檢測的投影軸了。
而對於圓形與圓形之間的碰撞檢測依然是最初的兩圓心距離是否小於兩半徑之和。
分離軸定理的整體代碼實現,可查看以下案例:
優點:
- 精確
缺點:
- 不適用於凹多邊形
適用案例:
- 任意凸多邊形和圓形。
更多關於分離軸定理的資料:
- Separating Axis Theorem (SAT) explanation
- Collision detection and response
- Collision detection Using the Separating Axis Theorem
- SAT (Separating Axis Theorem)
- Separation of Axis Theorem (SAT) for Collision Detection
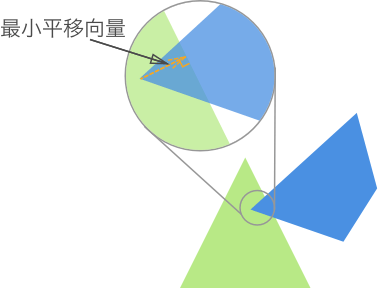
延伸:最小平移向量(MIT)
通常來說,如果碰撞之後,相撞的雙方依然存在,那麽就需要將兩者分開。分開之後,可以使原來相撞的兩物體彼此彈開,也可以讓他們黏在一起,還可以根據具體需要來實現其他行為。不過首先要做的是,還是將兩者分開,這就需要用到最小平移向量(Minimum Translation Vector, MIT)。
碰撞性能優化
若每個周期都需要對全部物體進行兩兩判斷,會造成浪費(因為有些物體分布在不同區域,根本不會發生碰撞)。所以,大部分遊戲都會將碰撞分為兩個階段:粗略和精細(broad/narrow)。
粗略階段(Broad Phase)
Broad phase 能為你提供有可能碰撞的實體列表。這可通過一些特殊的數據結構實現,它們能為你提供信息:實體存在哪裏和哪些實體在其周圍。這些數據結構可以是:四叉樹(Quad Trees)、R樹(R-Trees)或空間哈希映射(Spatial Hashmap)等。
讀者若感興趣,可以自行查閱相關信息。
精細階段(Narrow Phase)
當你有了較小的實體列表,你可以利用精細階段的算法(如上述講述的碰撞算法)得到一個確切的答案(是否發生碰撞)。
最後
碰撞檢測有多種,選擇合適最重要。
完!
參考資料
- MDN:2D collision detection
- 《HTML5 Canvas 核心技術:圖形、動畫與遊戲開發》
- Circular Collision Detection
- Circle and Rotated Rectangle Collision Detection
- 推導坐標旋轉公式
“等一下,我碰!”——常見的2D碰撞檢測
