[算法 樹狀數組]
要學樹狀數組的先看懂一幅圖
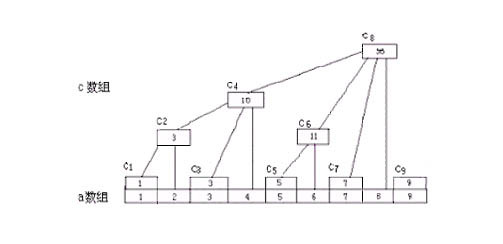
這就是樹狀數組的存儲方式。
那麽樹狀數組的優點是什麽呢,允許任意修改,可快速提取出a數組內數字
據圖可知
c1=a1,
c2=a1+a2,
c3=a3,
c4=a1+a2+a3+a4,
c5=a5,
c6=a5+a6,
c7=a7,
c8=a1+a2+a3+a4+a5+a6+a7+a8,
c9=a9,
c10=a9+a10,
c11=a11.......
.c16=a1+a2+a3+a4+a5+.......+a16。
分析上面的幾組式子可知,當 i 為奇數時,ci=ai ;當 i 為偶數時,就要看 i 的因子中最多有二的多少次冪,例如,6 的因子中有 2 的一次冪,等於 2 ,所以 c6=a5+a6(由六向前數兩個數的和),4 的因子中有 2 的兩次冪,等於 4 ,所以 c4=a1+a2+a3+a4(由四向前數四個數的和)。
(一)因此得到公式 cn=a(n-a^k+1)+.........+an(其中 k 為 n 的二進制表示中從右往左數的 0 的個數)。
那麽,如何求 a^k 呢?求法如下:
1 int lowbit(int x)
2 {
3 return x&(-x);
4 }
為啥那?
以68為例,他的二進制是(68)2=1000100. 那麽-68呢?因為計算機裏的整數采用補碼表示(補碼是原碼取反加一),因此-68實際上是68按位取反,末尾加一以後的結果。如下表(忽略符號位):
原碼 1 0 0 0 1 0 0
↓
反碼 0 1 1 1 0 1 1
↓
補碼 0 1 1 1 1 0 0
我們把(68)2和(-68)2放在一起看一看:
1 0 0 0 1 0 0
0 1 1 1 1 0 0
發現他們末尾帶的0是一樣多的。因此lowbit(x)=x&-x. (&是轉換成二進制之後進行與運算;而&&是直接進行與運算)
(二)由此,我們就可以求出c數組了
1 int sum(int x) 2 { 3 int sum=0; 4 while(x>0) 5 { 6 sum+=c[x]; 7 x-=lowbit(x); 8 } 9 }
(三)當數組中的元素有變更時,樹狀數組就發揮它的優勢了,算法如下(修改為給某個節點 i 加上 x ):
1 void change(int i,int x) 2 { 3 while(i<=n) 4 { 5 c[i]+=x; 6 i+=lowbit(i) 7 } 8 }
嗯。就這樣。不算難。大概就是一種可變更的存儲方式吧
[算法 樹狀數組]
