不相交集類
轉載請註明出處：https://i.cnblogs.com/EditPosts.aspx?postid=5748920
一、基本概念
不相交集類維持著多個彼此之間沒有交集的子集的集合，可以用於 判斷兩個元素是否屬於同一個集合，或者合並兩個不相交的子集。比如，
{ {1,3,5}，{2}，{4}，{6,7} }
這整體就是一個不相交集合。裏面的一些子集也是彼此互不相交的。
註意，對於每一個子集，往往用某一個元素來代表，至於用哪一個元素來表示則沒有硬性要求。只要能夠保證對於某一個子集中的元素查找兩次它的代表，返回的值是相同的即可。還是上面的例子，
假設 1作為第一個子集的代表，find(1)、find(3)、find(5)都應該返回 1。而如果find(1)返回的是 1，find(3)返回的是 3，我們就可能認為兩個元素不在同一個集合裏，而事實並不是這樣。
對於不相交集類，我們重點關註以下三個操作：
1.makeSet(x)，建立一個新的只含有元素 x的集合。
2.union(x,y)，將 x、y所在的子集（Sx和 Sy）合並成一個新的子集，並為了保證新集合的子集不相交性，消除原來集合中的 Sx和 Sy。
3.find(x)，返回元素 x所在的集合的代表。
二、不相交集類的鏈表表示
使用鏈表來表示不相交集類是比較簡單的。對於鏈表中的每一個對象，包含一個數據成員，指向所在集合的代表的指針和指向下一個節點的指針，如圖 1所示。
每一個子集用一個鏈表表示，鏈表中的第一個節點代表了當前子集。另外，對於每一個鏈表，還設置了 head指針和 tail指針。其中， head指針指向當前子集的代表，tail指針則指向當前子集的最後一個元素，如圖 2所示。
下面來分析使用這樣的數據結構，其操作是如何完成的和其時間復雜度如何。
1.makeSet(x)，只需要建立一個只含有元素值x的節點的鏈表，時間復雜度為 O(1)。
2.find(x)，只需要返回其所指向的代表指針所指向的節點的數據成員即可，時間復雜度為 O(1)。
3.union(x,y)，根據合並時所采用的策略，可以分為兩種
3.1 將 x所在的鏈表合並到 y所在的鏈表中
此時，合並後的鏈表是以 y鏈表的第一個節點作為當前集合的代表的，這樣就需要將原來 x鏈表的指向代表的指針都修改為指向 y鏈表的第一個節點，修改次數與 x鏈表的長度一致。如圖 3所示。
假設含有 n個不相交子集的集合 S，初始狀態下每個集合都只含有一個元素 xi。
第一次，執行 union(x1,x2)，需要 1次操作；
第二次，執行 union(x2,x3)，需要 2次操作；
......
第 i次，執行 union(xi,xi+1)，需要 i次操作；
......
第 n-1次，執行 union(xn-1,xn)，需要 n-1次操作；
由於總的元素子集個數只有 n個，所以 union的最大次數為 n-1。這樣，對於連續 n-1次 union，總的操作次數為 1+2+...+n-1 = O(n2)。平均來看，每一次 union操作的攤還時間為 O(n)。
3.2 加權合並啟發式策略——將較短的表拼到較長的表上去
仔細分析上文所述的對於含有 n個不相交子集的集合 S的合並過程，可以發現在執行 union(xi,xi+1)時，將 xi鏈合並到 xi+1鏈中，需要 i次操作，而將 xi+1鏈合並到 xi鏈中，則只需要 1次操作。那麽對於連續 n-1次從 x1到 xn的union，總的操作次數只有 n-1。
這也許是合並 n個不相交子集的集合 S的最好情形，而最壞情形就是 3.1中所描述的做法。
然而實際合並時，並不總是會有包含 x1的子集，還會有其他多種情況，比如將 {x2,x3}和{x4,x5,x6}合並到一起。但是這給了我們一個啟發，就是在合並時，將較短的表拼到較長的表上去，以此來減少修改指向代表的指針的次數。
對於某一個元素 x，一開始它是一個獨立的子集，其代表指針指向子集。
當第一次修改它的代表指針，使它指向別的元素時，說明 {x}與其它子集合並了，此時新集合的元素個數至少是 2；
當第二次修改它的代表指針，說明與其合並的子集的元素個數至少為 2，那麽此時新集合的元素個數至少是 4；
......
當第 k次修改它的代表指針，說明與其合並的子集的元素個數至少為 2k-1，那麽此時新集合的元素個數至少是 2k；
由於總的元素子集個數只有 n個，所以最多修改 lgn次元素 x的代表指針。所以將 n個元素 union到一起，最壞情形下總共需要 nlgn次操作。即，其時間復雜度為 O(nlgn)。而最好情形則是本節一開始所說的 O(n)。
不過，對於鏈表表示，有一個很大的問題。就是以上的分析都是直接基於節點的，而不是基於節點的數據成員。比如，對於圖 2中的 find(5)，理論分析只需要返回它的代表指針即可；可是一開始並不能知道 5節點在哪裏，還是需要先遍歷當前鏈表，找到數據成員為 5的節點。
這樣一來，時間復雜度將會增加很多，實現起來也變得麻煩了。所以這裏我並沒有給出鏈表實現的代碼。（PS:這是我自己的疑問，希望各位高手能幫我解答這個疑惑，謝謝
）
三、不相交集類的根樹表示
使用一棵樹來表示一個子集，樹的根節點可以代表當前子集，而所有子集的集合就是一個森林。而對於根樹的存儲結構，采用數組實現。s[i]表示元素 i的父節點。根節點令 s[i]=-1。
註意，下面這個例子以及後面的圖會與測試中采用的數據和方法相一致，可以用來檢測所編寫程序的正確性！
圖 4 含有 10個單元素子集的根樹表示和存儲結構
同樣地，現在來考慮操作是如何完成的和其時間復雜度如何。
1.makeSet(x)，令 x成為只含有根節點的樹，並且令 s[x] = -1。
2.union(x,y)，用根樹表示的不相交子集在合並時時很容易且快速的。這裏，假設 x和 y都是根節點（不是的話，可以通過find()返回其所在樹的根節點）。簡單的做法是將 y的父鏈連接到 x節點上，比如 union(6,7)，圖 4變成了下面圖 5所示的情形.
圖 5 union(6,7)
接著，union(4,5)，有
圖 6 union(4,5)
然後，再 union(4,6)，有
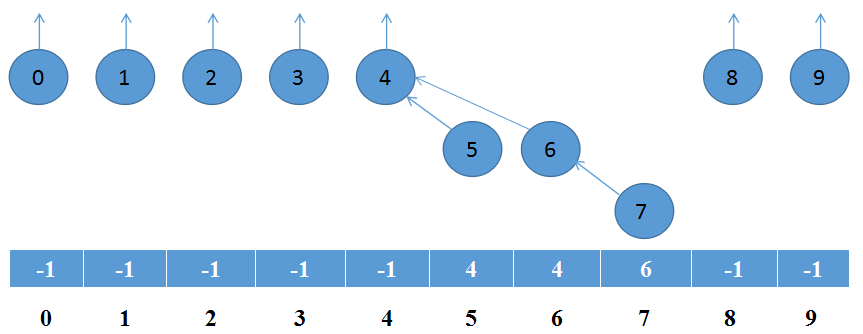
圖 7 union(4,6)
可以看到，前面的合並方法是相當隨意的，它通過使第二顆樹成為第一顆樹的子樹而完成合並。這樣做有一個隱患，那就是這可能會導致某些樹的深度增加過大，從而增加 find()操作的時間復雜度。
這裏，采用兩種靈巧求並算法來完成合並操作。
2.1 按大小求並
合並的時候先檢查樹的大小，使較小的樹成為較大的數的子樹。這樣的話，需要在根節點處記錄每一顆樹的大小。由於已經令根節點的 s[i]=-1了，這裏，可以直接用根節點的 s[i]存儲樹的大小。而當按大小合並時，將較小樹的大小加到較大樹上去，並且令較小樹的父鏈指向較大樹的根節點。
下圖比較了再執行 union(3,4)時隨意合並與按大小求並的結果有何不同。
和
圖 8 使第二顆樹成為第一顆樹的子樹而完成合並 圖 9 按大小求並
2.2 按高度（秩）求並
按高度求並可以看做是按大小求並的簡單修改，因為對於根樹結構，節點個數多並不意味著高度就越大。對於以下兩棵樹而言，使用按高度求並得到的結果深度更小。
和
；按大小求並，有
；按高度求並，有
圖 10 按大小合並與按高度合並的區別
同樣地，在合並兩顆樹時，將高度較小的樹合並到高度較大的樹中。只有在兩顆子樹的高度相同時，新樹的高度才會增加 1。同樣地，此時根節點的 s[i]存儲的是樹的高度。當樹中只有一個根節點時，s[i]=-1；而當樹的高度增 1的時候，使用 --操作符，因為此時采用的是樹的高度的相反數。
使用按高度求並，執行 union(3,4)，有
圖 11 union(4,6)
3.find(x)，尋找節點 x所在的樹的根節點。一般來說，不停地通過父鏈向上尋找，就可以找到 x所在的樹的根節點。這裏，可以進行一些改進，在執行 find(x)的過程中同時實現路徑壓縮。即從 x到根節點的路徑上的每一個節點都使它的父節點變成根。
如對上圖執行完 find(7)後，有
圖 12 執行完 find(7)後的不相交集和
可以看到，此時樹的高度有所下降。另外，對於數組中 s[4]=-3，這裏采用的是上圖中的按高度求並。你也許可能會有疑問說，此時節點 4的高度為 2，為什麽 s[4]=-3？接下來就來回答這個問題。
在隨意執行 union操作時，單單使用路徑壓縮，連續 M次操作最多需要 O(MlgN)的時間。
路徑壓縮與按大小求並是完全兼容的，這就使得兩個例程可以同時實現。時間復雜度如何？
而按高度求並不完全與路徑壓縮兼容，因為路徑壓縮會改變樹的高度，而計算新的高度並不容易。怎麽辦呢？做法就是不計算，仍舊存儲沒有實行路徑壓縮之前的高度。註意，這個高度並不是樹的真實高度，而是一個估計高度，稱為秩。
按秩求並和路徑壓縮單獨實行也能改善運行時間，但一起使用可以大幅度改善運行時間。最壞運行時間為 O(mα(n))，其中α(n)是一個增長極其緩慢的函數，在大多數不相交集的應用中，都會有 α(n)≤4。因此這個運行時間接近於 O(m)。
四、不相交集類的根樹實現
完整的 C++代碼及測試代碼如下，這裏的 unionSets操作分別采用了任意合並、按大小求並和按高度求並三種方式，而 find操作則使用了簡單查找（沒有任何額外操作）和路徑壓縮兩種方式。
1 /* 2 * DisjSets.h文件，DisjSets類的聲明部分 3 * 1.註意，這裏實現的不相交集類是采用根樹表示、數組存儲的，這就帶來一個問題，對於一個節點值為 x的根節點， 4 * 有 s[x]=-1。可如果數據只有 1,2,100這 3個數，卻需要建立一個長度為 101的數組，是不是有些浪費了呢？ 5 * 2.unionSets操作分別采用了任意合並、按大小求並和按高度求並三種方式，而 find操作則使用了簡單查找（沒有任何額外操作）和路徑壓縮兩種方式。 6 * @author 塔奇克馬 @data 2016.08.08 7 */ 8 9 #pragma once 10 #include <vector> 11 using namespace std; 12 13 class DisjSets 14 { 15 public: 16 explicit DisjSets(int maxNum); 17 ~DisjSets(); 18 19 // 簡單查找，沒有像路徑壓縮之類的額外操作 20 int find(int x) const; 21 // 使用了路徑壓縮的查找操作 22 int findWithPassCompression(int x); 23 // 一般形式的查找操作，flag為 false，使用簡單查找；反之則使用了路徑壓縮 24 int find(int x, bool flag); 25 // 任意合並，將 y樹作為 x的子樹完成合並 26 void unionSets(int x, int y, bool flag = true); 27 // 按大小求並 28 void unionSetsBySize(int x, int y, bool flag = true); 29 // 按高度求並 30 void unionSetsByHeight(int x, int y, bool flag = true); 31 // 按類打印出整個不相交集合 32 void print() const; 33 private: 34 // 打印出根節點為 x的整個樹 35 void print(int x) const; 36 vector<int> s; // 存儲整個不相交集 37 };DisjSets.h文件
1 // DisjSets.cpp文件，DisjSets類的實現部分 2 3 #include "iostream" 4 #include "DisjSets.h" 5 using namespace std; 6 7 DisjSets::DisjSets(int maxNum):s(maxNum) 8 { 9 for (int i=0; i<maxNum; i++) 10 { 11 s[i] = -1; 12 } 13 } 14 15 DisjSets::~DisjSets() 16 { 17 18 } 19 20 21 // 簡單查找，沒有像路徑壓縮之類的額外操作 22 int DisjSets::find(int x) const 23 { 24 if (s[x] < 0) 25 return x; 26 else 27 return find( s[x] ); 28 } 29 30 // 使用了路徑壓縮的查找操作 31 int DisjSets::findWithPassCompression(int x) 32 { 33 if (s[x] < 0) 34 return x; 35 else 36 return s[x] = find( s[x] ); 37 } 38 39 // 一般形式的查找操作，flag為 false，使用簡單查找；反之則使用了路徑壓縮 40 int DisjSets::find(int x, bool flag) 41 { 42 if (!flag) 43 return find(x); 44 else 45 return findWithPassCompression(x); 46 } 47 48 // 任意合並，將 y樹作為 x的子樹完成合並 49 void DisjSets::unionSets(int x, int y, bool flag) 50 { 51 x = find(x,flag); y = find(y,flag); 52 s[y] = x; 53 } 54 55 // 按大小求並 56 void DisjSets::unionSetsBySize(int x, int y, bool flag) 57 { 58 x = find(x,flag); y = find(y,flag); 59 if ( s[x] <= s[y] ) // x樹更大，令 y樹成為 x的子樹 60 { 61 s[x] += s[y]; 62 s[y] = x; 63 } 64 else 65 { 66 s[y] += s[x]; 67 s[x] = y; 68 } 69 } 70 71 // 按高度求並 72 void DisjSets::unionSetsByHeight(int x, int y, bool flag) 73 { 74 x = find(x,flag); y = find(y,flag); 75 if ( s[x] > s[y] ) // y樹更深，令 x樹成為 y的子樹 76 s[x] = y; 77 else 78 { 79 if ( s[x] == s[y] ) 80 s[x]--; 81 s[y] = x; 82 } 83 } 84 85 // 按類打印出整個不相交集合 86 void DisjSets::print() const 87 { 88 cout<<"整個不相交集的全部元素為： "<<endl; 89 for (unsigned int i=0; i<s.size(); i++) 90 cout<<i<<" "; 91 cout<<endl; 92 int numOfChildSets = 0; 93 for (unsigned int i=0; i<s.size(); i++) 94 { 95 if ( s[i] < 0 ) 96 { 97 cout<<"第 "<<++numOfChildSets<<"個子集： "; 98 print( i ); 99 cout<<endl; 100 } 101 } 102 cout<<"總共有 "<<numOfChildSets<<"個子集"<<endl; 103 cout<<"s中的元素值："<<endl; 104 for (unsigned int i=0; i<s.size(); i++) 105 cout<<s[i]<<" "; 106 cout<<endl; 107 } 108 109 // 打印出根節點為 x的整個樹 110 void DisjSets::print(int x) const 111 { 112 cout<<x<<" "; 113 for (unsigned int j=0; j<s.size(); j++) 114 { 115 if ( x == s[j] ) 116 print(j); 117 } 118 }DisjSets.cpp文件
1 #include "iostream" 2 #include "DisjSets.h" 3 using namespace std; 4 5 void main() 6 { 7 DisjSets disjSets(10); 8 disjSets.print(); 9 10 ////////////隨意合並////////////////// 11 disjSets.unionSets(6, 7, false); 12 disjSets.unionSets(4, 5, false); 13 disjSets.unionSets(4, 6, false); 14 disjSets.unionSets(3, 4, false); 15 disjSets.print(); 16 17 //////////////按大小合並////////////////// 18 disjSets.unionSetsBySize(6, 7, false); 19 disjSets.unionSetsBySize(4, 5, false); 20 disjSets.unionSetsBySize(4, 6, false); 21 disjSets.unionSetsBySize(3, 4, false); 22 disjSets.print(); 23 24 ////////////按高度合並////////////////// 25 disjSets.unionSetsByHeight(6, 7, false); 26 disjSets.unionSetsByHeight(4, 5, false); 27 disjSets.unionSetsByHeight(4, 6, false); 28 disjSets.unionSetsByHeight(3, 4, false); 29 disjSets.print(); 30 31 disjSets.findWithPassCompression(7); 32 disjSets.print(); 33 34 system("pause"); 35 }Test_DisjSets.cpp文件
下面是測試代碼的輸出結果：
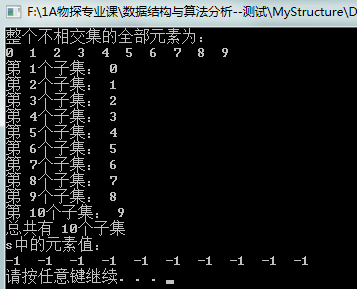與圖 4結果一致 
與圖 8結果一致 
與圖 9結果一致 
與圖 11結果一致 
與圖 12結果一致
總的來說，不相交集類是一種很有意思的數據結構。它實現起來簡單、快速，但其時間復雜度的分析卻相當困難。我看到《算法導論》和《數據結構與算法分析C++描述》中關於它的分析都很復雜，並且有些地方的結論也不太相同。所以，這裏我也不敢亂言。
對了，不相交集類可以用來生成迷宮，確定無向圖中連通子圖的個數等。
五、利用不相交集生成迷宮
不相交集類