傳送門

Description

上回說到，小Hi和小Ho接受到了河蟹先生偉大而光榮的任務：河蟹先生將要給與他們一篇從互聯網上收集來的文章，和一本厚厚的河蟹詞典，而他們要做的是判斷這篇文章中是否存在那些屬於河蟹詞典中的詞語。

當時，小Hi和小Ho的水平還是十分有限，他們只能夠想到：“枚舉每一個單詞，然後枚舉文章中可能的起始位置，然後進行匹配，看能否成功。”這樣非常樸素的想法，但是這樣的算法時間復雜度是相當高的，如果說詞典的詞語數量為N，每個詞語長度為L，文章的長度為M，那麽需要進行的計算次數是在N*M*L這個級別的，而這個數據在河蟹先生看來是不能夠接受的。

於是河蟹先生決定先給他們個機會學習一下，於是給出了一個條件N=1，也就是說詞典裏面事實上只有一個詞語，但是希望他們能夠統計這個詞語在文章中出現的次數，這便是我們常說的模式匹配問題。而小Hi和小Ho呢，通過這一周的努力，學習鉆研了KMP算法，並在互相幫助之下，已經成功的解決掉了這個問題！

這便是Hiho一下第三周發生的事情，而現在第四周到了，小Hi和小Ho也要踏上解決真正難題的旅程了呢！

小Hi和小Ho是一對好朋友，出生在信息化社會的他們對編程產生了莫大的興趣，他們約定好互相幫助，在編程的學習道路上一同前進。

這一天，他們……咳咳，說遠了，且說小Ho好不容易寫完了第三周程序，卻發現自己錯過了HihoCoder上的提交日期，於是找小Hi哭訴，小Hi雖然身為管理員，但是也不好破這個例，於是把小Ho趕去題庫交了代碼，總算是哄好了小Ho。

小Ho交完程序然後屁顛屁顛的跑回了小Hi這邊，問道：“小Hi，你說我們是不是可以去完成河蟹大大的任務了呢？”

小Hi思索半天，道：“老夫夜觀星象……啊不，我這兩天查閱了很多資料，發現這個問題其實也是很經典的問題，早在06年就有信息學奧林匹克競賽國家集訓隊的論文中詳詳細細的分析了這一問題，而他們使用的就是Trie圖這樣一種數據結構！”

“Trie圖？是不是和我們在第二周遇到的那個Trie樹有些相似呀？”小Ho問道。

“沒錯！Trie圖就是在Trie樹的基礎上發展成的一種數據結構。如果要想用一本詞典構成Trie圖的話，那麽就首先要用這本詞典構成一棵Trie樹，然後在Trie樹的基礎上添加一些邊，就能夠變成Trie圖了！”小Hi又作老師狀。

“哦！但是你說了這麽多，我都不知道Trie圖是什麽樣的呢！”小Ho無奈道。

“也是！那我們還是從頭開始，先講講怎麽用Trie樹來解決這個問題，然後在Trie樹的基礎上，討論下一步應該如何。”小Hi想了想說道。

提示一：如何用Trie樹進行“河蟹”

“現在我們有了一個時間復雜度在O(ML)級別的方法，但是我們的征途在星辰大海，啊不，我們不能滿足於這樣一個60分的方法。所以呢，我們還是要貫徹我們一貫的做法，尋找在這個算法中那些冗余的計算！“小Hi道：”那麽我們現在來看看Trie樹進行計算的時候都發生了些什麽。”

提示二：Trie樹的優化思路——後綴結點

“那麽現在……”小Hi剛要開口，就被小Ho無情打斷。

“可是小Hi老師~你看在這種情況下，結點C找不到對應的後綴結點，它對應的路徑是aaabc，而aabc在Trie裏面是走不出來的！”小Ho手中揮舞著一張紙，問道。

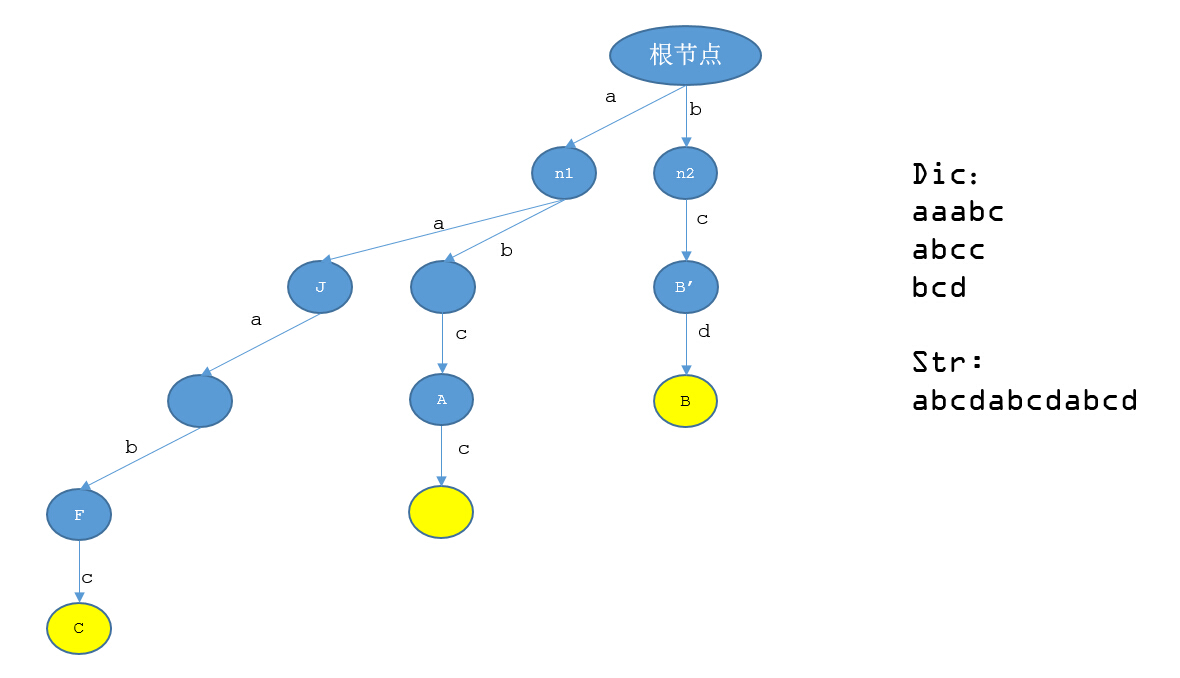
“你個瓜娃子，老是拆老子臺做啥子！……阿不，小Ho你別擔心，我這就要講解如何求後綴結點呢~”小Hi笑容滿面的說道。

提示三：如何求解Trie樹中每個結點的後綴結點

“原來如此！這樣我就知道了每一個結點的後綴結點了，接下來我就可以很輕松的解決河蟹先生交給我的問題了呢！”小Ho高興的說道：“但是，說好的Trie圖在哪裏呢？”

小Hi不由笑道：“你這叫買櫝還珠你知道麽？還記得我們再計算後綴結點的時候計算出的從每個點出發，經由每一個char（比如‘a‘..‘d‘）會走到的結點麽？把這些邊添加到Trie樹上，就是Trie圖了！”

“原來是這樣，但是這些邊感覺除了計算後綴結點之外，沒有什麽用處呀？”小Ho又開始問問題了。

“這就是Trie圖的巧妙之處了，你想想你什麽時候需要知道一個結點的後綴結點？”小Hi實在不忍看自己的兄弟這般呆萌，只能耐著性子解釋。

小Ho頓時恍然大悟，“在這個結點不能夠繼續和文章str繼續匹配了的時候，也就是這個結點沒有“文章的下一個字符”對應的那條邊，哦！我知道了，在Trie圖中，每個結點都補全了所有的邊，所以原來需要先找到後綴結點再根據“str的下一個字符”這樣一條邊找到下一個結點，現在可以直接通過當前結點的“str的下一個字符”這樣一條邊就可以接著往下匹配了，如果本來是有這條邊的，那不用多說，而如果這條邊是根據後綴結點補全的，那便是我們想要的結果！”

“所以呢！完成這個任務的方法總的來說就是這樣，先根據字典構建一棵Trie樹，然後根據我們之前所說的構建出對應的Trie圖，然後從Trie圖的根節點開始，沿著文章str的每一個字符，走出對應的邊，直到遇到一個標記結點或者整個str都已經匹配完成了~”小Hi適時的總結道。

“而這樣的時間復雜度則在O(NL+M)級別的呢！想來是足以完成河蟹先生的要求了呢~”小Ho搬了搬手指，說道。

“是的！但是河蟹先生要求的可不是想法哦，他可是希望我們寫出程序給它呢！”

Input

每個輸入文件有且僅有一組測試數據。

每個測試數據的第一行為一個整數N，表示河蟹詞典的大小。

接下來的N行，每一行為一個由小寫英文字母組成的河蟹詞語。

接下來的一行，為一篇長度不超過M，由小寫英文字母組成的文章。

對於60%的數據，所有河蟹詞語的長度總和小於10, M<=10

對於80%的數據，所有河蟹詞語的長度總和小於10^3, M<=10^3

對於100%的數據，所有河蟹詞語的長度總和小於10^6, M<=10^6, N<=1000

Output

對於每組測試數據，輸出一行"YES"或者"NO"，表示文章中是否含有河蟹詞語。

Sample Input

6
aaabc
aaac
abcc
ac
bcd
cd
aaaaaaaaaaabaaadaaac

Sample Output

YES

說明：

設 i 父節點為 i‘，i的入邊上的字母為 c。

一個顯然的結論是，如果 fail(i?′??) 有字母 c 的出邊，則該出邊指向的點即為 fail(i)。
例如，上圖中 fail(7)=1,fail(8)=2。

如果 fail(i?′??) 沒有字母 c 的出邊，則沿著失配函數繼續向上找，找到 fail(fail(i?′??)) …… 直到找到根為止，如果找不到一個符合條件的節點，則 fail(i) 為根。
例如，上圖中 fail(3)=0。

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1000005;

struct Trie{
    bool flag;
    struct Trie* nxt[26];
    struct Trie* behind;
};

int main()
{
	//freopen("input.txt","r",stdin); 
    char str[maxn];
    int N;
    Trie* root = new Trie;
    for (int i = 0;i < 26;i++)
    {
        root->nxt[i] = NULL;
    }
    root->behind = NULL;
    root->flag = false;
    scanf("%d",&N);
    while (N--)
    {
        scanf("%s",str);
        Trie* p = root;
        int i = 0;
        while (str[i])
        {
            int j = str[i] - ‘a‘;
            if (!p->nxt[j])
            {
                Trie* q = new Trie;
                for (int k = 0;k < 26;k++)  q->nxt[k] = NULL;
                q->behind = NULL;
                q->flag = false;
                p->nxt[j] = q;
            }
            p = p->nxt[j];
            i++;
        }
        p->flag = true;
    }
    queue<Trie*>que;
    root->behind = root;
    for (int i = 0;i < 26;i++)
    {
        if (!root->nxt[i])
        {
            root->nxt[i] = root;
        }
        else
        {
            root->nxt[i]->behind = root;
            que.push(root->nxt[i]);
        }
    }

    while (!que.empty())
    {
        Trie* p = que.front();
        Trie* q = p->behind;
        que.pop();
        for (int i = 0;i < 26;i++)
        {
            if (!p->nxt[i])
            {
                p->nxt[i] = q->nxt[i];
            }
            else
            {
                p->nxt[i]->behind = q->nxt[i];
                que.push(p->nxt[i]);
            }
        }
    }
    char article[maxn];
    Trie* p = root;
    scanf("%s",article);
    int i = 0;
    bool tag = false;
    while (article[i])
    {
        int j = article[i] - ‘a‘;
        p = p->nxt[j];
        if (p->flag)
        {
            tag = true;
            printf("YES\n");
            break;
        }
        i++;
    }
    if (!tag)   printf("NO\n");
    return 0;
}

提示

提示一：

“還記得我們在第二周時，是如何使用Trie樹解決字符串自動補全問題的麽？”小Hi如是問道。

“還記得，就是對於每一個詢問，根據其每個位置上的字符，在Trie樹上走出對應的邊！”小Ho的記憶力還是挺不錯的，很快便答了上來。

小Hi滿意的點了點頭，繼續問道：“那你想想怎麽用Trie樹來解決河蟹先生交代的任務？”

“好的！”小Ho滿口答應，隨即分析道：“現在的這個問題和第二周遇到的問題的不同之處在於，第二周時一定是從詢問的第一個字符開始匹配，然後找出所有可能的匹配，而我們現在遇到的問題是可以從詢問的任意一個位置開始匹配，看是否會在Trie樹上走到一個標記結點（標記結點對應路徑為一個屬於詞典的單詞）。”

“沒錯，那你準備怎麽做呢？”

“我準備對於螃蟹先生給我的文章，還是像之前我們相出的樸素算法那樣，枚舉一個起始位置，然後我們的問題就變成了：是否從這個起始位置開始的一段字符（也就是從這個起始位置開始的字符串的一個前綴字符串），它存在於“河蟹”詞典裏面 ？而這個問題，就和第二周的問題幾乎一樣了，唯一不同的是，我是要一直在Trie樹中走下去直到無邊可走，或者走到一個標記結點的時候才能夠停下來，前者代表沒有任何需要河蟹的單詞，後者則說明我們找到了。”小Ho井井有條的分析道。

“也就是說，第二周我們成功解決了計算前綴匹配的數量這樣一個問題，而這一周的任務卻是可以在任意位置匹配，所以我們就枚舉一個起始點，將這個問題轉化成前綴匹配這樣一個我們已知的問題來做，這樣的思路麽？”小Hi總結道。

“嗯！我就是這麽想的~”小Ho道。

“嗯，這個方法聽起來挺有意思的，而且仔細分析一下，這樣做所需要的計算次數會在M*L這個數量級上，比我們之前的樸素算法已經好了很多呢~”小Hi誇獎了一番。

“嘿嘿，但是你之前說的Trie圖是怎麽回事，它又能將計算次數縮減到怎樣的數量級呢？”小Ho的好奇心也是燃燒了起來。

“且聽我說~”

提示二：

“你看這組輸入——文章str、詞典dic還有我們構建的Trie樹tree，我們在算法過程中，先枚舉第一個字符作為起始位置，並最多匹配到第k個字符，因為str[1..k]這一段在tree中對應的結點A結點沒有str[k+1]這一條邊。這時候我們便要枚舉第二個字符作為起始位置，並最多匹配到第k2個字符，這同樣是因為str[2..k2]這一段在tree中對應的結點B結點沒有str[k2+1]這一條邊。也就是說我們在最開始的計算中，要先從tree的0號結點走到A結點，然後回到0號結點，再走到B結點。”小Hi在黑板上畫了一些奇奇怪怪的符號，對小Ho如是解說道。

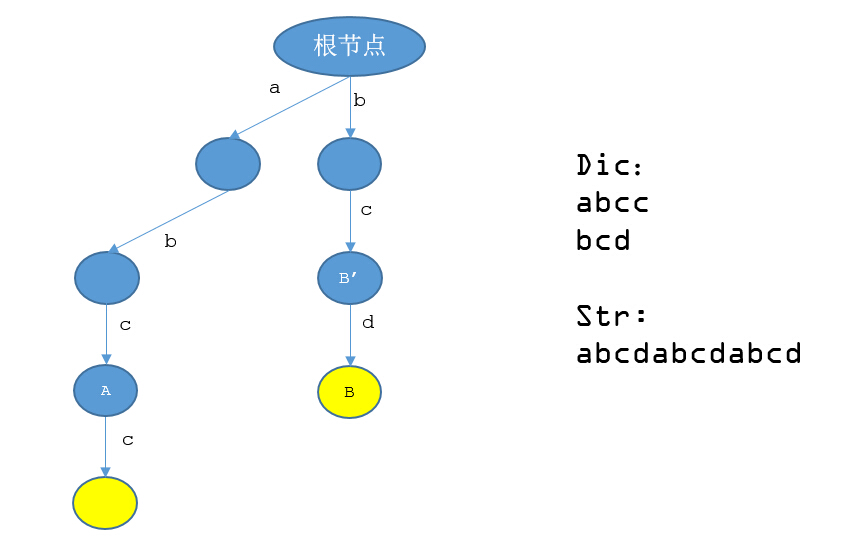
“是的！等等，我怎麽覺得這裏似曾相識呢？”小Ho奇道。

“問得好~那麽你覺不覺得這個過程和上一周的KMP算法很相似，都是枚舉原串（文章、str）的起始位置，然後在模式串（Trie樹）中依次進行匹配？”小Hi說道。

“是的！不同之處就在於模式串就是在一個數組裏一個個匹配下來，而Trie樹則是在一個樹結構中一個個順著邊走~這無非就是單個詞語和多個詞語的差別了是麽？”小Ho也是一點就透。

“沒錯！那我們再回想一下我們當時是怎麽優化KMP的——我們既然已經從str的當前起點i開始匹配了l個長度，那麽在枚舉str的下一個起點i+1的時候，就意味著最開始的l-1個字符都已經在之前的計算中匹配過了，如果我們能夠利用好這個信息的話，就能夠大大的減少時間復雜度。”

“換句話說，如果我們從str的當前起點開始，匹配了l個長度走到了A結點，如果我們把A結點對應的字符串（即從tree的0號走到A結點的路徑）去掉第一個字符，形成一個新的字符串，那麽這個字符串肯定是和從str的下一個起點開始，長度為l-1的子串是一樣的，而如果我們能夠預先找到這個字符串在tree中對應的結點B‘，我們就不用像之前所說的那樣從0號節點走到A結點然後回到0號結點再走到B結點，而是可以直接從0號結點走到A結點然後直接跳轉到B’結點然後再根據從str[i+l..k1]這一段走到B結點！”小Hi一口氣說道，頓時感覺口幹舌燥，於是拿起了一旁的杯子，猛灌了一口涼開水。

”哦！那麽如果用之前的這個例子的話，從str的第一個位置開始，匹配了3個字符走到了A結點，對應的字符串是abc，如果第一個字符a去掉變成bc，這個字符和從str的第二個位置開始長度為2的字串bc的確是一樣的，此時bc在tree中對應的結點是B‘結點，所以我們用之前的算法的話就是從0號結點走到A結點，然後再從0號結點走到B結點，現在可以直接從A結點走到B‘結點，然後根據str的第4（i+l=1+3）個字符走到B結點！”小Ho趁著小Hi休息的功夫，也是拿起了之前小Hi給出的例子推演道。”

“沒錯！所以我們的問題規約成了：如何對於一棵給定的Trie樹，找到其中每一個結點對應的後綴結點——這個結點在Trie中對應路徑去掉第一個字符之後在Trie中對應的結點。“小Hi擦了把汗，感覺舒爽許多，於是繼續說道。

“我大致懂了！這個後綴結點就和我們在KMP算法中求解的NEXT數組是一個意思！”小Ho開心道。

“你真聰明~”小Hi誇獎道。

提示三：

“先看之前你說的那個例子，如果tree中存在一個結點D，其對應的路徑是aabc，那麽這個結點的後綴結點是哪一個？”小Hi問道。

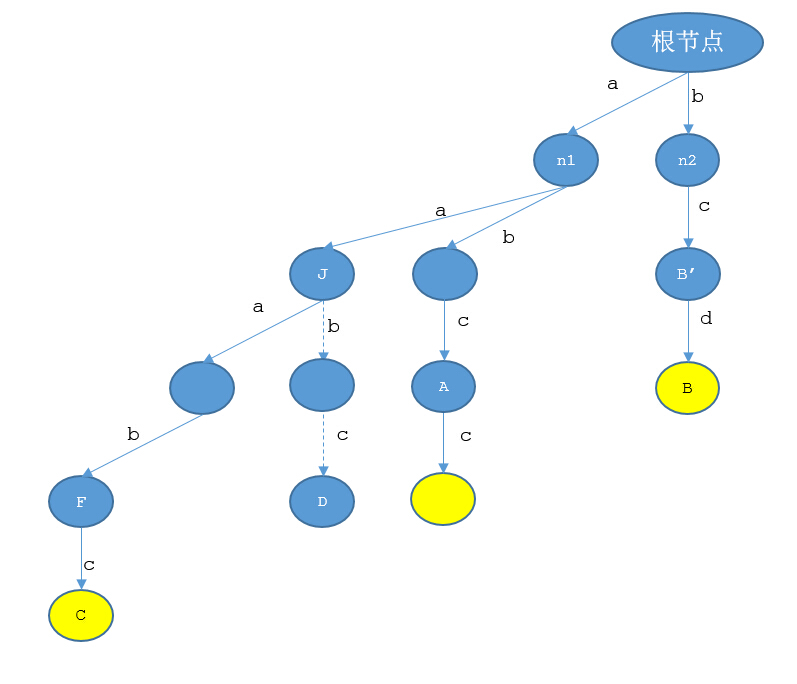
“aabc……去掉第一個字符就是abc，對應的是A結點，所以D結點的後綴結點是A！”小Ho很快便做出了回答。

“那麽問題不就簡單了麽，既然結點D是不存在的，那麽不就意味著這個開始結點的枚舉，是肯定在中途就要找不到實際上是沒有意義的麽，直接從C結點跳轉到A結點就可以了！所以只需要令C結點的後綴結點是A結點，像D結點這種不存在的結點當然要視為冗余計算，扔掉就行了！”小Hi老師斬釘截鐵道。

“D結點好可憐……但是，如果從tree的根節點到D結點的路徑中有標記結點怎麽辦？這樣的跳過會不會導致標記結點被忽略掉了？”小Ho問道。

“如果不註意的話是會的呢！這就要引進一個新的概念，後綴結點為標記結點的結點也需要被標記，比如像對應路徑為aab的E結點就是標記點對麽？而aaab對應的F結點的後綴結點便是E結點，所以需要對F結點進行標記，這樣在走到F結點的時候，就知道已經匹配出了一個河蟹詞語了呢。”小Hi耐心答道。

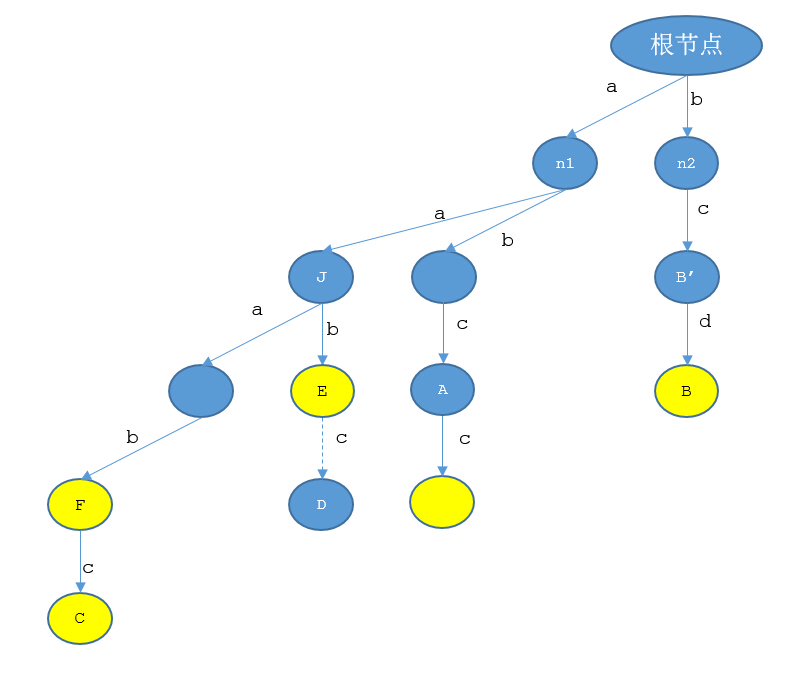
“那麽接下來就開始說怎麽快速有效的求後綴結點！小Ho，你先回答我：樹結構最大的特點是什麽？”小Hi問道。

“是遞歸結構！”小Ho想也沒想就回答道。

“真聰明！雖然是導演安排好的臺詞，但是回答速度真是一流呢！”小Hi點了點頭，繼續說道：“所以我們想要求Trie樹種每個結點的後綴結點，最直觀的方法也就是像當初我們求解KMP的NEXT數組時那種從左到右的拓撲順序一樣，從根節點開始，以寬度優先遍歷的順序，依次求解每一個結點的後綴結點。”

“嗯！這樣可以保證每個結點對應的後綴結點，由於其對應字符串長度一定至少少1，所以一定會在它之前得到計算？但是這樣有什麽用呢？誒，我想到一個，這樣就可以知道它的後綴結點是不是標記結點了，從而決定自己是不是要被標記是麽？”小Ho決定打破砂鍋問到底。

“別急！聽我慢慢說來。”小Hi不知從哪摸出一把羽扇，扇了兩下，問道：“你看這棵Trie樹，根節點的後綴結點是哪個？”

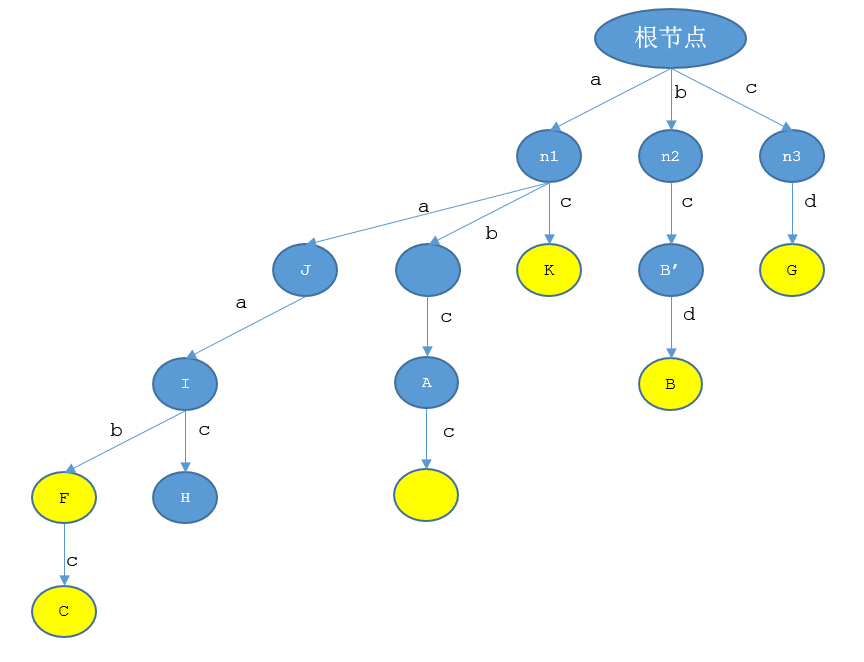
”根節點對應的字符串是空，去掉第一個字符……還是空，所以就是根節點自己了是吧？”小Ho想了想，說道。

“是的，那你看從根節點連出去的這三個點n1,n2,n3他們的後綴結點是哪個？”小Hi繼續問道。

“他們對應的字符串都只有一個字符，所以去掉一個字符就變成空了，於是他們的後綴結點也都是根節點。”小Ho也繼續答道。

“那麽現在，假設所有深度小於B結點的結點的後綴結點都已經算出來了，我想要算B結點的後綴結點，有沒有什麽好的方法呢？”小Hi隨手填了幾個結點的後綴結點，向小Ho問道。

“如果考慮遞歸的思路的話，B結點的父親結點是對應字符串為bc的B‘結點，B‘結點的後綴結點是n3結點，所以從B‘結點出發經‘d‘這樣一條邊到達的結點B的後綴結點自然應該就是從B‘結點的後綴結點n3出發經‘d‘這樣一條邊到達的結點——G結點了！”小Ho仔細研究了下，答道。”這麽說來，是不是所有結點都可以這麽求呀，如果它父親結點是通過編號為char的一條邊走向它的，那麽只要找到它父親的後綴結點，並且走出編號為char的一條邊，就能夠找到它的後綴結點了？”

“差不多就是這個思路呢！但是你有沒有想過如果它父親結點的後綴結點並沒有編號為char的一條邊，你該怎麽辦？”小Hi也是不厭其煩，繼續問道。

“我想想，比如說結點G的父親結點I的後綴結點J沒有‘c‘這樣一條邊，但是結點J的後綴結點n1卻有‘c‘這樣一條邊，由於後綴結點每次都是去掉前幾個字符，所以後綴結點的後綴結點也相當於是“弱”一點的後綴結點，在沒有更好的選擇的情況下（因為這是第一次找到的有‘c‘這樣一條邊的後綴結點），G的後綴結點就應該是結點K了吧！”小Ho仔細想想，答道。

“你這樣的話，會不會覺得，每次都要往回不停的找後綴結點，挺浪費時間的呢？”這下子換到小Hi打破砂鍋問到底了。

“那該怎麽辦？”小Ho也是沒轍了。

“你看看這麽做怎麽樣，我還是按照寬度優先搜索的順序遍歷整棵樹，對於每一個結點，我不僅僅要求出它的後綴結點，我還要求出到達這個點後，經由每一個char（比如‘a‘..‘d‘）會走到的結點。由於到達這個結點之後，所有深度比它小的結點的這些值都算出來了，於是我可以直接通過父親節點的後綴結點經由“父親節點走到當前結點經過的邊”走到的結點來計算我的後綴結點，同時這個後綴結點所要計算的值也都計算出來了，所以我可以通過這個後綴結點經由每一個char（比如‘a‘..‘d‘）會走到的結點來計算我經由每一個char（比如‘a‘..‘d‘）會走到的結點。”小Hi大致的說了一下思路。

“小Hi老師，我聽暈了！”小Ho報告說。

“這個簡單，我就拿這個例子給你依次算一算。”

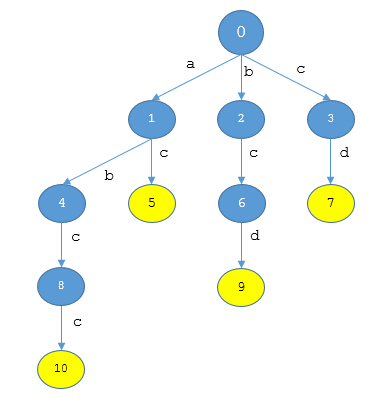
“如果用trie(X)表示X的根節點，next(X)(‘a‘)表示從X出發標號為‘a‘的邊指向的結點，我們可以知道trie(0)=0, next(0)(‘a‘)=1, next(0)(‘b‘)=2, next(0)(‘c‘)=3, next(0)(‘d‘)=0。”

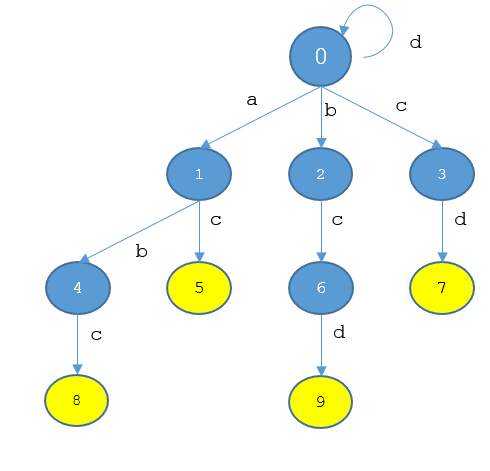
“由於trie(1)=0, 我們可以補上從1出發的‘a‘,‘d‘這兩條邊：next(1)(‘a‘)=next(0)(‘a‘)=1, next(1)(‘d‘)=next(0)(‘d‘)=0”

“由於trie(2)=0, 我們可以補上從2出發的‘a‘,‘b‘,‘d‘這三條邊：next(2)(‘a‘)=next(0)(‘a‘)=1, next(2)(‘b‘)=next(0)(‘b‘)=2, next(2)(‘d‘)=next(0)(‘d‘)=0”

“由於trie(2)=0, 我們可以補上從3出發的‘a‘,‘b‘,‘c‘這三條邊：next(3)(‘a‘)=next(0)(‘a‘)=1, next(3)(‘b‘)=next(0)(‘b‘)=2, next(2)(‘c‘)=next(0)(‘c‘)=3”

“由於trie(4)=next(trie(1))(‘b‘)=2, 我們可以補上從4出發的‘a‘,‘b‘,‘d‘這三條邊：next(4)(‘a‘)=next(2)(‘a‘)=1, next(4)(‘b‘)=next(2)(‘b‘)=2, next(4)(‘d‘)=next(2)(‘d‘)=0”

“由於trie(5)=next(trie(1))(‘c‘)=3, 我們可以補上從5出發的‘a‘,‘b‘,‘c‘,‘d‘這四條邊：next(5)(‘a‘)=next(3)(‘a‘)=1, next(5)(‘b‘)=next(3)(‘b‘)=2, next(5)(‘c‘)=next(3)(‘c‘)=3, next(5)(‘d‘)=next(3)(‘d‘)=7”

“由於trie(6)=next(trie(2))(‘c‘)=3, 我們可以補上從6出發的‘a‘,‘b‘,‘c‘這三條邊：next(6)(‘a‘)=next(3)(‘a‘)=1, next(6)(‘b‘)=next(3)(‘b‘)=2, next(6)(‘c‘)=next(3)(‘c‘)=3”

“由於trie(7)=next(trie(3))(‘d‘)=0, 我們可以補上從7出發的‘a‘,‘b‘,‘c‘,‘d‘這四條邊：next(7)(‘a‘)=next(0)(‘a‘)=1, next(7)(‘b‘)=next(0)(‘b‘)=2, next(7)(‘c‘)=next(0)(‘c‘)=3, next(7)(‘d‘)=next(0)(‘d‘)=0”

“由於trie(8)=next(trie(4))(‘c‘)=6, 我們可以補上從8出發的‘a‘,‘b‘,‘c‘,‘d‘這四條邊：next(8)(‘a‘)=next(6)(‘a‘)=1, next(8)(‘b‘)=next(6)(‘b‘)=2, next(8)(‘c‘)=next(6)(‘c‘)=3, next(8)(‘d‘)=next(6)(‘d‘)=9”

“由於trie(9)=next(trie(6))(‘d‘)=7, 我們可以補上從9出發的‘a‘,‘b‘,‘c‘,‘d‘這四條邊：next(9)(‘a‘)=next(7)(‘a‘)=1, next(9)(‘b‘)=next(7)(‘b‘)=2, next(9)(‘c‘)=next(7)(‘c‘)=3, next(9)(‘d‘)=next(7)(‘d‘)=0”

“此時這個圖已經變得過於復雜了，我就不畫出來了，但是我想你已經可以從我上面所說的知道每個節點的後綴結點了呢！”小Hi道。

hihocoder 1036 Trie圖（AC自動機）