elements 利用 rep 等於 pre sum 要求 chan each

date：公元2017年7月19日適逢周三； location：清北集訓 杭州 point：二維樹狀數組/二維差分 Matrix

Time Limit: 3000MS		Memory Limit: 65536K
Total Submissions: 28325		Accepted: 10341

Description

Given an N*N matrix A, whose elements are either 0 or 1. A[i, j] means the number in the i-th row and j-th column. Initially we have A[i, j] = 0 (1 <= i, j <= N).

We can change the matrix in the following way. Given a rectangle whose upper-left corner is (x1, y1) and lower-right corner is (x2, y2), we change all the elements in the rectangle by using "not" operation (if it is a ‘0‘ then change it into ‘1‘ otherwise change it into ‘0‘). To maintain the information of the matrix, you are asked to write a program to receive and execute two kinds of instructions.

1. C x1 y1 x2 y2 (1 <= x1 <= x2 <= n, 1 <= y1 <= y2 <= n) changes the matrix by using the rectangle whose upper-left corner is (x1, y1) and lower-right corner is (x2, y2).
2. Q x y (1 <= x, y <= n) querys A[x, y].

Input

The first line of the input is an integer X (X <= 10) representing the number of test cases. The following X blocks each represents a test case.

The first line of each block contains two numbers N and T (2 <= N <= 1000, 1 <= T <= 50000) representing the size of the matrix and the number of the instructions. The following T lines each represents an instruction having the format "Q x y" or "C x1 y1 x2 y2", which has been described above.

Output

For each querying output one line, which has an integer representing A[x, y].

There is a blank line between every two continuous test cases.

Sample Input

1
2 10
C 2 1 2 2
Q 2 2
C 2 1 2 1
Q 1 1
C 1 1 2 1
C 1 2 1 2
C 1 1 2 2
Q 1 1
C 1 1 2 1
Q 2 1

Sample Output

1
0
0
1

Source

POJ Monthly,Lou Tiancheng 題目翻譯（有道滋滋） 給一個N * N矩陣,其元素是0或1。(i,j)意味著i行和j列數。一開始我們有一個(i,j)= 0(1 < = i,j < = N)。

我們可以改變矩陣以以下方式。給定一個矩形的左上角(x1,y1),右下角(x2,y2),我們改變矩形中的所有元素用“不”操作(如果它是一個‘ 0 ‘然後改變它為‘ 1 ‘否則改變成“0”)。保持矩陣的信息,你被要求寫一個程序接收和執行兩種指令。

1。C(x1,y1 x2 y2 x1 < = x2(1 < = < = n,1 < = y1 < = y2 < = n)變化矩陣,利用矩形的左上角(x1,y1),右下角(x2,y2)。
2。Q x y(1 < = x,y < = n)查詢(x,y)。

輸入

輸入的第一行是一個整數X(X < = 10)代表測試用例的數量。以下X塊每個表示一個測試用例。

每一塊的第一行包含兩個數N和T(2 < = N < = 1000,1 < = T < = 50000)代表矩陣的大小和數量的指示。以下T行每個代表一個指令的格式“Q x y”或“C x1 y1 x2 y2”,上面所描述的。

輸出

為每個查詢輸出一行,一個整數代表一個(x,y)。

之間有一個空行每兩個連續的測試用例。

樣例輸入

1
2 10
C 2 1 2 2
Q 2 2
C 2 1 2 1
Q 1 1
C 1 1 2 1
C 1 2 1 2
C 1 1 2 2
Q 1 1
C 1 1 2 1
Q 2 1

樣例輸出

1
0
0
1

題解：據說本題是用數學方法來做，但是oycy大學霸+lsh大學霸好像在我寫這篇題解之前已經研究了2個小時了……
這裏共享我的解題方法：
再說那天的數學聽得我對數學沒有信心了，所以壓根就沒想到數學；
不是說數學不可以，但是太過困難了（深切感受），
一想到數學便睡意襲來，
在睡了一會兒後，小人不才，大概花了40分鐘便想出一個基於二維樹狀數組的思路：
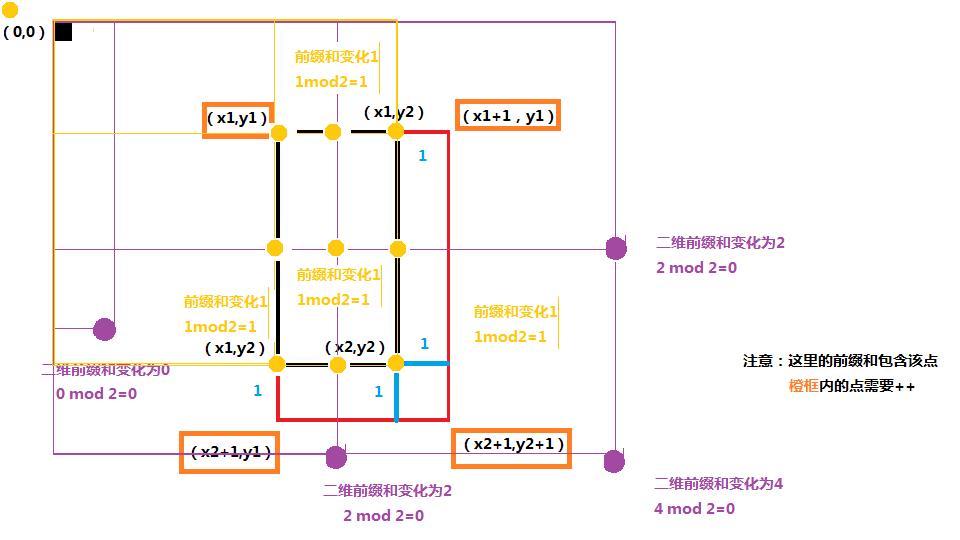
現在我們設需要not變換的子矩陣左上坐標為(x1,y1)右下坐標(x2,y2)
不妨拓展1格，方便我們解題，先看到一幅圖（拓展後）
註意到左上方有一個小黃人（這沒什麽用，請自行過濾）
黑方框為(0,0)

黑方框代表我們需要not的區域 紅方框代表拓展出來的區域
TIPS:紅方框邊界上的點沒畫（lazy++），自己推吧，懶得畫了，符合的。
在我的解題方案中，我們只要將點（橙框的4點）++
a[x1,y1]++
a[x2+1,y1]++
a[x1+1,y1]++
a[x2+1,y2+1]++
可以證明在黑方框外的任一點的二維前綴和是增量r mod 2 恒等於 0
而黑方框內的任一點的二維前綴和的增量r mod 2 恒等於 1
二維前綴和的最快維護方案是二維樹狀數組；具體維護不在多講（本質是為樹狀數組+循環）
這樣我們只要使4個點的權值++，維護前綴和，求Q(x,y)只要C(x,y)mod 2=1 則最終的點(x,y)就是1，反之就是0
做完了~~
用not 來維護樹狀數組你就中陷阱了；
或者用dp來做，也是行不通的；

希望lsh+oycy大學霸orz能夠早日用數學AC本題！

代碼:

uses math;
var n,m,i,j,t,x1,x2,y1,y2,q,x,y,tt,ii:longint;
    c:array[0..1000,0..1000]of longint;
    ch:char;
function lowbit(x:longint):longint;
begin
 exit(x and (-x));
end;
procedure update(xx,yy,opx:longint);//二維樹狀數組把數組中a[xx]+yy並且跟新樹狀數組c[]
var ty,x,y:longint;
begin
 x:=xx; y:=yy;
 ty:=yy;
  while x<=n do begin
   y:=ty;
   while y<=n do begin
    c[x,y]:=c[x,y]+opx;
    y:=y+lowbit(y);
   end;
   x:=x+lowbit(x);
  end;
end;
function query(x,y:longint):longint;//詢問a二維矩陣a[]前綴和
var  sum,ty:longint;
begin
 sum:=0;
 ty:=y;
 while x>0 do begin
  y:=ty;
  while y>0 do begin
   sum:=sum+c[x,y];
   y:=y-lowbit(y);
  end;
  x:=x-lowbit(x);
 end;
 exit(sum);
end;
begin
readln(tt);//tt組數據
for ii:=1 to tt do begin
 readln(n,q);//n*n矩陣，q個操作
 for i:=1 to q do begin
  read(ch);//ch為指示符
  case ch of
   ‘C‘:begin readln(x1,y1,x2,y2);
      update(x1,y1,1);   update(x1,y2+1,1);
      update(x2+1,y1,1); update(x2+1,y2+1,1);//4個橙色的點依次更改
   end;
   ‘Q‘:begin readln(x,y); writeln(query(x,y) mod 2);end;//判斷mod 2？=1
  end;
 end;
 writeln;
 end;
end.

我們來計算時間復雜度：

對於1次程序tt++前完成，q個詢問，

如果是Q則復雜度是O(log n) 如果是C則復雜度為O(4 log n)，最壞時間復雜度為O(4 log n)

那麽對於1次完整的解決，我們最壞的時間復雜度為O (4q log n)

對於完整的tt次解決，最壞的時間復雜度是O(4*q*tt*log n)

2 <= N <= 1000, 1 <= q<= 50000; tt<=10;

那麽最壞情況的常數為O(4*50000*10*10)=O(2000w)

沒有超時，完美解決！

希望lsh+oycy大學霸orz能夠早日用數學AC本題！

POJ 2155 Matrix (矩形)