簡單 此外 urn csdn bsp center sum 又能 超出

轉自：數據標準化/歸一化normalization

這裏主要講連續型特征歸一化的常用方法。離散參考[數據預處理：獨熱編碼（One-Hot Encoding）]。

基礎知識參考：

[均值、方差與協方差矩陣 ]

[矩陣論：向量範數和矩陣範數 ]

數據的標準化（normalization）和歸一化

數據的標準化（normalization）是將數據按比例縮放，使之落入一個小的特定區間。在某些比較和評價的指標處理中經常會用到，去除數據的單位限制，將其轉化為無量綱的純數值，便於不同單位或量級的指標能夠進行比較和加權。其中最典型的就是數據的歸一化處理，即將數據統一映射到[0,1]區間上。

目前數據標準化方法有多種，歸結起來可以分為直線型方法(如極值法、標準差法)、折線型方法(如三折線法)、曲線型方法(如半正態性分布)。不同的標準化方法，對系統的評價結果會產生不同的影響，然而不幸的是，在數據標準化方法的選擇上，還沒有通用的法則可以遵循。

歸一化的目標

1 把數變為（0，1）之間的小數
主要是為了數據處理方便提出來的，把數據映射到0～1範圍之內處理，更加便捷快速，應該歸到數字信號處理範疇之內。
2 把有量綱表達式變為無量綱表達式
歸一化是一種簡化計算的方式，即將有量綱的表達式，經過變換，化為無量綱的表達式，成為純量。 比如，復數阻抗可以歸一化書寫：Z = R + jωL = R(1 + jωL/R) ，復數部分變成了純數量了，沒有量綱。
另外，微波之中也就是電路分析、信號系統、電磁波傳輸等，有很多運算都可以如此處理，既保證了運算的便捷，又能凸現出物理量的本質含義。

歸一化後有兩個好處

1. 提升模型的收斂速度

如下圖，x₁的取值為0-2000，而x₂的取值為1-5，假如只有這兩個特征，對其進行優化時，會得到一個窄長的橢圓形，導致在梯度下降時，梯度的方向為垂直等高線的方向而走之字形路線，這樣會使叠代很慢，相比之下，右圖的叠代就會很快（理解：也就是步長走多走少方向總是對的，不會走偏）

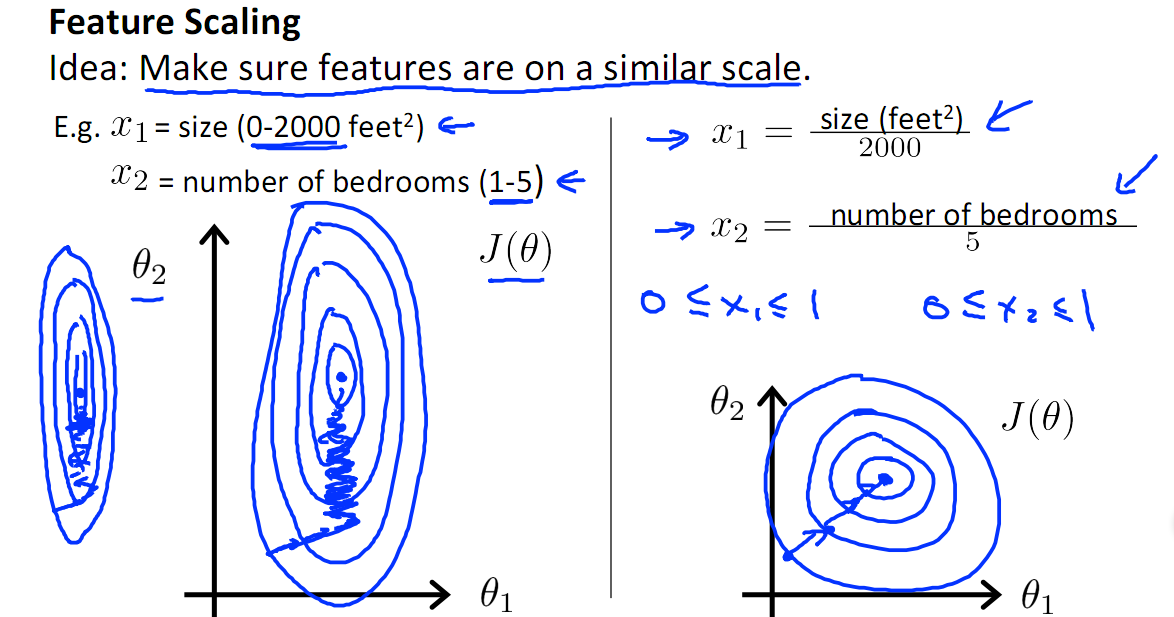
2.提升模型的精度

歸一化的另一好處是提高精度，這在涉及到一些距離計算的算法時效果顯著，比如算法要計算歐氏距離，上圖中x2的取值範圍比較小，涉及到距離計算時其對結果的影響遠比x1帶來的小，所以這就會造成精度的損失。所以歸一化很有必要，他可以讓各個特征對結果做出的貢獻相同。

在多指標評價體系中，由於各評價指標的性質不同，通常具有不同的量綱和數量級。當各指標間的水平相差很大時，如果直接用原始指標值進行分析，就會突出數值較高的指標在綜合分析中的作用，相對削弱數值水平較低指標的作用。因此，為了保證結果的可靠性，需要對原始指標數據進行標準化處理。

在數據分析之前，我們通常需要先將數據標準化（normalization），利用標準化後的數據進行數據分析。數據標準化也就是統計數據的指數化。數據標準化處理主要包括數據同趨化處理和無量綱化處理兩個方面。數據同趨化處理主要解決不同性質數據問題，對不同性質指標直接加總不能正確反映不同作用力的綜合結果，須先考慮改變逆指標數據性質，使所有指標對測評方案的作用力同趨化，再加總才能得出正確結果。數據無量綱化處理主要解決數據的可比性。經過上述標準化處理，原始數據均轉換為無量綱化指標測評值，即各指標值都處於同一個數量級別上，可以進行綜合測評分析。

從經驗上說，歸一化是讓不同維度之間的特征在數值上有一定比較性，可以大大提高分類器的準確性。

數據需要歸一化的機器學習算法

需要歸一化的模型：

有些模型在各個維度進行不均勻伸縮後，最優解與原來不等價，例如SVM（距離分界面遠的也拉近了，支持向量變多？）。對於這樣的模型，除非本來各維數據的分布範圍就比較接近，否則必須進行標準化，以免模型參數被分布範圍較大或較小的數據dominate。
有些模型在各個維度進行不均勻伸縮後，最優解與原來等價，例如logistic regression（因為θ的大小本來就自學習出不同的feature的重要性吧？）。對於這樣的模型，是否標準化理論上不會改變最優解。但是，由於實際求解往往使用叠代算法，如果目標函數的形狀太“扁”，叠代算法可能收斂得很慢甚至不收斂。所以對於具有伸縮不變性的模型，最好也進行數據標準化。

不需要歸一化的模型：

ICA好像不需要歸一化（因為獨立成分如果歸一化了就不獨立了？）。

基於平方損失的最小二乘法OLS不需要歸一化。

[線性回歸與特征歸一化(feature scaling)]

皮皮blog

常見的數據歸一化方法

min-max標準化(Min-max normalization)/0-1標準化(0-1 normalization)

也叫離差標準化，是對原始數據的線性變換，使結果落到[0,1]區間，轉換函數如下：

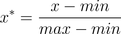
其中max為樣本數據的最大值，min為樣本數據的最小值。

def Normalization(x):
return [(float(i)-min(x))/float(max(x)-min(x)) for i in x]

如果想要將數據映射到[-1,1]，則將公式換成：

x?=x?xmeanxmax?xmin

x_mean表示數據的均值。

def Normalization2(x):
return [(float(i)-np.mean(x))/(max(x)-min(x)) for i in x]

這種方法有一個缺陷就是當有新數據加入時，可能導致max和min的變化，需要重新定義。

log函數轉換

通過以10為底的log函數轉換的方法同樣可以實現歸一下，具體方法如下：

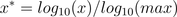
看了下網上很多介紹都是x*=log10(x)，其實是有問題的，這個結果並非一定落到[0,1]區間上，應該還要除以log10(max)，max為樣本數據最大值，並且所有的數據都要大於等於1。

atan函數轉換

用反正切函數也可以實現數據的歸一化。

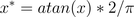
使用這個方法需要註意的是如果想映射的區間為[0,1]，則數據都應該大於等於0，小於0的數據將被映射到[-1,0]區間上，而並非所有數據標準化的結果都映射到[0,1]區間上。

z-score 標準化(zero-mean normalization)

最常見的標準化方法就是Z標準化，也是SPSS中最為常用的標準化方法，spss默認的標準化方法就是z-score標準化。

也叫標準差標準化，這種方法給予原始數據的均值（mean）和標準差（standard deviation）進行數據的標準化。

經過處理的數據符合標準正態分布，即均值為0，標準差為1，其轉化函數為：

x?=x?μσ

其中μ為所有樣本數據的均值，σ為所有樣本數據的標準差。

z-score標準化方法適用於屬性A的最大值和最小值未知的情況，或有超出取值範圍的離群數據的情況。

標準化的公式很簡單，步驟如下

　　1.求出各變量（指標）的算術平均值（數學期望）xi和標準差si ；
　　2.進行標準化處理：
　　zij=（xij－xi）/si
　　其中：zij為標準化後的變量值；xij為實際變量值。
　　3.將逆指標前的正負號對調。
　　標準化後的變量值圍繞0上下波動，大於0說明高於平均水平，小於0說明低於平均水平。

def z_score(x, axis):
    x = np.array(x).astype(float)
    xr = np.rollaxis(x, axis=axis)
    xr -= np.mean(x, axis=axis)
    xr /= np.std(x, axis=axis)
    # print(x)
    return x

為什麽z-score 標準化後的數據標準差為1?

x-μ只改變均值，標準差不變，所以均值變為0

(x-μ)/σ只會使標準差除以σ倍，所以標準差變為1

皮皮blog

Decimal scaling小數定標標準化

這種方法通過移動數據的小數點位置來進行標準化。小數點移動多少位取決於屬性A的取值中的最大絕對值。

將屬性A的原始值x使用decimal scaling標準化到x‘的計算方法是：
x‘=x/(10^j)
其中，j是滿足條件的最小整數。
例如 假定A的值由-986到917，A的最大絕對值為986，為使用小數定標標準化，我們用每個值除以1000（即，j=3），這樣，-986被規範化為-0.986。
註意，標準化會對原始數據做出改變，因此需要保存所使用的標準化方法的參數，以便對後續的數據進行統一的標準化。

Logistic/Softmax變換

logistic函數和標準正態函數

新數據=1/（1+e^(-原數據)）

P(i)=11+exp(?θTix)

這個函數的作用就是使得P(i)在負無窮到0的區間趨向於0，在0到正無窮的區間趨向於1。同樣，函數（包括下面的softmax）加入了e的冪函數正是為了兩極化：正樣本的結果將趨近於1，而負樣本的結果趨近於0。這樣為多類別分類提供了方便（可以把P(i)看作是樣本屬於類別i的概率）。

logit(P) = log(P / (1-P)) = a + b*x 以及 probit(P) = a + b*x 這兩個連接函數的性質使得P的取值被放大到整個實數軸上。 事實上可以把上面的公式改寫一下： P = exp(a + b*x) / (1 + exp(a + b*x)) 或者 P = pnorm(a + b*x)（這個是標準正態分布的分布函數）

Note: 上半部分圖形顯示了概率P隨著自變量變化而變化的情況，下半部分圖形顯示了這種變化的速度的變化。可以看得出來，概率P與自變量仍然存在或多或少的線性關系，主要是在頭尾兩端被連接函數扭曲了，從而實現了[0,1]限制。同時，自變量取值靠近中間的時候，概率P變化比較快，自變量取值靠近兩端的時候，概率P基本不再變化。這就跟我們的直觀理解相符合了，似乎是某種邊際效用遞減的特點。

[logistic回歸的一些直觀理解(1.連接函數 logit probit)]

Softmax函數

是logistic函數的一種泛化，Softmax是一種形如下式的函數：

假設我們有一個數組，V，Vi表示V中的第i個元素，那麽這個元素的Softmax值就是

也就是說，是該元素的指數，與所有元素指數和的比值

為什麽要取指數，第一個原因是要模擬 max 的行為，所以要讓大的更大。第二個原因是需要一個可導的函數。

通過softmax函數，可以使得P(i)的範圍在[0,1]之間。在回歸和分類問題中，通常θ是待求參數，通過尋找使得P(i)最大的θi作為最佳參數。

此外Softmax函數同樣可用於非線性估計，此時參數θ可根據現實意義使用其他列向量替代。

Softmax函數得到的是一個[0,1]之間的值，且∑Kk=1P(i)=1，這個softmax求出的概率就是真正的概率，換句話說，這個概率等於期望。

[Softmax 函數及其作用（含推導） ]

[Machine Learning - VI. Logistic Regression邏輯回歸 (Week 3) ]

模糊量化模式

新數據=1/2+1/2sin[派3.1415/（極大值-極小值）*（X-（極大值-極小值）/2） ] X為原數據

皮皮blog

數據標準化/歸一化的編程實現

Python庫實現和調用

[Scikit-learn：數據預處理Preprocessing data ]

from: http://blog.csdn.net/pipisorry/article/details/52247379

ref:

轉：數據標準化/歸一化normalization