PHP利用二叉堆實現TopK-算法的方法詳解
前言
在以往工作或者面試的時候常會碰到一個問題,如何實現海量TopN,就是在一個非常大的結果集裏面快速找到最大的前10或前100個數,同時要保證 內存和速度的效率,我們可能第一個想法就是利用排序,然後截取前10或前100,而排序對於量不是特別大的時候沒有任何問題,但只要量特別大是根本不可能 完成這個任務的,比如在一個數組或者文本文件裏有幾億個數,這樣是根本無法全部讀入內存的,所以利用排序解決這個問題並不是最好的,所以我們這裏就用 php去實現一個小頂堆來解決這個問題.
二叉堆
二叉堆是一種特殊的堆,二叉堆是完全二叉樹或者是近似完全二叉樹,二叉堆有兩種,最大堆 和 最小堆,最大堆:父結點的鍵值總是大於或等於任何一個子節點的鍵值;最小堆:父結點的鍵值總是小於或等於任何一個子節點的鍵值

小頂堆-(圖片來自網絡)
二叉堆一般用數組來表示(看上圖),例如,根節點在數組中的位置是0,第n個位置的子節點分別在2n+1和 2n+2,因此,第0個位置的子節點在1和2,1的子節點在3和4,以此類推,這種存儲方式便於尋找父節點和子節點。
具體概念問題這裏就不在多說了,如果對二叉堆有疑問的可以在好好了解下這個數據結構,下面我們就針對上述topN問題來用php代碼實現並解決,為了看出區別這裏先用排序的方式去實現下看下效果如何。
利用快速排序算法來實現 TopN
//為了測試運行內存調大一點 ini_set(‘memory_limit‘, ‘2024M‘); //實現一個快速排序函數 functionquick_sort(array $array){ $length = count($array); $left_array = array(); $right_array = array(); if($length <= 1){ return $array; } $key = $array[0]; for($i=1;$i<$length;$i++){ if($array[$i] > $key){ $right_array[] = $array[$i]; }else{ $left_array[] = $array[$i]; } }$left_array = quick_sort($left_array); $right_array = quick_sort($right_array); return array_merge($right_array,array($key),$left_array); } //構造500w不重復數 for($i=0;$i<5000000;$i++){ $numArr[] = $i; } //打亂它們 shuffle($numArr); //現在我們從裏面找到top10最大的數 var_dump(time()); print_r(array_slice(quick_sort($all),0,10)); var_dump(time());
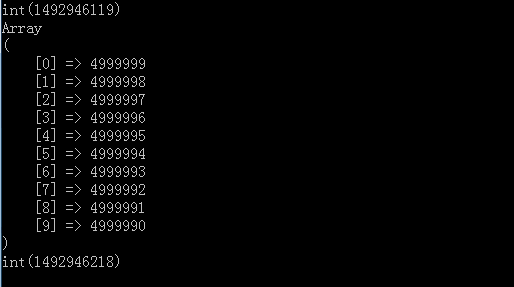
運行之後結果
可以看到上面打印出了top10的結果,並輸出了下運行時間,大概99s左右,但這只是500w個數且全部能裝入內存的情況,如果我們有一個文件裏面有5kw或5億個數,肯定就會有些問題了.
利用二叉堆算法來實現 TopN
實現流程是:
1、先讀取10個或100個數到數組裏面,這就是我們的topN數.
2、調用生成小頂堆函數,把這個數組生成一個小頂堆結構,這個時候堆頂一定是最小的.
3、從文件或者數組依次遍歷剩余的所有數.
4、每遍歷出來一個則跟堆頂的元素進行大小比較,如果小於堆頂元素則拋棄,如果大於堆頂元素則替換之.
5、跟堆頂元素替換完畢之後,在調用生成小頂堆函數繼續生成小頂堆,因為需要再找出來一個最小的.
6、重復以上4~5步驟,這樣當全部遍歷完畢之後,我們這個小頂堆裏面的就是最大的topN,因為我們的小頂堆永遠都是排除最小的留下最大的,而且這個調整小頂堆速度也很快,只是相對調整下,只要保證根節點小於左右節點就可以.
7、算法復雜度的話按top10最壞的情況下,就是每遍歷一個數,如果跟堆頂進行替換,需要調整10次的情況,也要比排序速度快,而且也不是把所有的內容全部讀入內存,可以理解成就是一次線性遍歷.
//生成小頂堆函數 function Heap(&$arr,$idx){ $left = ($idx << 1) + 1; $right = ($idx << 1) + 2; if (!$arr[$left]){ return; } if($arr[$right] && $arr[$right] < $arr[$left]){ $l = $right; }else{ $l = $left; } if ($arr[$idx] > $arr[$l]){ $tmp = $arr[$idx]; $arr[$idx] = $arr[$l]; $arr[$l] = $tmp; Heap($arr,$l); } } //這裏為了保證跟上面一致,也構造500w不重復數 /* 當然這個數據集並不一定全放在內存,也可以在 文件裏面,因為我們並不是全部加載到內存去進 行排序 */ for($i=0;$i<5000000;$i++){ $numArr[] = $i; } //打亂它們 shuffle($numArr); //先取出10個到數組 $topArr = array_slice($numArr,0,10); //獲取最後一個有子節點的索引位置 //因為在構造小頂堆的時候是從最後一個有左或右節點的位置 //開始從下往上不斷的進行移動構造(具體可看上面的圖去理解) $idx = floor(count($topArr) / 2) - 1; //生成小頂堆 for($i=$idx;$i>=0;$i--){ Heap($topArr,$i); } var_dump(time()); //這裏可以看到,就是開始遍歷剩下的所有元素 for($i = count($topArr); $i < count($numArr); $i++){ //每遍歷一個則跟堆頂元素進行比較大小 if ($numArr[$i] > $topArr[0]){ //如果大於堆頂元素則替換 $topArr[0] = $numArr[$i]; /* 重新調用生成小頂堆函數進行維護,只不過這次是從堆頂 的索引位置開始自上往下進行維護,因為我們只是把堆頂 的元素給替換掉了而其余的還是按照根節點小於左右節點 的順序擺放這也就是我們上面說的,只是相對調整下,並 不是全部調整一遍 */ Heap($topArr,0); } } var_dump(time());
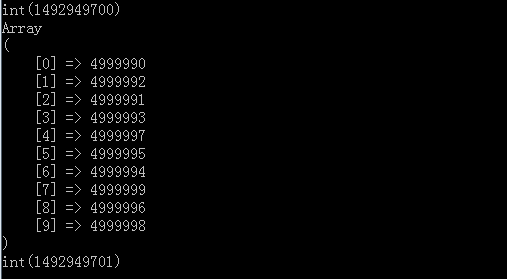
運行之後結果
可以看到最終的結果也是top10,只不過時間只用了1s左右,而且無論是內存還是時間效率都滿足我們的要求,而且跟排序比最好的一點就是不用把所 有的數據集都讀如到內存裏面來,因為我們不需要排序,而上面是為了演示,所以直接在內存構造了500w元素,然而我們可以把這個全部轉移到文件裏面去,然 後一行一行讀取進行比較,因為我們這個數據結構的核心點就是線性遍歷跟內存裏面很小的小頂堆結構進行比較,最終得到TopN.
總結
最後想說的就是 算法+數據結構 真的非常重要,一個好的算法可以使我們的效率大大提高。好了,以上就是這篇文章的全部內容了,希望本文的內容對大家的學習或者工作能帶來一定的幫助,如果有疑問大家可以留言交流,謝謝大家對腳本之家的支持。
原文鏈接:http://www.jianshu.com/p/df71c71cdc57
PHP利用二叉堆實現TopK-算法的方法詳解
