數據結構與算法-紅黑樹
前言
紅黑樹是工程中最常用到的一種自平衡二叉排序樹,其和AVL樹類似,都是在進行插入、刪除時通過一定的調整操作來維持相對穩定的樹高,從而獲得較好的查詢性能。
性質
1. 節點是紅色或黑色。
2. 根節點是黑色。
3 每個葉節點(null節點)是黑色的。
4 每個紅色節點的兩個子節點都是黑色。(從每個葉子到根的所有路徑上不能有兩個連續的紅色節點)
5. 從任一節點到其每個葉子的所有路徑都包含相同數目的黑色節點。
維護紅黑樹形狀(樹高)的,主要就是4、5兩條性質,性質4決定了最長的路徑莫過於紅黑間隔的路徑,性質5決定了最短的路徑莫過於全黑路徑,並且每條路徑上的黑色節點數都相同(相當關鍵),二者共同決定了最長路徑最多是最短路徑的2倍。
插入操作
插入的節點,應當是紅色的,因為在葉節點插入紅色節點不會違反性質5,而性質5恰恰是最難維護的。紅黑樹在插入操作後,需要維護性質2、4、5。
情況1:插入的是根節點。
原樹是空樹,此情況只會違反性質2,直接把此節點反轉為黑色即可。
情況2:插入的節點的父節點是黑色。
此不會違反性質2和性質4,紅黑樹沒有被破壞,什麽也不做。
情況3:插入節點的父節點是紅色且叔叔節點是紅色。
這種情況違反了性質4(新插入節點與父節點構成了連續的兩個紅節點),由於父節點與叔叔節點同為紅色,故可將二者同置為黑色(此時違反了性質5),並將祖父節點置為紅色(之前祖父節點一定為黑色)(遵守了性質5)。
N為插入節點
調整前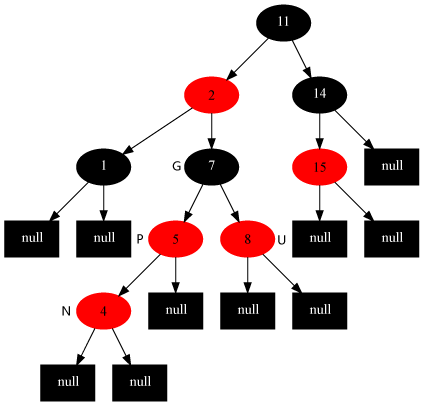
調整後
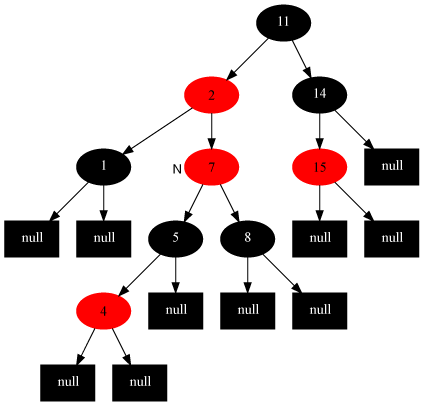
情況4:當前節點的父節點是紅色,叔叔節點是黑色,當前節點是其父節點的右子節點。
這種情況是最不好解決的,因為不管如何也無法通過一次變色或一次旋轉完成調整,這種情況通常會與情況5結合使用,首先以插入節點的父節點為軸左旋。
調整前
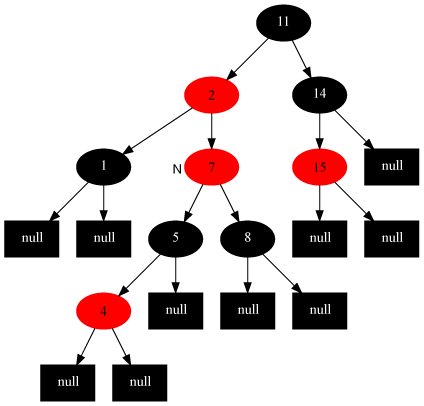
調整後
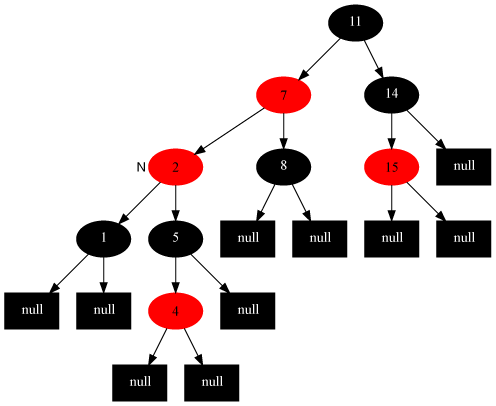
情況5:當前節點的父節點是紅色,叔叔節點是黑色,當前節點是其父節點的左子節點。
接情況4,將插入節點的父節點置黑、祖父節點置紅,以祖父節點為軸右旋。
調整前
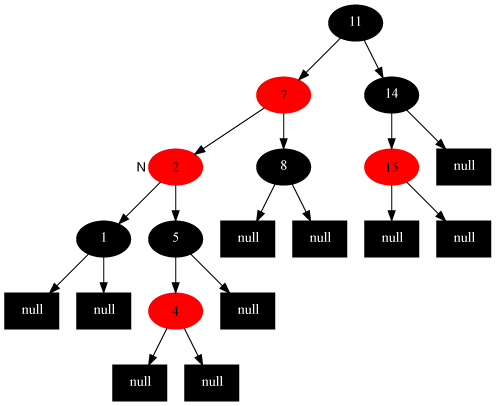
調整後
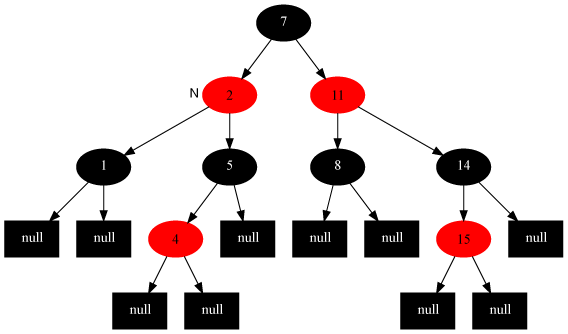
總結
紅黑樹並不追求“完全平衡”——它只要求達到一種相對平衡(而AVL對平衡的要求就很嚴格,為之做出的努力也越多),降低了對旋轉的要求,從而提高了性能。紅黑樹能夠以O(log2 n) 的時間復雜度進行搜索、插入、刪除操作。此外,由於它的設計,任何不平衡都會在三次旋轉之內解決
參考:http://www.imooc.com/article/11715
https://www.ibm.com/developerworks/cn/java/j-lo-tree/index.html
數據結構與算法-紅黑樹
