HDU1542-Atlantis【離散化&線段樹&掃描線】個人認為很全面的詳解
剛上大一的時候見過這種題,感覺好牛逼哇,這都能算
如今已經不打了,不過適當寫寫題保持思維活躍度還是不錯的,又碰到這種題了,想把它弄出來
說實話,智商不夠,看了很多解析,花了4、5個小時才弄明白
網上好多都是直說一半,弄得我很難受,需要查看很多題解不斷對比才清楚
首先線段樹這玩意,不光是線段樹吧,只要牽扯到遞歸都很抽象,要想好久
如果中途有哪些不懂,繼續看,代碼我盡量做到每一行都有註釋
1.離散化
先說離散化,這裏面牽扯到小數,而線段樹是維護一個整數區間,這是我們首先遇到的問題
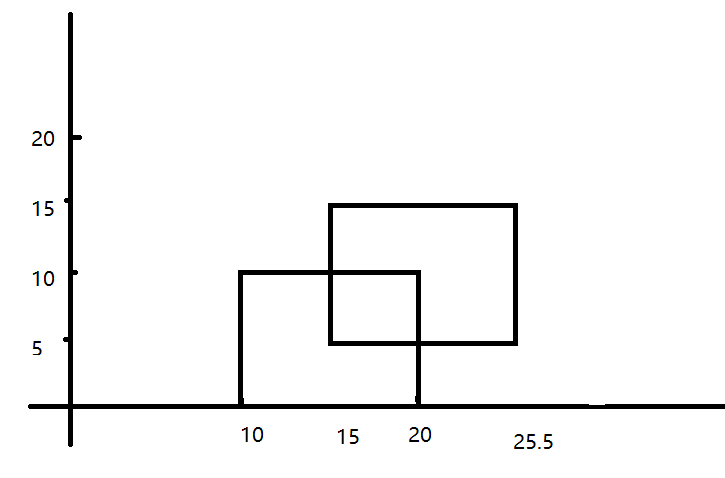
比如這種情況,第二個矩形剛好多了0.5怎麽辦哦
這時候就要用離散化來處理了,我個人感覺離散化說白了就是映射,先把一些難算的數值映射到一些簡單的數值上算完了再換回去
比如解物理題的時候先把一些不能拆開但很復雜的表達式用符號代替,算完了再換回去
那麽兩個矩形四條豎邊,對應的x分別是10、15、20、25.5,那麽久把這個不同的x值,存到數組裏dif_x[4] = {10,15,20,25.5}
用的時候,比如你要用到15~25.5這條邊的時候就用dif_x[3] - dif_x[1]得到10.5,就ok了
2.掃描線
你就想象有一根水平的線從下往上走,碰到邊就更新,這個有前人說的很詳細,我就直接拿來用了
http://www.cnblogs.com/Konjakmoyu/p/6050343.html
這個講的很好,我一開始理解掃描線就是看的這個
3.線段樹
首先你要有線段樹的基本知識嘛,這個就不說了
說一下裏面值的定義
struct node2 { int l,r,cnt; double len; }tree[1000];
這個也是這道題裏面最難理解的一部分
線段樹到底維護的什麽,或者說存放的什麽?
首先,根據掃描線的思路,你要存放的是當前掃描線的長度,這樣才能乘高度差
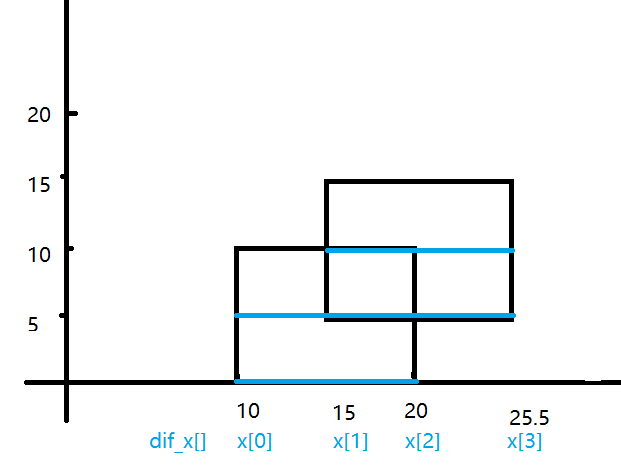
那麽你每次要更新的就是藍線的長度
那麽藍線的長度是不是可以由 dif_x[r] - dif_x[l]得到
比如我們第一次更新的這條藍線是10~20,那麽是不是可以由dif_x[] 數組的下標0~2來表示
第二次更新的藍線是10~25.5,是不是可以由0~3來表示
最後一次由1~3表示
那我們就知道了,線段樹裏的l,r其實存的是該結點所能涉及的dif_x[]數組的下標

結點1的l,r分別是0,3那麽就是10——25.5這條線段中,被覆蓋的長度
但是這裏就有一個問題了,0——1的長度可以理解,但是0是一個點,它的長度就是0啊
所以我麽規定,每一個坐標表示從它到它+1的點的長度
比如tree[4]表示,0~1的長度是5
tree[6]表示,2~3的長度是5.5
cnt表示該結點是否被覆蓋,參與這次面積的計算
double len 當然表示的就是該線段的長度了
補充
還需要一個比較重要的結構體
struct node { double x1,x2,y; int flag; void init(double l,double r,double h,int key) { x1 = l; x2 = r; y = h; flag = key; } }line[203];
這個結構體代表每一根橫線
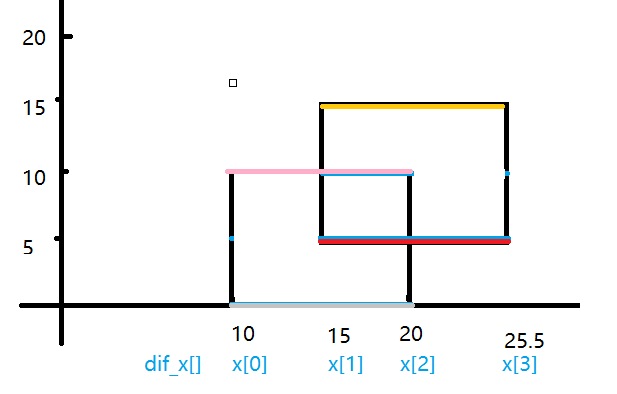
比如灰線代表line[0],紅線line[1],粉線line[2]以此類推
x1,x2就是這根線的左右端點坐標,y是這根線的y軸坐標,flag表示這根線是矩形的下面的線還是上面的線
這個很重要,如果是下面的線,在更新tree[]的時候,由於你是從下往上掃,所以要+1
如果是上面的線,在更新線段樹tree[]的時候,由於你是從下往上掃,所以要-1,表示你已經掃完了某個矩形,你要將矩形的上邊減掉
要講的就這麽多了吧
看代碼

1 #include<cstdio>
2 #include<cstring>
3 #include<algorithm>
4 using namespace std;
5
6 double dif_x[203];//記錄不同的x坐標
7
8 struct node
9 {
10 double x1,x2,y;
11 int flag;//各個參數上面說過
12 void init(double l,double r,double h,int key) {
13 x1 = l; x2 = r; y = h; flag = key;
14 }
15 }line[203];
16
17 bool cmp(node a, node b)
18 {
19 return a.y < b.y;
20 }
21
22 struct node2
23 {
24 int l,r,cnt;//各個參數上面說過
25 double len;
26 }tree[1000];
27
28 void build_tree(int id,int l,int r)//最基本的線段樹建樹不多說
29 {
30 tree[id].l = l;
31 tree[id].r = r;
32 tree[id].cnt = 0;
33 tree[id].len = 0;
34 if(l==r){
35 return;
36 }
37 int mid = (r + l)>>1;
38 build_tree(id<<1,l,mid);
39 build_tree((id<<1)+1,mid+1,r);
40 }
41
42 void getlen(int id)
43 {
44 if(tree[id].cnt >= 1) { //如果該段被覆蓋那麽就直接由dif_x數組獲得長度
45 tree[id].len = dif_x[tree[id].r+1] - dif_x[tree[id].l];//看了註釋①以後,應該不難理解了
46 }
47 else {
48 tree[id].len = tree[id<<1].len + tree[(id<<1)|1].len;//如果沒有被覆蓋,那麽應該是由左右孩子的和
49 }
50 }
51
52 void update(int id,int l,int r,int v)
53 {
54 if(tree[id].l==l && tree[id].r==r) {//目標區間
55 tree[id].cnt += v;//標記是否覆蓋
56 getlen(id);//算一下長度
57 return;
58 }
59 int mid = (tree[id].l+tree[id].r)>>1;
60 if(r <= mid){
61 update(id<<1,l,r,v);//更新左子樹
62 }
63 else if(l > mid) {
64 update((id<<1)+1,l,r,v);//更新右子樹
65 }
66 else {
67 update(id<<1,l,mid,v);
68 update((id<<1)+1,mid+1,r,v);//更新左右子樹
69 }
70 getlen(id);//push_up一下
71 }
72
73 int mySearch(double p, int l, int r)//二分找p在dif_x數組中的下標
74 {
75 while(l <= r)
76 {
77 int mid = (l + r)>>1;
78 if(dif_x[mid] == p){
79 return mid;//返回這個下標
80 }
81 if(dif_x[mid] < p) {
82 l = mid + 1;
83 }
84 else {
85 r = mid - 1;
86 }
87 }
88 }
89
90 int main()
91 {
92 int n,noc = 0;//number_of_case
93 while(~scanf("%d",&n))//輸入
94 {
95 if (n == 0) break;
96 noc ++;
97 double x1,y1,x2,y2;//矩形的位置參數
98 int line_num = 0;//一共有多少條橫線
99 for(int i=0;i<n;i++)//輸入
100 {
101 scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
102 line[line_num].init(x1,x2,y1,1);//下面的線,flag = 1
103 dif_x[line_num++] = x1;//數據中一共有多少個不同的橫坐標
104 line[line_num].init(x1,x2,y2,-1);//上面的線,flag = -1
105 dif_x[line_num++] = x2;
106 }
107 sort(line, line+line_num, cmp);//對橫線由低到高進行排序,因為你是從下往上掃描的
108 sort(dif_x, dif_x+line_num);//對dif_x去重,要先排個序,這樣更方便
109 int dif_x_num = unique(dif_x, dif_x+line_num) - dif_x;//dif_x_num表示去重後不同的x坐標的數量
110 build_tree(1,0,dif_x_num-1);//建立線段樹
111 double ans = 0;//最終的答案
112 for(int i=0;i<line_num-1;i++)//開始掃描
113 {
114 int line_l = mySearch(line[i].x1,0,dif_x_num-1);//第i根線的左端點對應在dif_x的下標
115 int line_r = mySearch(line[i].x2,0,dif_x_num-1)-1;//右邊要減一,看註釋①
116 update(1,line_l,line_r,line[i].flag);//更新線段樹
117 ans += tree[1].len * (line[i+1].y - line[i].y);//求面積,tree[1]就是總長度嘛
118 }
119 printf("Test case #%d\n",noc);
120 printf("Total explored area: %.2lf\n\n",ans);
121 }
122 }
註釋① 這裏我看了n多題解,沒一個說為什麽-1,管這個我就懵逼了70%的時間,希望看了這個會節約你很多時間
其實我前面已經說了,每個點代表從它到它+1的點的長度,那麽你要求0~3的長度,其實要求的是0~2的長度
好辛苦,終於寫完了,希望對你有幫助!
HDU1542-Atlantis【離散化&線段樹&掃描線】個人認為很全面的詳解
