鄰接列表及其類似結構

　　對於圖結構的實現來說，最直觀的方式之一就是使用鄰接列表。下面我們來實現一個最簡單的：假設現在我們有n個節點，編號分別為0，...，n-1。

　　然後，每個鄰接列表就是一個數字列表，我們可以將他們編入一個大小為n的主列表，並用節點編號對其進行索引。

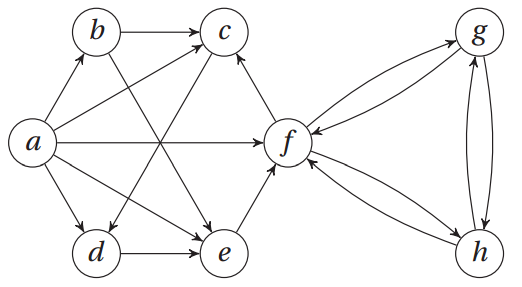
　　鄰接集表示法：

a, b, c, d, e, f, g, h = range(8)
N = [
 {b, c, d, e, f},        # a
 {c, e},                 # b
 {d},                    # c
 {e},                    # d
 {f},                    # e
 {c, g, h},              # f
 {f, h},                 # g
 {f, g}                  # h
] 

　　鄰接列表

a, b, c, d, e, f, g, h = range(8)
N = [
 [b, c, d, e, f],        # a
 [c, e],                 # b
 [d],                    # c
 [e],                    # d
 [f],                    # e
 [c, g, h],              # f
 [f, h],                 # g
 [f, g]                  # h
] 

　　加權鄰接字典

a, b, c, d, e, f, g, h = range(8)
N = [
 {b:2, c:1, d:3, e:9, f:4},   # a
 {c:4, e:3},                  # b
 {d:8},                       # c
 {e:7},                       # d
 {f:5},                       # e
 {c:2, g:2, h:2},             # f
 {f:1, h:6},                  # g
 {f:9, g:8}                   # h
]

鄰接矩陣

　　嵌套 list 實現的鄰接矩陣

a, b, c, d, e, f, g, h = range(8)
# a b c d e f g h
N = [[0,1,1,1,1,1,0,0], # a
     [0,0,1,0,1,0,0,0], # b
     [0,0,0,1,0,0,0,0], # c
     [0,0,0,0,1,0,0,0], # d
     [0,0,0,0,0,1,0,0], # e
     [0,0,1,0,0,0,1,1], # f
     [0,0,0,0,0,1,0,1], # g
     [0,0,0,0,0,1,1,0]] # h 

　　由於圖上沒有自循環狀態，其對角線上的值應該全為假。

　　無向圖的鄰接矩陣應該是一個對稱矩陣。

　　我們通常會把不存在的邊的權值設置為無窮大。

inf = float(‘inf‘)
a, b, c, d, e, f, g, h = range(8)
# a b c d e f g h
N = [[inf, 1 , 1 , 1 , 1 , 1 ,inf,inf], # a
     [inf,inf, 1 ,inf, 1 ,inf,inf,inf], # b
     [inf,inf,inf, 1 ,inf,inf,inf,inf], # c
     [inf,inf,inf,inf, 1 ,inf,inf,inf], # d
     [inf,inf,inf,inf,inf, 1 ,inf,inf], # e
     [inf,inf, 1 ,inf,inf,inf, 1 , 1 ], # f
     [inf,inf,inf,inf,inf, 1 ,inf, 1 ], # g
     [inf,inf,inf,inf,inf, 1 , 1 ,inf]] # h 

　　在鄰接矩陣中，查詢變（u,v）需要的時間為Θ（1），遍歷v鄰居的操作時間為Θ（n）；

　　鄰接列表中，兩種操作所需的時間都為Θ（d（v））

　　我們應該根據圖的具體用處來選擇相關的表示法。

樹的實現

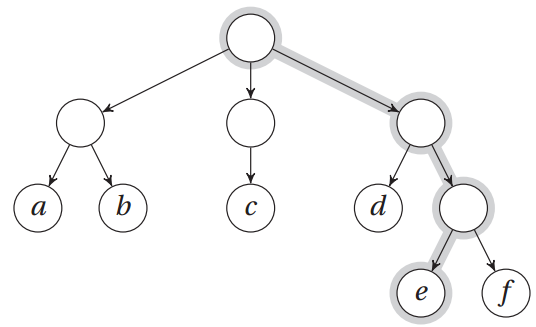
　　樹表示成一個二維列表

>>> T = [["a", "b"], ["c"], ["d", ["e", "f"]]]
>>> T[0][1]
‘b‘
>>> T[2][1][0]
‘e‘ 

　　二叉樹類：

class Tree:
　　def __init__(self, left, right):
　　self.left = left
　　self.right = right

>>> t = Tree(Tree("a", "b"), Tree("c", "d"))
>>> t.right.left
‘c‘ 

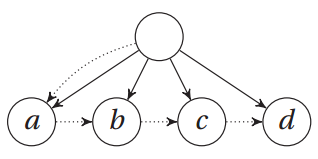
　　多路搜索樹類：

class Tree:
    def __init__(self, kids, next=None):
    self.kids = self.val = kids
    self.next = next
    
>>> t = Tree(Tree("a", Tree("b", Tree("c", Tree("d")))))
>>> t.kids.next.next.val
‘c‘

　　Bunch模式：

class Bunch(dict):
    def __init__(self, *args, **kwds):
    super(Bunch, self).__init__(*args, **kwds)
    self.__dict__ = self

>>> T = Bunch
>>> t = T(left=T(left="a", right="b"), right=T(left="c"))
>>> t.left
{‘right‘: ‘b‘, ‘left‘: ‘a‘}
>>> t.left.right
‘b‘
>>> t[‘left‘][‘right‘]
‘b‘
>>> "left" in t.right
True
>>> "right" in t.right
False 

【Python算法】圖與樹的實現