HDU 6073 Matching In Multiplication(拓撲排序)
阿新 • • 發佈:2017-08-05
str graph pop using bsp sum rod 沒有 script
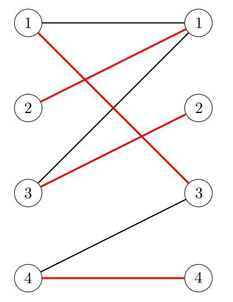
Little Q misunderstands the definition of bipartite graph, he thinks the size of U is equal to the size of V, and for each vertex p in U, there are exactly two edges from p. Based on such weighted graph, he defines the weight of a perfect matching as the product of all the edges‘ weight, and the weight of a graph is the sum of all the perfect matchings‘ weight.
In each test case, there is an integer n(1≤n≤300000) in the first line, denoting the size of U. The vertex in U and V are labeled by 1,2,...,n.
For the next n lines, each line contains 4 integers vi,1,wi,1,vi,2,wi,2(1≤vi,j≤n,1≤wi,j≤109), denoting there is an edge between Ui and Vvi,1, weighted wi,1, and there is another edge between Ui and Vvi,2, weighted wi,2.
It is guaranteed that each graph has at least one perfect matchings, and there are at most one edge between every pair of vertex. Output For each test case, print a single line containing an integer, denoting the weight of the given graph. Since the answer may be very large, please print the answer modulo 998244353. Sample Input 1 2 2 1 1 4 1 4 2 3 Sample Output 16 【題意】給你一個二分圖,每一集合裏的 點數量 都為n,且其中一個集合裏每個點的度數都為2.然後對於每一種完美匹配,算出邊權值的乘積,然後再將每一種匹配的乘積加起來,輸出最後結果。 【分析】U集合裏的點 度數都為二,V集合裏的點度數未知,但加起來肯定為2*n,對於V集合裏度數為1的點,它的匹配對象是固定的,所以我們用拓撲排序將度數為1的點全部挖出,算出乘積res。然後對於剩下 的圖,假設總節點為2*m,則V集合總度數為2*m,由於此時V集合裏已經,沒有度數為1的點,所以V集合裏點的度數都為2,這說明這個圖每個連通塊是個環,在環上間隔著取即可,一共兩種方案。比如對於兩個聯通塊,他倆的兩種方案乘積分別是(a1,a2),(b1,b2),則答案為a1*b1+a1*b2+a2*b1+a2*b2,化簡後為(a1+a2)*(b1+b2),最後在乘以res即可。
Matching In Multiplication
Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)
Total Submission(s): 1127 Accepted Submission(s): 325

Little Q misunderstands the definition of bipartite graph, he thinks the size of U is equal to the size of V, and for each vertex p in U, there are exactly two edges from p. Based on such weighted graph, he defines the weight of a perfect matching as the product of all the edges‘ weight, and the weight of a graph is the sum of all the perfect matchings‘ weight.
In each test case, there is an integer n(1≤n≤300000) in the first line, denoting the size of U. The vertex in U and V are labeled by 1,2,...,n.
For the next n lines, each line contains 4 integers vi,1,wi,1,vi,2,wi,2(1≤vi,j≤n,1≤wi,j≤109), denoting there is an edge between Ui and Vvi,1, weighted wi,1, and there is another edge between Ui and Vvi,2, weighted wi,2.
It is guaranteed that each graph has at least one perfect matchings, and there are at most one edge between every pair of vertex. Output For each test case, print a single line containing an integer, denoting the weight of the given graph. Since the answer may be very large, please print the answer modulo 998244353. Sample Input 1 2 2 1 1 4 1 4 2 3 Sample Output 16 【題意】給你一個二分圖,每一集合裏的 點數量 都為n,且其中一個集合裏每個點的度數都為2.然後對於每一種完美匹配,算出邊權值的乘積,然後再將每一種匹配的乘積加起來,輸出最後結果。 【分析】U集合裏的點 度數都為二,V集合裏的點度數未知,但加起來肯定為2*n,對於V集合裏度數為1的點,它的匹配對象是固定的,所以我們用拓撲排序將度數為1的點全部挖出,算出乘積res。然後對於剩下 的圖,假設總節點為2*m,則V集合總度數為2*m,由於此時V集合裏已經,沒有度數為1的點,所以V集合裏點的度數都為2,這說明這個圖每個連通塊是個環,在環上間隔著取即可,一共兩種方案。比如對於兩個聯通塊,他倆的兩種方案乘積分別是(a1,a2),(b1,b2),則答案為a1*b1+a1*b2+a2*b1+a2*b2,化簡後為(a1+a2)*(b1+b2),最後在乘以res即可。
#include <bits/stdc++.h> #define inf 0x3f3f3f3f #define met(a,b) memset(a,b,sizeof a) #define pb push_back #define mp make_pair #define inf 0x3f3f3f3f #define qwer 2e18 using namespace std; typedef long long ll; const int N = 6e5+50; const int M = 16000009; const int mod = 998244353; const double pi= acos(-1.0); typedef pair<int,int>pii; int n,s; int vis[N],in[N]; ll ans[2]; vector<pii>edg[N]; ll topSort(){ queue<int>q; ll ret=1; for(int i=n+1;i<=n+n;i++){ if(in[i]==1){ q.push(i); vis[i]=1; } } while(!q.empty()){ int u=q.front(); q.pop(); for(int i=0;i<edg[u].size();i++){ int v=edg[u][i].first; if(vis[v])continue; if((--in[v])==1)q.push(v),vis[v]=1; if(u>n)ret=(ret*1LL*edg[u][i].second)%mod; } } return ret; } void dfs(int u,int ty,int fa){ vis[u]=1; for(int i=0;i<edg[u].size();i++){ int v=edg[u][i].first; if(v==s&&v!=fa)ans[ty]=(ans[ty]*1LL*edg[u][i].second)%mod; if(vis[v])continue; ans[ty]=(ans[ty]*1LL*edg[u][i].second)%mod; dfs(v,ty^1,u); } } int main(){ //freopen("de.txt","r",stdin); int T; scanf("%d",&T); while(T--){ scanf("%d",&n); for(int i=0;i<N;i++)vis[i]=in[i]=0,edg[i].clear(); for(int i=1,v1,w1,v2,w2;i<=n;i++){ scanf("%d%d%d%d",&v1,&w1,&v2,&w2); v1+=n;v2+=n; edg[i].pb(mp(v1,w1)); edg[v1].pb(mp(i,w1)); edg[i].pb(mp(v2,w2)); edg[v2].pb(mp(i,w2)); in[i]+=2; in[v1]++;in[v2]++; } ll anss=topSort(); for(s=1;s<=n;s++){ if(!vis[s]){ ans[0]=ans[1]=1; dfs(s,0,0); anss=anss*((ans[0]+ans[1])%mod)%mod; } } printf("%lld\n",anss); } return 0; }
HDU 6073 Matching In Multiplication(拓撲排序)
