【基礎知識三】線性模型
一、基本形式
通過屬性的線性組合來進行預測,
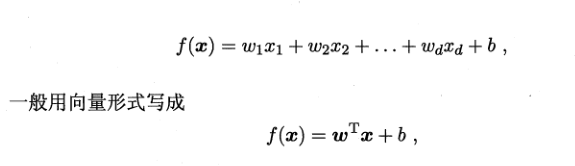
許多非線性模型可以在線性模型的基礎上,引入層級結構或高維映射而得。
二、線性回歸
最小二乘法:求解ω和b;
多元線性回歸:樣本由多個屬性描述,即x為多維向量;
若矩陣不滿秩產生多個解,解決方法:引入正則化項;
三、對數/邏輯線性回歸
廣義線性模型:

g(.)條件:連續且充分光滑(單調可微)
為了預測值連續,引入Sigmoid函數
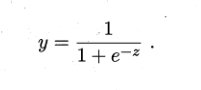
得到,
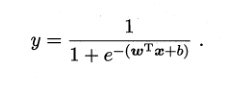
極大似然估計:求解ω和b
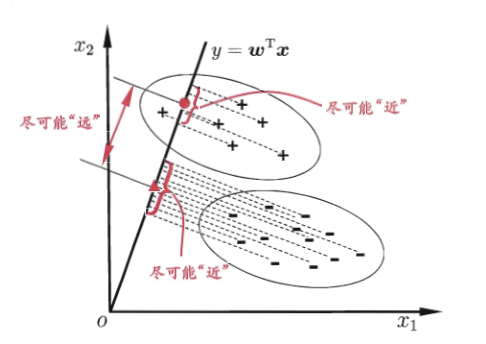
四、線性判別分析LDA
也叫“Fisher判別”
將樣例投影到一條直線上,使同類樣例投影點盡可能接近,異類樣例投影點盡可能遠離;
五、多分類策略
“一對一”
“一對其余” one vs rest/ one vs all
“多對多”
六、類別不平衡問題
假設 正例<反例
“再平衡”“再縮放”:根據正、反例比例調節閾值
對反例“欠采樣”
對正例“過采樣”
註意:這裏“欠采樣”與“過采樣”均有專門算法,不能簡單“隨機丟棄”或者“隨機重復”。
【基礎知識三】線性模型
相關推薦
【基礎知識三】線性模型
解決方法 最小 方法 不能 其余 比例 http 正則 註意 一、基本形式 通過屬性的線性組合來進行預測, 許多非線性模型可以在線性模型的基礎上,引入層級結構或高維映射而得。 二、線性回歸 最小二乘法:求解ω和b; 多元線性回歸:樣本由多個屬性描述,即x為多維向量; 若矩
【基礎知識八】集成學習
大致 p s 學習方法 ron 完成 ima 結合 alt http 難點:如何產生“好而不同”的個體學習器;“好而不同”:“準確性”和“多樣性” 一、個體與集成 構建並結合多個學習器來完成學習任務 集成:結果通過投票法voting產生,“少數服從多數” 獲得整體性能提升要
【軟考】——軟體工程基礎知識(軟體過程模型)
軟體過程模型 軟體過程模型???——》 軟體過程模型???——》瀑布模型、增量模型、演化模型、噴泉模型、基於構建的開發模型、形式化方法模型、統一過程模型、敏捷方法; 瀑布模型???——》以
【基礎知識】ActiveMQ基本原理
system 鏈接 以及 重啟 alt 過濾器 全部 pro 相關 “來,根據你的了解說下 ActiveMQ 是什麽。” “這個簡單,ActiveMQ 是一個 MOM,具體來說是一個實現了 JMS 規範的系統間遠程通信的消息代理。它&h
【基礎知識十六】強化學習
動態 sof col -s 範例 如何 差分 ash 抽象 一、任務與獎賞 我們執行某個操作a時,僅能得到一個當前的反饋r(可以假設服從某種分布),這個過程抽象出來就是“強化學習”。 強化學習任務通常用馬爾可夫決策過程MDP來描述: 強化學
Unity學習(三)Unity Shader入門(基礎知識篇)+線性代數複習(未完待續)
至於為什麼剛建立了指令碼,現在就要做Shader了。。說多了都是淚 1.建立一個新的材質 Material Assert -> Create -> Material 拖到Scene中的某個物體上 2.建立一個新的Shader Assert -> Create -
【 MAKEFILE 程式設計基礎之三】詳解 MAKEFILE 變數的定義規則使用!
本站文章均為 李華明Himi 原創,轉載務必在明顯處註明: 轉載自【黑米GameDev街區】 原文連結: http://www.himigame.com/gcc-makefile/770.html 使用變數: 在Mak
【問鏈-區塊鏈基礎知識系列】 第十課 首席架構師談區塊鏈技術演進
一、區塊鏈和比特幣,都有“幣-鏈-網”三層含義 1、第一層含義是“幣”。這個“幣”並不是剛才王行長所說的真正意義上的“貨幣”,而是一種與區塊鏈密切相關的通證(Blockchain Token)。其本質,是記錄在區塊鏈賬本結構中的某個“元資訊”。例如,比特幣區塊鏈的賬本中的記錄的主要元資料
【問鏈財經-區塊鏈基礎知識系列】 第十六課 區塊鏈將變革教育產業,未來有六大應用方向
區塊鏈是什麼? 2008 年中本聰發表的論文《比特幣:一種點對點的電子現金系統》。文章提出,希望可以建立一套新型的電子支付系統,這套系統“基於密碼學原理而不是基於信用,使得任何達成一致的雙方能夠直接進行支付,從而不需要第三方中介參與”。 2009 年 1 月 3 日,區塊鏈的第一個區
【JAVA基礎知識學習】Java中的String,StringBuilder,StringBuffer三者的區別
最近在學習Java的時候,遇到了這樣一個問題,就是String,StringBuilder以及StringBuffer這三個類之間有什麼區別呢,自己從網上搜索了一些資料,有所瞭解了之後在這裡整理一下,便於大家觀看,也便於加深自己學習過程中對這些知識點的記憶,如果哪
【問鏈財經-區塊鏈基礎知識系列】 第十七課 區塊鏈應用於汽車保險行業所帶來的變革
編者按:在一般汽車保險詐騙案,汽車駕駛會故意安排假車禍,然後向保險公司提出各種不實和非法的索賠。據德勤(Deloitte)統計,這些假車禍每年讓保險業損失約7億新元。汽車駕駛若對不同保險公司索賠,除非共享跨產業資料,否則很難發現欺詐行為。區塊鏈結合汽車保險行業將會產生新的火花。
【數字訊號處理】線性卷積的三種常見求解方法
例:x(n)=R3(n)={1,1,1};h(n)=(4-n)R4(n)={4,3,2,1};求線性卷積y(n)=x(n)*h(n) 1、時域直接法: a.翻轉:h(n)=h(-m); b.移位:h(n-m); c.相乘:x(m)h(n-m); d.相加
【問鏈財經-區塊鏈基礎知識系列】 第十八課 區塊鏈應用於貸款結算
編者按:在金融業務中,企業或個人向金融機構進行借貸,產生貸款業務,貸款結算是當貸款所有本金、利息和費用都收回後,貸款即告結清。貸款結清是信貸資金的風險已不存在,貸款安全回收,併為銀行帶來了收益。那結合區塊鏈,貸款結算會帶來哪些改變? 商業銀行的主要業務有三類:其一,存款
【問鏈財經-區塊鏈基礎知識系列】 第十九課 區塊鏈應用於電子存證
編者按:在傳統的具有法律效益的存證需要第三方權威公證處進行公證,並且需要繫結時間戳和相關資訊,步驟繁瑣,進度比較慢,後來存證電子化後一定程度上提高了效率、節省了成本,但也會有一些其他的問題,比如第三方篡改電子存證,雖然絕大多數這種情況不會發生,但是當涉及到巨大的利益時,就很難保證
【基礎知識】:比特幣原理解析
一、比特幣的背景 對於當下流行的電子貨幣-比特幣系統,朋友圈裡有很多介紹性的文章,也有人試圖通過漫畫來生動的解釋比特幣的特性,但是始終不得要領,總是有些問題想不清楚,為了弄清楚這些問題,最近深入的研讀了幾本比特幣的書籍以及中本聰本人發表的比特幣論文,感覺茅塞頓開,迫不及待的與大家分享我的理解,希望與大家
【問鏈財經-區塊鏈基礎知識系列】 第二十課 區塊鏈聯盟鏈攻伐戰
編者按:聯盟鏈是目前區塊鏈落地實踐的熱點,也是大家對“殺手級應用”期望最大的區塊鏈部署形態。聯盟鏈的誕生源於對區塊鏈技術的“反思”,是對比特幣、以太坊所體現的技術特點與企業客戶實際需要的融合與折衷,蘊含了大量區塊鏈工作者的智慧與辛勞。 由於對未來價值的“共識”,很多廠商推出了自
【redis 基礎篇三】set集合常用命令
在使用集合的過程中,我們都明白他是通過Key-value的形式來儲存的,在存入資料的時候將值賦值給一個key值,去出的時候,我不管你那個value值跑到了什麼位置,我只要通過這個key值就可
【基礎知識思考整理 】Mysql高效率的分頁查詢
在工程實踐中,資料庫表中的資料量一般不超過 100W行。當我們想要查詢資料表中滿足條件的第 n個100 行資料的時候,怎樣的查詢方法才能保證較高的效能呢? 首先想到的,一般分頁都是用 “limit 起始, 行數” 這樣的方式。 上面的含義是:即使我們
【基礎知識思考整理 】Zero-copy原理理解(使用者角度)
關於Zero-Copy的原理。主要參照的是一篇03年的文章[1](Linux Journal),原理講得很明白。 首先需要知道應用場景: 適用於靜態資源從磁碟到網路的傳送(中間不對資源進行改變),這在web server提供的功能中很常見,一個例子是:
【Java核心知識三】抽象類和介面
介面和內部類為我們提供了一種將介面和實現分離的更加結構化的方法 抽象類和抽象方法 抽象方法:不完整,僅有申明而沒有方法體。 abstract void f(); 抽象類: 包
