8.11聯考題解

樣例輸入:
3 6
0 -1 1
1 0 -1
-1 1 0
1 2 3 1 2 3
樣例輸出:
3

題解
不要看上面那個嚇人的時間限制……實際上內網給了4Sec,高明的模擬能過;外網給的時間比這還多,直接暴力模擬就能A,這就是為什麽我今天成績莫名高了不少。剛開始就只想到了模擬,用鏈表可以稍微優化一點有限,然而時間效率近似於n*答案,要依靠答案的大小來決定時間效率,讓我不由得想到某名為《天鵝會面》的慘痛事故。想了很久還是沒想出來,直接把模擬當做騙分程序來寫,連快讀都沒有寫;自認為是今天最不靠譜的一個程序。曾經想過每次至少有一個鐘會破產,可以依據這個優化一下,但是當時沒有想到應該怎麽維護財產,覺得優化之後反而不準確就幹脆沒有改。競賽到時間之後一刷新……誒……這道題居然A了?!我打的不是暴力無剪枝模擬嗎?然後第一次覺得外網評測機好像跑得還不算太慢。交到內網按測試點計時,最後一個點過不了。ryf大佬的方法在普通模擬的基礎上每次把一個鐘破產的最早時間作為單位時間,節省了很多冗余的步驟,速度快到飛起,優化之後在內網也輕松過掉。題解上提到可以證明至多在3*n秒內會終止,這大約也是模擬可行的重要依據。然而應該怎樣證明呢?並不是很清楚,在考場上做一個這種級別的證明大概也是不值得的吧。

#include<iostream> #include<cstdio> #include<cstring> using namespace std; const int sj=1000005; int c,n,cl[sj],ft[105][105],cc[sj],cz[105],zls; int pr[sj],nt[sj],zq,ss[sj]; bool wd; inline int r(){ int s=0,k=1;char ch=getchar(); while(ch<48||ch>‘9‘) k=(ch==‘-‘)?-1:k,ch=getchar();clockwhile(ch>47&&ch<=‘9‘)s=s*10+(48^ch),ch=getchar(); return s*k; } void bj(int &x,int y) { x=x<y?x:y; } int main() { c=r(); n=r(); for(int i=1;i<=c;i++) { wd=1; for(int j=1;j<=c;j++) { scanf("%d",&ft[i][j]); if(ft[i][j]<0) wd=0; } if(wd) { printf("%d",i); return 0; } } for(int i=1;i<=n;i++) { cl[i]=r(),cc[i]=1; pr[i]=i-1,nt[i]=i+1; if(cz[cl[i]]==0) zls++; cz[cl[i]]++; } nt[0]=1,nt[n]=0; while(zls!=1) { zq=0x7fffffff; for(int i=nt[0];i;i=nt[i]) { ss[i]=0; if(pr[i]) ss[i]+=ft[cl[i]][cl[pr[i]]]; if(nt[i]) ss[i]+=ft[cl[i]][cl[nt[i]]]; if(ss[i]<0) bj(zq,(cc[i]-1)/(-ss[i])+1); } for(int i=nt[0];i;i=nt[i]) cc[i]+=zq*ss[i]; for(int i=nt[0];i;i=nt[i]) if(cc[i]<=0) { cz[cl[i]]--; if(cz[cl[i]]==0) zls--; pr[nt[i]]=pr[i]; nt[pr[i]]=nt[i]; } } for(int i=0;i!=n+1;i=nt[i]) if(i!=0) { printf("%d",cl[i]); break; } return 0; }

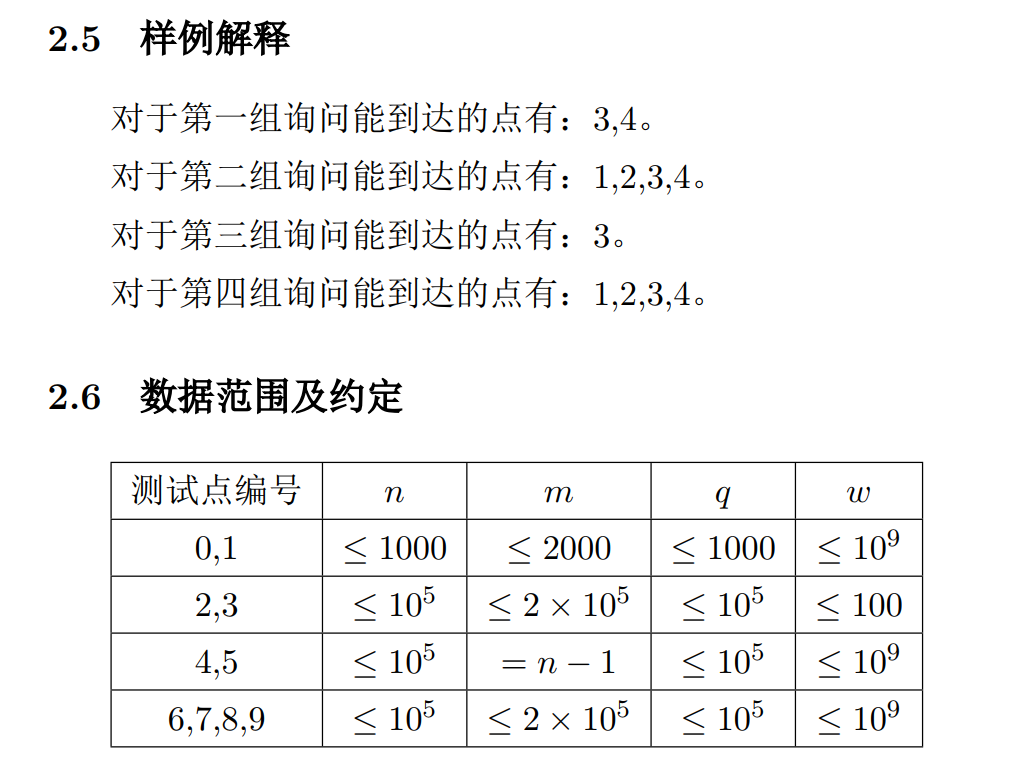
2.4 樣例輸入輸出
樣例輸入:
4 4 4
1 2 1
2 3 3
3 4 2
4 1 4
3 2
3 3
3 1
3 4
樣例輸出:
2
4
1
4
題解
題幹很簡單,但是解決也不是那麽容易。剛開始非常直接地打了個dfs暴力查詢,大概只能拿20分。受到測試點的啟發,樹是比較容易的圖形,然後想到了最小生成樹。圖不算特別稠密,不是必須要用普裏姆,不花什麽力氣就打出了克魯斯卡爾。然而這樣只不過是把一次dfs的復雜度上限從2*m降到了n,並沒有優化太多,想要拿比20更多的分還是很沒底。如果預處理到每點的最大邊權,時間和空間復雜度都承受不了。從圖到樹,難道還要從樹到鏈嗎?但是想了想樹鏈剖分感覺並不靠譜。到最後都沒有想出正解,交上了20分的程序。
正解是在克魯斯卡爾過程中維護並查集(或者用一些叫做克魯斯卡爾重構樹的神奇東西?)。雖然圖上的邊和詢問看起來完全不是一種東西,它們卻都有對邊權的要求。曾經想過對每一個詢問中的w生成一棵樹,然而問題在於時間復雜度太高也未必真能生成一棵完整的樹。但是如果把詢問像圖上的邊一樣記錄下來,在克魯斯卡爾給邊排序時一同排序,就可以在生成樹的過程中機智無比地解決問題了。克魯斯卡爾對於樹的鑒定是通過並查集實現的,我們在這裏也用並查集,甚至不用真正構建生成樹,只要把集合大小作為附加信息維護就可以了,集合的大小正是把當前邊權作為最大邊權所能到達的點數。唯一的一點細節是當邊權與詢問的w相同時先加邊再詢問。正所謂四兩撥千斤,喜歡並查集的最主要原因 就是它能用非常巧妙的方法解決看似復雜的問題,思維轉化的過程又妙趣橫生,維護附加信息的操作更是讓人拍案叫絕。如果下次我能用並查集A一道題,一定會非常高興的。

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int sj=100005; int n,m,q,a1,a2,a3,e2,l[sj],fa[sj],size[sj],ans[sj]; struct yb { int ne,w,v,u,lx; }c[sj*6]; void ad2(int x,int y,int z,int op) { c[e2].v=y; c[e2].u=x; c[e2].w=z; c[e2].lx=op; c[e2].ne=l[x]; l[x]=e2++; } int comp(const yb&a,const yb&b) { return (a.w==b.w)?(a.lx>b.lx):(a.w<b.w); } int find(int x) { if(fa[x]==x) return x; fa[x]=find(fa[x]); return fa[x]; } void hb(int x,int y) { x=find(x),y=find(y); if(x!=y) fa[x]=y; size[y]+=size[x]; } int main() { scanf("%d%d%d",&n,&m,&q); memset(l,-1,sizeof(l)); for(int i=1;i<=m;i++) { scanf("%d%d%d",&a1,&a2,&a3); ad2(a1,a2,a3,1); ad2(a2,a1,a3,1); } for(int i=1;i<=n;i++) fa[i]=i,size[i]=1; for(int i=1;i<=q;i++) { scanf("%d%d",&a1,&a2); ad2(a1,i,a2,0); } sort(c+0,c+e2,comp); for(int i=0;i<e2;i++) { if(c[i].lx==1) if(find(c[i].v)!=find(c[i].u)) hb(c[i].u,c[i].v); if(c[i].lx==0) ans[c[i].v]=size[find(c[i].u)]; } for(int i=1;i<=q;i++) printf("%d\n",ans[i]); return 0; }travel
區間第K大(kth)
出題人:任路遙
時間限制:2s 空間限制:256MB
【題目描述】
想必大家對區間第K大問題相當熟悉了。這個問題是這樣的,給一串序列和若幹詢問,每個詢問查詢某段連續區間中第K大的數。現在我們考慮一個該問題的“Reverse”版本。現在我們給出序列和Q個詢問,每個詢問給出K_i和X_i,詢問有多少區間其第K_i大的數為X_i。
【輸入說明】
第一行一個整數N和Q,表示序列長度和詢問個數。
第二行N個整數A_i,表示序列中的元素。
接下來Q行,每行兩個整數K_i和X_i,表示詢問。
【輸出說明】
一共Q行,每行表示對應詢問的答案。
【樣例輸入】
3 2
1 1 2
1 1
2 1
【樣例輸出】
3
3
【數據範圍】
對於20%的數據,N<=100
對於40%的數據,N<=500
對於100%的數據,N<=2000,Q<=2000000, 1 ≤ K_i ≤ N,1 ≤ X_i ≤ N
【題解】
剛開始的時候打算先打個不管不顧的暴力,什麽時間復雜度都行。後來看了看詢問數2*10^6,而且還不分層,在它的基礎上乘上什麽都很難不超時啊,所以說這題離線或者預處理算是穩了吧。預處理比較好打,畢竟n和k的範圍都只有2000,直接n^3枚舉和遍歷區間,加上每次快排的logn,40分拿得還是比較穩。然而用這種思路來做實在是沒有優化空間,區間枚舉少一點答案就會不準確,果然正解用的是一種截然不同的思路。
回憶一下前天T1calc,那道順序對的題,一個數對答案的貢獻取決於前後和它有某種特殊關系的數的數量。這道題也是一樣,一個數在區間裏第k大不就是說明有k-1個數比它更大嗎?對於每一個數枚舉它左右比它大的所有數的位置,只要在一個比它大的數一側,又沒有到下一個數,這一段裏的點都可以作區間的一個端點。根據乘法計數原理,兩邊可行的端點數相乘就是可行答案數。左邊取到的數越來越少,就要求右邊取到的越來越多,只要滿足左+右=k-1即可。對於序列中的每一個數枚舉它所在區間的的左側端點右側端點,不到n^3的效率就能得出所有答案,最後o(1)查詢。計算左邊的時候等號可取,右邊則不取,可以有效地避免重復計數。
正解確實很巧妙,可是畢竟做過calc,本該想到的。一個類型的題總是要多做幾遍才能形成思路,然而最有效的方法大概是考試丟分吧(笑),自從那次考試前綴和沒想到丟了幾十分之後做題再也不會完全想不起前綴和了~

#include<iostream> #include<cstdio> #include<cstring> using namespace std; const int sj=2005; int f[sj][sj],a[sj],n,a1,a2,q[sj],h[sj],qi; int main() { scanf("%d%d",&n,&qi); for(int i=1;i<=n;i++) scanf("%d",&a[i]); for(int i=1;i<=n;i++) { a1=a2=0; for(int j=i-1;j>0;j--) if(a[i]<=a[j]) q[++a1]=j; q[a1+1]=0; for(int j=i+1;j<=n;j++) if(a[j]>a[i]) h[++a2]=j; h[a2+1]=n+1; q[0]=h[0]=i; for(int j=0;j<=a1;j++) for(int k=0;k<=a2;k++) f[a[i]][j+k+1]+=(q[j]-q[j+1])*(h[k+1]-h[k]); } for(int i=1;i<=qi;i++) { scanf("%d%d",&a1,&a2); printf("%d\n",f[a2][a1]); } return 0; }kth
8.11聯考題解

