這節課難度超級大啊，基本上都是省選+NOI的題。

例1:

1801: [Ahoi2009]chess 中國象棋

Time Limit: 10 Sec Memory Limit: 64 MB Submit: 1868 Solved: 1075 [Submit][Status][Discuss]

Description

Input

Output

Sample Input

Sample Output

HINT

除了在3個格子中都放滿炮的的情況外，其它的都可以.
100%的數據中N,M不超過100 50%的數據中，N,M至少有一個數不超過8 30%的數據中，N,M均不超過6

分析：觀察50%的數據，發現有一個數非常小，符合狀壓dp的條件，於是我們考慮每一行怎麽放，用狀壓dp能過50分.

那麽怎麽樣才能通過全部分呢？狀壓dp比較耗時的原因是枚舉每一行的狀態用時太多，我們每次都要考慮每一列放或不放，要考慮2^m次，但是這道題只要求計數啊，所以我們完全不必記錄每一行到底怎麽放，我們只需要考慮有幾行怎麽放就可以了，也就是說，我們不必考慮每一行具體的怎麽放，我們只需要考慮每一行中有多少列不放，放一個，放兩個即可。

那麽設f[i][j][k]為前i行中有j列放1個，有k列放2個的方案數，可以發現每一行最多只能放兩個，那麽這些炮可以不放，放在只放了一個的列裏，放在沒有放的列裏，並考慮一下放幾個，狀態轉移方程就出來了，不過這個方程實在是太復雜，可以看代碼理解:

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>

using namespace std;

const int mod = 9999973
 
;

int n, m,ans;
long long f[110][110][110];

int C(int x)
{
    return x * (x - 1) / 2;
}

int main()
{
    scanf("%d%d", &n, &m);
    f[0][0][0] = 1;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 0; j <= m; j++)
        {
            for (int k = 0; k <= m; k++)
            {
                f[i][j][k] = (f[i][j][k] + f[i - 1][j][k]) % mod;   //不放
                if (j >= 1)
                    f[i][j][k] = (f[i][j][k] + f[i - 1][j - 1][k] * (m - j + 1 - k) % mod) % mod; //在沒有的列上放一個
                if (k >= 1)
                    f[i][j][k] = (f[i][j][k] + f[i - 1][j + 1][k - 1] * (j + 1) % mod) % mod; //在只有一個的列上放一個
                if (j >= 2)
                    f[i][j][k] = (f[i][j][k] + f[i - 1][j - 2][k] * C(m - j + 2 - k) % mod) % mod;   //在沒有的列上放二個
                if (k >= 2)
                    f[i][j][k] = (f[i][j][k] + f[i - 1][j + 2][k - 2] * C(j + 2) % mod) % mod;  //在只有一個的列上放二個
                if (k >= 1)
                    f[i][j][k] = (f[i][j][k] + f[i-1][j][k - 1] * j * (m - j - k + 1) % mod ) % mod; //在有一個和沒有的列上放二個
            }
        }
    }
    for (int i = 0; i <= m; i++)
        for (int j = 0; j <= m; j++)
            ans = (ans + f[n][i][j]) % mod;
    printf("%d\n", ans % mod);

    //while (1);
    return 0;
}

總結：有時候狀態記錄的不要太精細，特別是求方案數的，我們只需要記錄怎麽放的行數和列數就能做出來就完全不需要記錄到底是哪一行怎麽放。

例2：

分析：這個原題的數據範圍是非常非常小的，只不過這裏出的有點喪心病狂.這道題有點像背包，我們可以設f[i][j][k]表示前i首歌中用了y張唱片並且當前唱片長度用了k的最多放的歌曲的數目,轉移就很好辦了，如果ai > k,那麽只能不放或者試試放在上一個唱片裏。如果ai <= k,那麽可以不放或者放，狀態轉移長這樣：時間復雜度O(nmt),由於包含了t,完美爆掉.

那麽我們想，能不能不要記錄這個k,也就是只要前兩維，這樣就可以保證復雜度裏沒有t,但是如果不要第三維，我們怎麽知道當前唱片用了多少長度呢？我們完全可以開一個二元組，記錄答案和當前的k,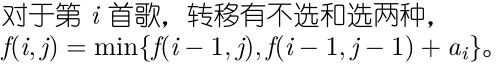,這裏的加法是唱片數和k同時相加，這樣我們就不需要枚舉k了，成功解決,復雜度O(nm).

總結：我們完全可以把設計的狀態中的某一維放進答案裏記錄，這樣可以精簡狀態.不過前提是這一維能通過其它的維度推出來.這個做法主要是應用於狀態設計中某一維過大，用來減少復雜度.

例3：

Description

方伯伯在自己的農田邊散步，他突然發現田裏的一排玉米非常的不美。
這排玉米一共有N株，它們的高度參差不齊。
方伯伯認為單調不下降序列很美，所以他決定先把一些玉米拔高，再把破壞美感的玉米拔除掉，使得剩下的玉米的高度構成一個單調不下降序列。
方伯伯可以選擇一個區間，把這個區間的玉米全部拔高1單位高度，他可以進行最多K次這樣的操作。拔玉米則可以隨意選擇一個集合的玉米拔掉。
問能最多剩多少株玉米，來構成一排美麗的玉米。

Input

第1行包含2個整數n，K，分別表示這排玉米的數目以及最多可進行多少次操作。
第2行包含n個整數，第i個數表示這排玉米，從左到右第i株玉米的高度ai。

Output

輸出1個整數，最多剩下的玉米數。

Sample Input

Sample Output

HINT

1 < N < 10000，1 < K ≤ 500，1 ≤ ai ≤5000

分析：這道題就是求一個LIS，只不過多了一個拔高的限制，那麽在原有的LISdp方程中加一個維度就好了，用f(i,j) 表示以第 i 株玉米結尾它被拔高了 j 次的最長序列長度。
f(i,j) = max{f(p,q) + 1}(0 ≤ p < i,0 ≤ q ≤ j,a [p] + q ≤a[i] + j)
現在來講一講為什麽有第二個限制，可以發現每次操作的右端點都必須是n,為什麽呢？因為如果不是n,那麽它就不會對右邊有貢獻，只會對左邊有貢獻，是n的話不會影響對左邊的貢獻，而p<i,所以一定有第二個限制。
不過這個算法復雜度是O(n^2*k^2)的，會超時，我們該怎麽優化呢？
可以發現這就是維護一個二維前綴最大值，對於前綴的操作可以用前綴和，也可以用樹狀數組，不過這個不滿足區間加減，所以我們用二維樹狀數組來維護就可以了。不過在操作的時候要倒序操作，以免狀態重復轉移.

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>

using namespace std;

int n, k,a[10010],c[10010][510],maxn,ans;

void add(int x, int y, int v)
{
    for (int i = x; i <= maxn; i += i & -i)
        for (int j = y; j <= k + 1; j += j & -j)
            c[i][j] = max(c[i][j], v);
}

int sum(int x, int y)
{
    int res = 0;
    for (int i = x; i; i -= i & -i)
        for (int j = y; j; j -= j & -j)
            res = max(res, c[i][j]);
    return res;
}

int main()
{
    scanf("%d%d", &n, &k);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
        maxn = max(maxn, a[i]);
    }
    maxn += k;  //因為可能會被增加k次，所以上限+k
    for (int i = 1; i <= n; i++)
        for (int j = k; j >= 0; j--)
        {
        int t = sum(a[i] + j, j + 1) + 1;  //至於為什麽要j+1,因為我們調用不能出現0，否則會死循環
        add(a[i] + j, j + 1, t);
        ans = max(t, ans);
        }
    printf("%d\n", ans);

    return 0;
}

總結：一些dp可以利用數據結構來加速優化，例如遇到區間可以考慮線段樹，前綴和，樹狀數組......

不過還可以考慮另外一種優化:

f(i,j) = max{f(p,q) + 1}(0 ≤ p < i,0 ≤ q ≤ j,a [p] + q ≤a [i] + j)。

f(i,j ? 1) = max{f(p,q) + 1}(0 ≤ p < i,0 ≤ q < j, a [p] + q < a [i] + j)。

可以發現f[i][j]從f[i][j-1]轉移而來限制條件只是多了一個q=j或a[p] + q = a[i] + j,那麽我們維護多個一維樹狀數組，就能夠通過查詢前綴最大值來求解.

總結：對於有限制條件的，我們可以通過其相鄰狀態的限制條件的不同來轉移，可能會有意想不到的效果，不過似乎這種優化很少見...

2017.8.12 dp課小結