Winter is here at the North and the White Walkers are close. John Snow has an army consisting of n soldiers. While the rest of the world is fighting for the Iron Throne, he is going to get ready for the attack of the White Walkers.

He has created a method to know how strong his army is. Let the i-th soldier’s strength be a_i. For some k he calls i₁,?i₂,?...,?i_k a clan if i₁?<?i₂?<?i₃?<?...?<?i_k and gcd(a_i1,?a_i2,?...,?a_ik)?>?1 . He calls the strength of that clan k·gcd(a_i1,?a_i2,?...,?a_ik). Then he defines the strength of his army by the sum of strengths of all possible clans.

Your task is to find the strength of his army. As the number may be very large, you have to print it modulo 1000000007 (10⁹?+?7).

Greatest common divisor (gcd) of a sequence of integers is the maximum possible integer so that each element of the sequence is divisible by it.

The first line contains integer n

The second line contains n integers a₁,?a₂,?...,?a_n (1?≤?a_i?≤?1000000) — denoting the strengths of his soldiers.

Print one integer — the strength of John Snow‘s army modulo 1000000007 (10⁹?+?7).

3
3 3 1

12

4
2 3 4 6

39

In the first sample the clans are {1},?{2},?{1,?2} so the answer will be 1·3?+?1·3?+?2·3?=?12

和今年多校之前一場的一道題目處理方法很相似。考慮每個gcd，如果某序列滿足gcd整除該序列的每一個數，那麽這個gcd就一定整除該序列的真正最大公因數。對於某數x，求x整除序列中每一個數的序列顯然比求x為序列gcd的序列個數容易的多，並且它們是有一定關系的，所以先求出對於每一個x，整除序列中每一個數的序列個數。顯然序列中的數都得從被x整除的數中選取，設有cnt個，則序列個數即為

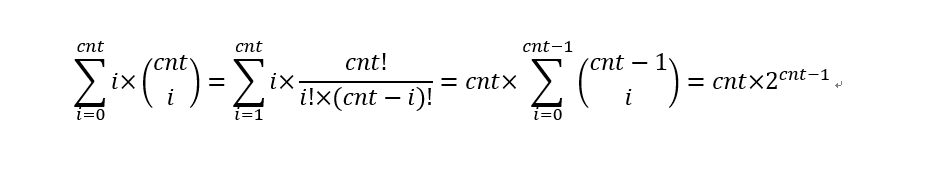
下面計算gcd的序列時采用從後往前做的策略，這樣就可以有效避免自己正序寫容斥的麻煩，因為我們從後往前求到現在求過的每一個數都是保證gcd恰好為此的序列個數，當前未求到的數x對應表示的是序列gcd為x，2*x,3*x……的個數之和，只需要把已經求出的部分全部減掉即可，得到的便是gcd為x的序列個數了。

 1 #include <cstdio>
 2 #include <iostream>
 3 #include <algorithm>
 4 #include <vector>
 5 #include <set>
 6 #include <map>
 7 #include <string>
 8 #include <cstring>
 9 #include <stack>
10 #include <queue>
11 #include <cmath>
12 #include <ctime>
13 #include<bitset>
14 #include <utility>
15 using namespace std;
16 #define REP(I,N) for (I=0;I<N;I++)
17 #define rREP(I,N) for (I=N-1;I>=0;I--)
18 #define rep(I,S,N) for (I=S;I<N;I++)
19 #define rrep(I,S,N) for (I=N-1;I>=S;I--)
20 #define FOR(I,S,N) for (I=S;I<=N;I++)
21 #define rFOR(I,S,N) for (I=N;I>=S;I--)
22 #define rank rankk
23 #define DFT FFT
24 typedef unsigned long long ull;
25 typedef long long ll;
26 const int INF=0x3f3f3f3f;
27 const ll INFF=0x3f3f3f3f3f3f3f3fll;
28 //const ll M=1e9+7;
29 const ll maxn=2e5+7;
30 const int MAXN=1005;
31 const int MAX=1e6+5;
32 const int MAX_N=MAX;
33 const int N=55;
34 const ll MOD=1e9+7;
35 //const double eps=0.00000001;
36 int gcd(int a,int b){return b?gcd(b,a%b):a;}
37 template<typename T>inline T abs(T a) {return a>0?a:-a;}
38 inline ll powMM(ll a,ll b,ll M){
39     ll ret=1;
40     a%=M;
41 //    b%=M;
42     while (b){
43         if (b&1) ret=ret*a%M;
44         b>>=1;
45         a=a*a%M;
46     }
47     return ret;
48 }
49 void open()
50 {
51     freopen("1004.in","r",stdin);
52     freopen("out.txt","w",stdout);
53 }
54 int n;
55 int num[MAX],tem,cnt[MAX],who,ans[MAX];
56 int an;
57 set<int>s;
58 set<int>::iterator it;
59 int main()
60 {
61     scanf("%d",&n);
62     for(int i=1;i<=n;i++)
63     {
64         scanf("%d",&tem);
65         num[tem]++;
66         s.insert(tem);
67     }
68     for(it=s.begin();it!=s.end();it++)
69     {
70         who=*it;
71         for(int i=1;i*i<=who;i++)
72         {
73             if(who%i==0)
74             {
75                 cnt[i]+=num[who];
76                 if(i*i!=who)
77                     cnt[who/i]+=num[who];
78             }
79         }
80     }
81 //    printf("who=%d\n",who);
82     for(int j=who;j>=2;j--)
83     {
84 //        printf("~~%d %d\n",j,cnt[j]);
85         if(!cnt[j])
86             continue;
87         ans[j]=(ll)powMM(2LL,(ll)cnt[j]-1,MOD)*cnt[j]%MOD;
88 //        printf("fin\n");
89         for(int i=2;i*j<=who;i++)
90         {
91 //            printf("!!%d %d\n",i,i*j);
92             ans[j]=(ans[j]-ans[i*j]+MOD)%MOD;
93         }
94         an=(an+(ll)j*ans[j]%MOD)%MOD;
95 //        printf("!!\n");
96     }
97     printf("%d\n",an);
98     return 0;
99 }

（容斥）Codeforces Round #428 (Div. 2) D. Winter is here