（參考文獻來自An Efficient Approach for Maintaining Association Rules based on Adjusting FP-tree Structure

Jia-Ling Koh and Shui-Feng Shieh Department of Information and Computer Education

其中有大量的刪減，如果想直奔主題，看幹貨，可直接從3、調整FP_tree的策略 [email protected]）

1、Introduction

數據挖掘在數據庫研究中引起了廣泛的關註，因為它在許多領域中有著廣泛應用。 在各種數據挖掘應用中，客戶交易中的挖掘關聯規則是重要的。客戶交易記錄通常由客戶ID，交易時間和交易中購買的所有項目組成。這種數據庫的挖掘關聯規則是找出所有的規則，如“購買項目X和Y的客戶中有n％的人在同一交易中也購買項目Z”，其中n，X，Y，Z最初是未知的。 這樣的規則對於定制營銷的決策是有用的。

已經提出了幾種有效的算法用於尋找頻繁項集，並且關聯規則是從頻繁項集推導出來的，如Apriori和DHP算法。這些“類Apriori”的算法受到（1）處理大量候選集（2）重復掃描數據庫的限制。 韓家煒提出了一種頻繁模式樹（FP-tree）結構，用於存儲關於頻繁模式壓縮結構和關鍵信息。此外，開發了一種稱為FP-Growth的算法，用於從FP-tree中挖掘完整的頻繁項集。這種方法避免了大量的候選集的產生和重復的數據庫掃描的代價，這被認為是挖掘頻繁項集的最有效的策略。

事務數據庫的更新可能會使現有規則無效或引入新規則。更新“關聯規則”以便更快的在更新的數據庫中找到新的頻繁項集集合。更新關聯規則的一個簡單的解決方案是重新挖掘整個更新的數據庫。然而，這種方法的無效性（或者說效率底下）是顯而易見的，因為在以前的挖掘中完成的所有計算都是浪費的。有人研究了如何者保留先前發現的關聯規則，並在此基礎上更新新的關聯規則，提出了在添加新的事務數據時增加更新關聯規則的FUP算法。為了解決一般情況的問題，包括數據庫中事務的插入，刪除和修改，FUP算法被修改並開發出FUP2算法。還有人提出了一種類似於FUP算法的增量更新技術，用於挖掘多層次關聯規則。作為“類Apriori“的算法，所有FUP系列都必須產生大量的候選，並反復掃描數據庫。

除了頻繁項目集之外，有人提出的增量更新技術還保留了附加信息。有人提出了一種增量挖掘算法，用於尋找頻繁的序列模式。在該算法中保留了前序列，其是具有較低支持閾值和上限閾值之間的支持的序列。需要從重新掃描原始數據庫時確定的下限閾值和上限閾值派生的綁定。在另一個算法中，負邊界與頻繁項集保持一致。 如果將負邊界外的項目集添加到頻繁項集或其負邊界，則該算法需要對整個數據庫進行全面掃描。

在本文中，我們提出一種稱為AFPIM（增量挖掘調整FP-tree）的算法，以便事務數據庫在添加，刪除或修改新事務時，以最小的計算量來有效地查找新的頻繁項集。 在我們的方法中，原始數據庫的FP-tree結構除了頻繁項目集之外都被維護。 在大多數情況下，不需要重新掃描整個數據庫，通過根據插入和刪除的事務調整之前的FP-tree來獲得更新的數據庫的FP-tree結構。 然後從新的FP-tree結構中挖掘更新數據庫的頻繁項集，並發現相應的關聯規則。

2、Problem Dwscription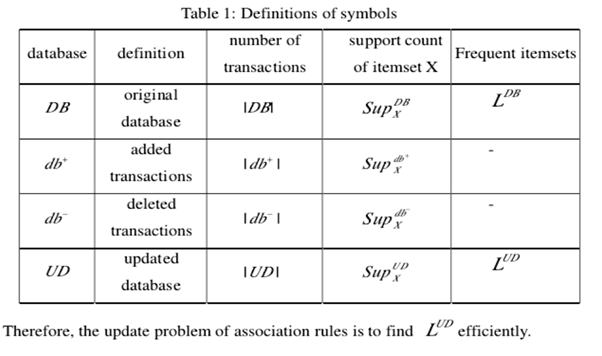

基本概念：

在本文中，應用了“前序列“（pre-large sequences）的概念。除了最小支持閾值之外，還指定了一個較小的閾值，稱為”預最低支持“（pre-minimum support）。對於數據庫中的每個項目X，如果其支持計數不小於最小支持，則將X命名為頻繁項。如果X的支持次數小於最小支持，並且不低於”預最低支持“，則X稱為“預先頻繁項”。否則，X是非頻繁的項目。在以下情況下，頻繁項目和預先頻繁項目被命名為“頻繁或預先頻繁項”。

為了有效解決更新問題，我們在挖掘原始數據庫DB後維護以下信息。

1.數據庫中的所有項目以及數據庫中的支持計數。
2.數據庫的FP樹，根據DB中的頻繁或預先頻繁的項目構建。
DB中的項目X是頻繁的，預先頻繁（pre-frequent）或在頻繁（in-frequents）的項目，它們將成為UD中的頻繁，預先頻繁或在頻繁的項目。

3、調整FP_tree的策略：

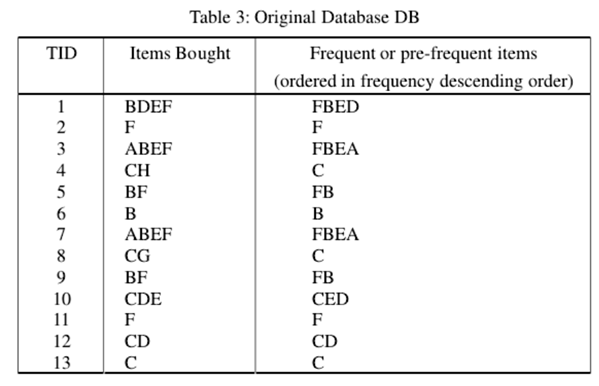
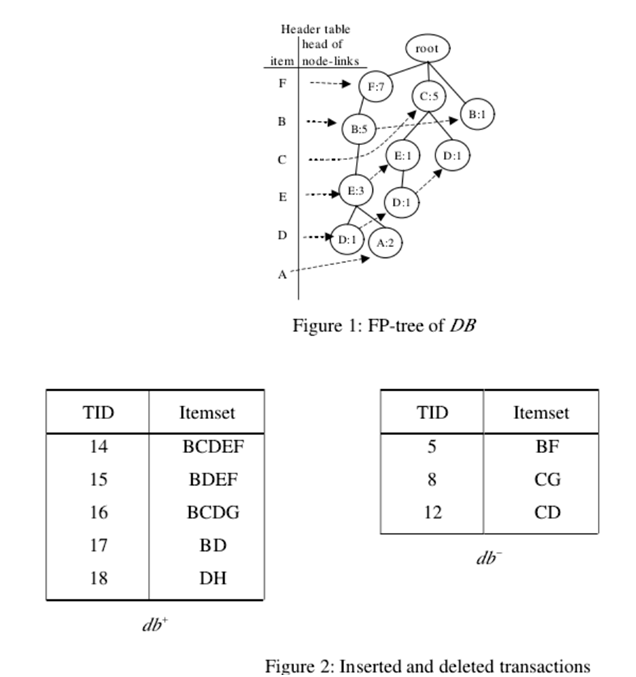
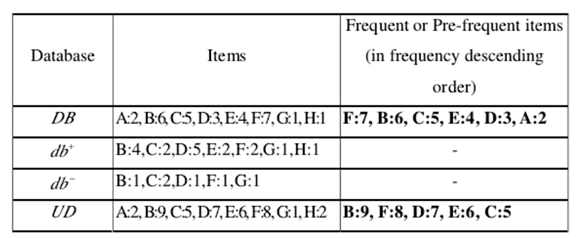
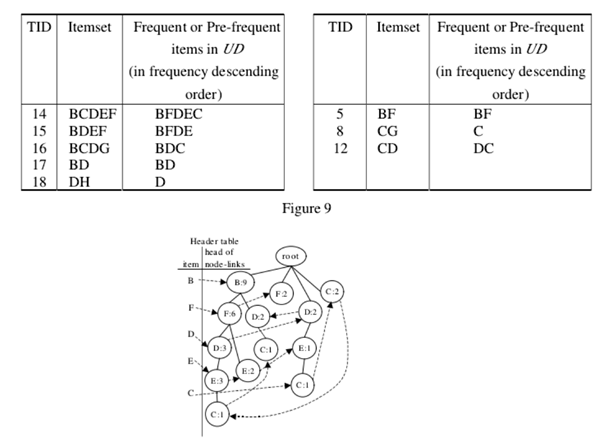
原始數據庫DB。 最小支持為0.2，預先最小支持（pre-minimum support）為0.15。A：2，B：6，C：5，D：3，E：4，F：7，G：1和H：1（：表示支持計數）。支持的項目不小於2（即13×0.15 = 1.95）是DB中的頻繁或預先頻繁的項目。 因此，A，B，C，D，E和F是DB中的頻繁項。 在按順序排列所有頻繁或預先頻繁的項目後，結果為F：7，B：6，C：5，E：4，D：3和A：2。然後插入5個事務，並從DB中刪除3個事務。db +和db-中的所有項目的支持計數都在上面。對於UD中的每個項目X，支持數可以通過簡單的計算獲得。 結果是A：2，B：9，C：5，D：7，E：6，F：8，G：1和H：2。在新數據庫UD中，預先頻繁或頻繁的項目必須具有不少於3的支持計數。因此，以頻率遞減順序顯示的UD中頻繁或頻繁的1項集是B：9，F：8，D：7，E：6和C：5。

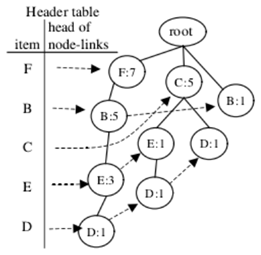
刪除非頻繁節點：

假設項目I在UD中非頻繁，表示I的節點必須從FP樹中刪除。 從項目I開始，在FP-tree頭部和跟隨I節點鏈接之後，可以逐個獲得表示I的所有節點。 對於每個節點N，使得N.item-name = I，將其子節點設置為其父節點的子節點，並從I節點鏈路中刪除N。 最後，刪除標題表中的I條目。A在UD中不是頻繁的或預先頻繁的項目。 因此，表示A的節點從FP樹中移除。

DB中支持數降序的頻繁或預先頻繁項目的列表，應用冒泡排序算法來確定在UD中滿足相鄰項目的支持降序的交換方式。 如上圖所示，需要進行4次交換，以調整DB中的支持降序以符合UD中的順序。 在決定要交換的項目對之後，在DB的FP-tree中，必須調整包含一對交換項目的路徑。 調整方法如下所述。假設在DB的FP-tree中存在路徑，其中節點Y是節點X的子節點，並且必須交換節點X和Y中表示的項目。 另外，節點P是X的父節點。如果X.count大於Y.count，執行步驟1到3。 否則，執行步驟2到3。
【步驟1】插入： 插入節點P的子節點X‘，其中X‘.count設置為X.count - Y.count。 X除了節點Y的所有子節點都被分配為X‘的子節點。 另外，X.count被重置為等於Y.count。
【步驟2】交換：分別交換節點X和節點Y的父鏈接和子鏈路。
【步驟3】合並：檢查是否存在P節點，表示為節點Z，Z.item-name = Y.item-name。 如果節點Z存在，則將Z.count相加到Y.count中，並且刪除節點Z。

第一次叠代調整：項目F和B的交換節點

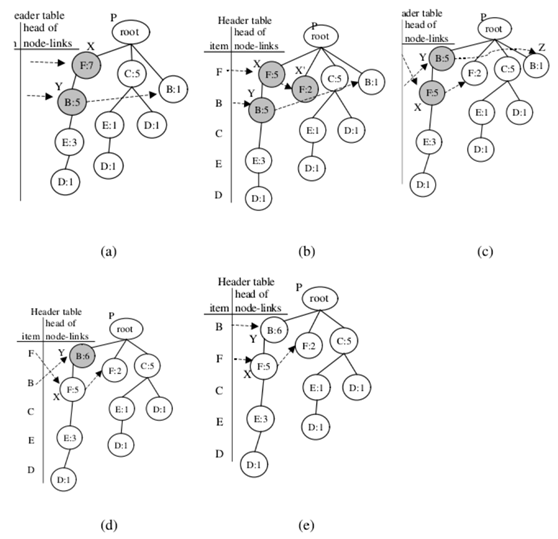
從FP-tree的頭表中，可以獲得項目F的節點鏈接。先來把攜帶項目名稱F的節點被表示為節點X，存在X的子節點Y，使得名稱為B。因此，執行調整方法。
（1）插入：對於X的父節點，在這種情況下，根節點插入一個子節點
節點X‘攜帶項目名稱F. X‘的計數字段分配為2，（即7-5）。此外，X.count被重新分配為等於Y.count，5。最後，將X‘插入到F的節點鏈接中。
（2）交換：交換節點X和節點Y。
（3）合並：存在根節點的另一個子節點Z，使得“Z”攜帶與”Y”相同的項目名稱B。因此，在節點中的計數值Z被合並到節點Y中，Z被去除。

得到攜帶項目名稱F的下一個節點。但是，該節點沒有名稱為B的子節點，因此已到達項目F的節點鏈接的終端，這個叠代是完整的；

第二次調整叠代：項目C和E的交換節點

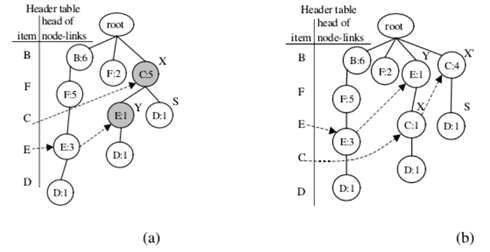
與第一次叠代的過程類似，攜帶項目名稱C的第一個節點是表示為節點X，並且發現其攜帶項目名稱E的子節點Y。 然後進行調整方法。 在這種情況下，節點X除節點Y之外還有另一個子節點S.因此，節點S被分配為新添加的節點X‘的子節點；

第三次調整：項目C和D的交換節點：

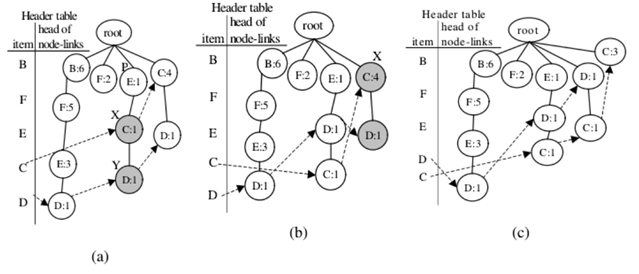
攜帶項目名稱C的第一個節點及其子節點攜帶項目名稱D.，分別表示為節點X和Y在這種情況下，X.count等於Y.count。 因此，只有步驟2和步驟3進行調整方法。下一組項目C和D的節點，表示為節點X和Y執行調整方法並進行交換標題表中項目F和B的條目；

第四次叠代調整：項目E和D的交換節點。

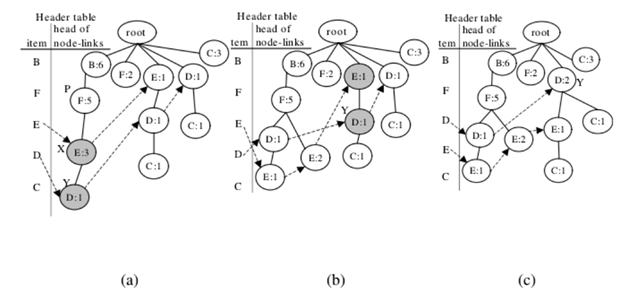
4、插入或者刪除數據：

在FP-tree裏面調整節點的路徑後，所得FP-tree中的每個路徑都遵循UD中頻繁或前綴頻繁項的頻率降序。 對於db +中的每個事務T，選擇T中包含的UD的頻繁或預先頻繁的項目，並按降序排序。 事務T將被插入到FP-tree中作為構建FP-tree的過程。 同樣，每個事務T在db-從FP樹中刪除。

5、AFPIM算法：

基於上述描述的策略，我們有以下AFPIM算法調整增量挖掘頻繁項集的FP-tree結構。
【步驟1】閱讀DB中的項目及其DB中的支持計數。
【步驟2】掃描數據庫db+和db- 一次，分別列出在db+和db-所有項目及其支持數。對於每個項目X，計算UD中的X的支持計數根據公式：

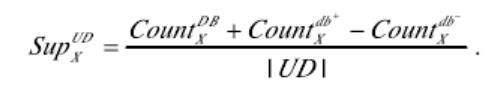
然後在UD中收集頻繁或預先頻繁的項目。
【步驟3】判斷是否所有的UD頻繁項目是否都在DB的FP-tree中覆蓋。
【步驟3.1】如果在FP-tree中存在UD的頻繁項目，則整個UD需要要掃描一次，以便根據頻繁重建UD的FP樹或UD中的前綴項目。
【步驟3.2】否則，讀入存儲的數據庫的FP-tree。
【步驟3.2.1】對於UD中的每個不頻繁的項目，從中刪除相應的節點FP樹。
【步驟3.2.2】根據DB和UD中的支持數降序的排列順序，應用冒泡排序算法來交換項目順序。然後重復使用路徑調整方法來調整結構FP-tree中的路徑。
【步驟3.2.3】掃描數據庫db+ 和db- 第二次，調用函數tree_insert_delete插入事務db+和刪除事務db- 。最後，得到了所得到的UD的FP樹。
【步驟4】應用FP-Growth算法和TD-FP-Growth算法分別從UD的FP樹中找出UD中的頻繁項集

偽代碼：

關聯規則挖掘算法AFPIM