對於選擇排序算法，其實有很大的一個問題：在每趟的比較過程中，程序一旦發現某個數據比第一位的數據小，立即交換它們。這保證在每趟比較的所有比較過的數據中，第1位的數據永遠是最小的，單著沒有太大必要，反而增加了交換的次數，導致算法效率降低。

改進優化後的算法如下：

public class SelectSort {
    public static void selectSort(DataWrap[] data)
    {
        System.out.println("開始排序");
        int length = data.length;
        
 
//依次進行n-1趟比較，第i趟比較將第i大的值選出來放在i位置上
        for(int i = 0;i < length-1; i++ )
        {
            //mindex永遠保存本趟比較中最小值得索引
            int mindex = i;
            //第i個數只需要與它後面的數比較
            for(int j = i+1;j < length;j++)
            {
                //如果mindex上的數據大於j位置上的數據
                if(data[mindex].compareTo(data[j]) > 0)
                {
                    
 
//將j的值賦給mindex
                    mindex = j;
                }
            }
            //每次比較最多交換依次
            if(mindex != i)
            {
                DataWrap tep = data[i];
                data[i] = data[mindex];
                data[mindex] = tep;
            }
            System.out.println(java.util.Arrays.toString(data));
        }
    }
    
 
public static void main(String[] args) {
        DataWrap[] data = {
                new DataWrap(21, ""),
                new DataWrap(30, ""),
                new DataWrap(49, ""),
                new DataWrap(30, ""),
                new DataWrap(16, ""),
                new DataWrap(9, "")
        };
        System.out.println("排序之前:\n" + java.util.Arrays.toString(data));
        selectSort(data);
        System.out.println("排序之後:\n" + java.util.Arrays.toString(data));
    }
}
class DataWrap implements Comparable<DataWrap>
{
    int data;
    String flag;
    public DataWrap(int data, String flag) {
        this.data = data;
        this.flag = flag;
    }
    
    public String toString() {
        return data+flag;
    }
    public int compareTo(DataWrap dw) {
        return this.data > dw.data ? 1 : (this.data > dw.data ? 0 : -1);
    }
}

結果圖：

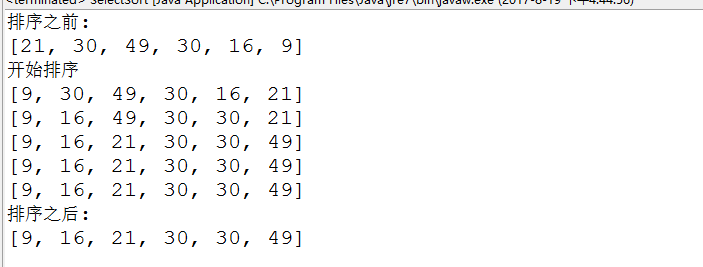
在這種排序規則下，每趟比較的目的只是找出本題比較中的最小數據的索引——也就是上面程序中的midIndex變量所保存的值。當本趟比較的第i位（由i變量保存）與midIndex不相等時，交換i和midIndex兩處的數據。

從結果圖中可以看出，直接選擇排序的第n趟比較至多交換一次，永遠總是拿n-1位的數據和中間某項數據（本趟比較中最小的數據）進行交流。如果本趟比較時第n-1位（本趟比較的第1位）數據已經是最小，那就無需交換。

對於直接選擇排序算法而言，假設有n項數據，數據交換的次數最多有n-1次，但程序比較測次數較多，總體來說，其時間效率為O（n2）。空間效率很高，它只需要一個附加程序單元用於交換，其空間效率為O(1)。直接選擇排序是不穩定的。

優化的選擇排序算法分析