2017中國大學生程序設計競賽 - 網絡選拔賽 HDU 6155 Subsequence Count 矩陣快速冪
阿新 • • 發佈:2017-08-20
htm 遞推關系 更新 ble pri -1 wap html sin
題目鏈接:http://acm.hdu.edu.cn/showproblem.php?pid=6155
題意:
題解來自:http://www.cnblogs.com/iRedBean/p/7398272.html
先考慮dp求01串的不同子序列的個數。
dp[i][j]表示用前i個字符組成的以j為結尾的01串個數。
如果第i個字符為0,則dp[i][0] = dp[i-1][1] + dp[i-1][0] + 1,dp[i][1] = dp[i-1][1]
如果第i個字符為1,則dp[i][1] = dp[i-1][1] + dp[i-1][0] + 1,dp[i][0] = dp[i-1][0]
顯然這是線性遞推,我們考慮如何用矩陣表示這種遞推關系。
下面分別對應加入一個字符0或1時表示遞推關系的矩陣。
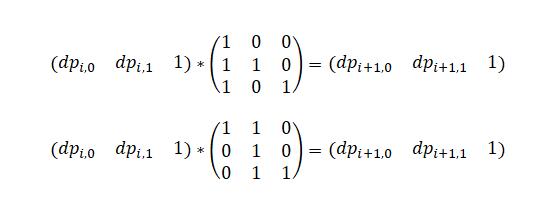
然後用線段樹維護每個區間的矩陣乘積就可以解決查詢操作了。
對於修改操作,我們給區間維護一個flip標記,表示該區間是否要翻轉,用線段樹區間更新的方法去更新flip標記就好了。
將一個區間翻轉後,它對應矩陣也要發生改變,這裏我們只要將矩陣的第一列與第二列交換後再將第一行與第二行交換就好了。
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+6;
const int mod = 1e9+7;
typedef long long LL;
struct Matrix{
LL maze[3][3];
friend Matrix operator*(const Matrix& a, const Matrix& b){
Matrix c;
for(int i=0; i<3; i++){
for(int j=0; j<3; j++){
c.maze[i][j]=0;
for(int k=0; k<3; k++){
c.maze[i][j]+=a.maze[i][k]*b.maze[k][j];
c.maze[i][j]%=mod;
}
}
}
return c;
}
};
const Matrix m[2]={{1,0,0,1,1,0,1,0,1},{1,1,0,0,1,0,0,1,1}};
Matrix T[maxn<<2];
bool flip[maxn<<2];
char s[maxn];
void build(int l, int r, int rt){
flip[rt] = 0;
if(l == r){
T[rt] = m[s[l]-‘0‘];
return;
}
int mid = (l+r)>>1;
build(l, mid, rt*2);
build(mid+1, r, rt*2+1);
T[rt] = T[rt*2]*T[rt*2+1];
}
void Flip(Matrix &mat){
swap(mat.maze[0][0],mat.maze[0][1]);
swap(mat.maze[1][0],mat.maze[1][1]);
swap(mat.maze[2][0],mat.maze[2][1]);
swap(mat.maze[0][0],mat.maze[1][0]);
swap(mat.maze[0][1],mat.maze[1][1]);
swap(mat.maze[0][2],mat.maze[1][2]);
}
void pushdown(int rt){
if(flip[rt]){
flip[rt*2]^=flip[rt];
flip[rt*2+1]^=flip[rt];
Flip(T[rt*2]);
Flip(T[rt*2+1]);
flip[rt]=false;
}
}
void update(int L, int R, int l, int r, int rt){
if(L<=l&&r<=R){
flip[rt]^=1;
Flip(T[rt]);
return;
}
pushdown(rt);
int mid=(l+r)/2;
if(R<=mid) update(L,R,l,mid,rt*2);
else if(L>mid) update(L,R,mid+1,r,rt*2+1);
else{
update(L,mid,l,mid,rt*2);
update(mid+1,R,mid+1,r,rt*2+1);
}
T[rt]=T[rt*2]*T[rt*2+1];
}
Matrix query(int L, int R, int l, int r, int rt){
if(L<=l&&r<=R){
return T[rt];
}
pushdown(rt);
int mid=(l+r)/2;
if(R<=mid) return query(L,R,l,mid,rt*2);
else if(L>mid) return query(L,R,mid+1,r,rt*2+1);
else return query(L,mid,l,mid,rt*2)*query(mid+1,R,mid+1,r,rt*2+1);
}
int main()
{
int T,n,q;
scanf("%d", &T);
while(T--)
{
scanf("%d%d",&n,&q);
scanf("%s",s+1);
build(1,n,1);
while(q--)
{
int op,l,r;
scanf("%d%d%d",&op,&l,&r);
if(op==1) update(l,r,1,n,1);
else{
Matrix ret = query(l,r,1,n,1);
printf("%lld\n", (ret.maze[2][0]+ret.maze[2][1])%mod);
}
}
}
return 0;
}
2017中國大學生程序設計競賽 - 網絡選拔賽 HDU 6155 Subsequence Count 矩陣快速冪
