分布式系統的事務處理
當我們在生產線上用一臺服務器來提供數據服務的時候,我會遇到如下的兩個問題:
1)一臺服務器的性能不足以提供足夠的能力服務於所有的網絡請求。
2)我們總是害怕我們的這臺服務器停機,造成服務不可用或是數據丟失。
於是我們不得不對我們的服務器進行擴展,加入更多的機器來分擔性能上的問題,以及來解決單點故障問題。 通常,我們會通過兩種手段來擴展我們的數據服務:
1)數據分區:就是把數據分塊放在不同的服務器上(如:uid % 16,一致性哈希等)。
2)數據鏡像:讓所有的服務器都有相同的數據,提供相當的服務。
對於第一種情況,我們無法解決數據丟失的問題,單臺服務器出問題時,會有部分數據丟失。所以,數據服務的高可用性只能通過第二種方法來完成——數據的冗余存儲
- 從A帳號中把余額讀出來。
- 對A帳號做減法操作。
- 把結果寫回A帳號中。
- 從B帳號中把余額讀出來。
- 對B帳號做加法操作。
- 把結果寫回B帳號中。
為了數據的一致性,這6件事,要麽都成功做完,要麽都不成功,而且這個操作的過程中,對A、B帳號的其它訪問必需鎖死,所謂鎖死就是要排除其它的讀寫操作,不然會有臟數據的問題,這就是事務。那麽,我們在加入了更多的機器後,這個事情會變得復雜起來:
1)在數據分區的方案中:如果A帳號和B帳號的數據不在同一臺服務器上怎麽辦?我們需要一個跨機器的事務處理。也就是說,如果A的扣錢成功了,但B的加錢不成功,我們還要把A的操作給回滾回去。這在跨機器的情況下,就變得比較復雜了。
2)在數據鏡像的方案中:A帳號和B帳號間的匯款是可以在一臺機器上完成的,但是別忘了我們有多臺機器存在A帳號和B帳號的副本。如果對A帳號的匯錢有兩個並發操作(要匯給B和C),這兩個操作發生在不同的兩臺服務器上怎麽辦?也就是說,在數據鏡像中,在不同的服務器上對同一個數據的寫操作怎麽保證其一致性,保證數據不沖突?
同時,我們還要考慮性能的因素,如果不考慮性能的話,事務得到保證並不困難,系統慢一點就行了。除了考慮性能外,我們還要考慮可用性,也就是說,一臺機器沒了,數據不丟失,服務可由別的機器繼續提供。 於是,我們需要重點考慮下面的這麽幾個情況:
1)容災:數據不丟、結點的Failover
2)數據的一致性:事務處理
3)性能:吞吐量 、 響應時間
前面說過,要解決數據不丟,只能通過數據冗余的方法,就算是數據分區,每個區也需要進行數據冗余處理。這就是數據副本:當出現某個節點的數據丟失時可以從副本讀到,數據副本是分布式系統解決數據丟失異常的唯一手段。所以,在這篇文章中,簡單起見,我們只討論在數據冗余情況下考慮數據的一致性和性能的問題。簡單說來:
1)要想讓數據有高可用性,就得寫多份數據。
2)寫多份的問題會導致數據一致性的問題。
3)數據一致性的問題又會引發性能問題
這就是軟件開發,按下了葫蘆起了瓢。
一致性模型
說起數據一致性來說,簡單說有三種類型(當然,如果細分的話,還有很多一致性模型,如:順序一致性,FIFO一致性,會話一致性,單讀一致性,單寫一致性,但為了本文的簡單易讀,我只說下面三種):
1)Weak 弱一致性:當你寫入一個新值後,讀操作在數據副本上可能讀出來,也可能讀不出來。比如:某些cache系統,網絡遊戲其它玩家的數據和你沒什麽關系,VOIP這樣的系統,或是百度搜索引擎(呵呵)。
2)Eventually 最終一致性:當你寫入一個新值後,有可能讀不出來,但在某個時間窗口之後保證最終能讀出來。比如:DNS,電子郵件、Amazon S3,Google搜索引擎這樣的系統。
3)Strong 強一致性:新的數據一旦寫入,在任意副本任意時刻都能讀到新值。比如:文件系統,RDBMS,Azure Table都是強一致性的。
從這三種一致型的模型上來說,我們可以看到,Weak和Eventually一般來說是異步冗余的,而Strong一般來說是同步冗余的,異步的通常意味著更好的性能,但也意味著更復雜的狀態控制。同步意味著簡單,但也意味著性能下降。 好,讓我們由淺入深,一步一步地來看有哪些技術:
Master-Slave
首先是Master-Slave結構,對於這種加構,Slave一般是Master的備份。在這樣的系統中,一般是如下設計的:
1)讀寫請求都由Master負責。
2)寫請求寫到Master上後,由Master同步到Slave上。
從Master同步到Slave上,你可以使用異步,也可以使用同步,可以使用Master來push,也可以使用Slave來pull。 通常來說是Slave來周期性的pull,所以,是最終一致性。這個設計的問題是,如果Master在pull周期內垮掉了,那麽會導致這個時間片內的數據丟失。如果你不想讓數據丟掉,Slave只能成為Read-Only的方式等Master恢復。
當然,如果你可以容忍數據丟掉的話,你可以馬上讓Slave代替Master工作(對於只負責計算的結點來說,沒有數據一致性和數據丟失的問題,Master-Slave的方式就可以解決單點問題了) 當然,Master Slave也可以是強一致性的, 比如:當我們寫Master的時候,Master負責先寫自己,等成功後,再寫Slave,兩者都成功後返回成功,整個過程是同步的,如果寫Slave失敗了,那麽兩種方法,一種是標記Slave不可用報錯並繼續服務(等Slave恢復後同步Master的數據,可以有多個Slave,這樣少一個,還有備份,就像前面說的寫三份那樣),另一種是回滾自己並返回寫失敗。(註:一般不先寫Slave,因為如果寫Master自己失敗後,還要回滾Slave,此時如果回滾Slave失敗,就得手工訂正數據了)你可以看到,如果Master-Slave需要做成強一致性有多復雜。
Master-Master
Master-Master,又叫Multi-master,是指一個系統存在兩個或多個Master,每個Master都提供read-write服務。這個模型是Master-Slave的加強版,數據間同步一般是通過Master間的異步完成,所以是最終一致性。 Master-Master的好處是,一臺Master掛了,別的Master可以正常做讀寫服務,他和Master-Slave一樣,當數據沒有被復制到別的Master上時,數據會丟失。很多數據庫都支持Master-Master的Replication的機制。
另外,如果多個Master對同一個數據進行修改的時候,這個模型的惡夢就出現了——對數據間的沖突合並,這並不是一件容易的事情。看看Dynamo的Vector Clock的設計(記錄數據的版本號和修改者)就知道這個事並不那麽簡單,而且Dynamo對數據沖突這個事是交給用戶自己搞的。就像我們的SVN源碼沖突一樣,對於同一行代碼的沖突,只能交給開發者自己來處理。(在本文後後面會討論一下Dynamo的Vector Clock)
Two/Three Phase Commit
這個協議的縮寫又叫2PC,中文叫兩階段提交。在分布式系統中,每個節點雖然可以知曉自己的操作時成功或者失敗,卻無法知道其他節點的操作的成功或失敗。當一個事務跨越多個節點時,為了保持事務的ACID特性,需要引入一個作為協調者的組件來統一掌控所有節點(稱作參與者)的操作結果並最終指示這些節點是否要把操作結果進行真正的提交(比如將更新後的數據寫入磁盤等等)。 兩階段提交的算法如下:
第一階段:
- 協調者會問所有的參與者結點,是否可以執行提交操作。
- 各個參與者開始事務執行的準備工作:如:為資源上鎖,預留資源,寫undo/redo log……
- 參與者響應協調者,如果事務的準備工作成功,則回應“可以提交”,否則回應“拒絕提交”。
第二階段:
- 如果所有的參與者都回應“可以提交”,那麽,協調者向所有的參與者發送“正式提交”的命令。參與者完成正式提交,並釋放所有資源,然後回應“完成”,協調者收集各結點的“完成”回應後結束這個Global Transaction。
- 如果有一個參與者回應“拒絕提交”,那麽,協調者向所有的參與者發送“回滾操作”,並釋放所有資源,然後回應“回滾完成”,協調者收集各結點的“回滾”回應後,取消這個Global Transaction。
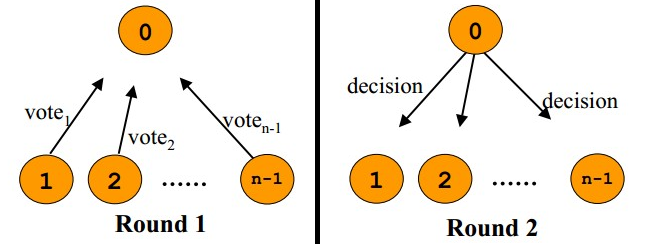
我們可以看到,2PC說白了就是第一階段做Vote,第二階段做決定的一個算法,也可以看到2PC這個事是強一致性的算法。在前面我們討論過Master-Slave的強一致性策略,和2PC有點相似,只不過2PC更為保守一些——先嘗試再提交。 2PC用的是比較多的,在一些系統設計中,會串聯一系列的調用,比如:A -> B -> C -> D,每一步都會分配一些資源或改寫一些數據。比如我們B2C網上購物的下單操作在後臺會有一系列的流程需要做。如果我們一步一步地做,就會出現這樣的問題,如果某一步做不下去了,那麽前面每一次所分配的資源需要做反向操作把他們都回收掉,所以,操作起來比較復雜。現在很多處理流程(Workflow)都會借鑒2PC這個算法,使用 try -> confirm的流程來確保整個流程的能夠成功完成。 舉個通俗的例子,西方教堂結婚的時候,都有這樣的橋段:
1)牧師分別問新郎和新娘:你是否願意……不管生老病死……(詢問階段)
2)當新郎和新娘都回答願意後(鎖定一生的資源),牧師就會說:我宣布你們……(事務提交)
這是多麽經典的一個兩階段提交的事務處理。 另外,我們也可以看到其中的一些問題, A)其中一個是同步阻塞操作,這個事情必然會非常大地影響性能。 B)另一個主要的問題是在TimeOut上,比如,
1)如果第一階段中,參與者沒有收到詢問請求,或是參與者的回應沒有到達協調者。那麽,需要協調者做超時處理,一旦超時,可以當作失敗,也可以重試。
2)如果第二階段中,正式提交發出後,如果有的參與者沒有收到,或是參與者提交/回滾後的確認信息沒有返回,一旦參與者的回應超時,要麽重試,要麽把那個參與者標記為問題結點剔除整個集群,這樣可以保證服務結點都是數據一致性的。
3)糟糕的情況是,第二階段中,如果參與者收不到協調者的commit/fallback指令,參與者將處於“狀態未知”階段,參與者完全不知道要怎麽辦,比如:如果所有的參與者完成第一階段的回復後(可能全部yes,可能全部no,可能部分yes部分no),如果協調者在這個時候掛掉了。那麽所有的結點完全不知道怎麽辦(問別的參與者都不行)。為了一致性,要麽死等協調者,要麽重發第一階段的yes/no命令。
兩段提交最大的問題就是第3)項,如果第一階段完成後,參與者在第二階沒有收到決策,那麽數據結點會進入“不知所措”的狀態,這個狀態會block住整個事務。也就是說,協調者Coordinator對於事務的完成非常重要,Coordinator的可用性是個關鍵。 因些,我們引入三段提交,三段提交在Wikipedia上的描述如下,他把二段提交的第一個段break成了兩段:詢問,然後再鎖資源。最後真正提交。三段提交的示意圖如下:
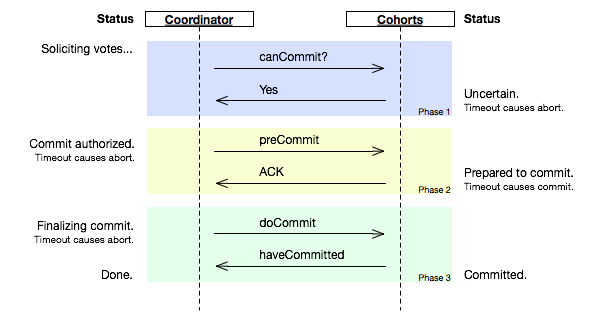
三段提交的核心理念是:在詢問的時候並不鎖定資源,除非所有人都同意了,才開始鎖資源。
理論上來說,如果第一階段所有的結點返回成功,那麽有理由相信成功提交的概率很大。這樣一來,可以降低參與者Cohorts的狀態未知的概率。也就是說,一旦參與者收到了PreCommit,意味他知道大家其實都同意修改了。這一點很重要。下面我們來看一下3PC的狀態遷移圖:(註意圖中的虛線,那些F,T是Failuer或Timeout,其中的:狀態含義是 q – Query,a – Abort,w – Wait,p – PreCommit,c – Commit)
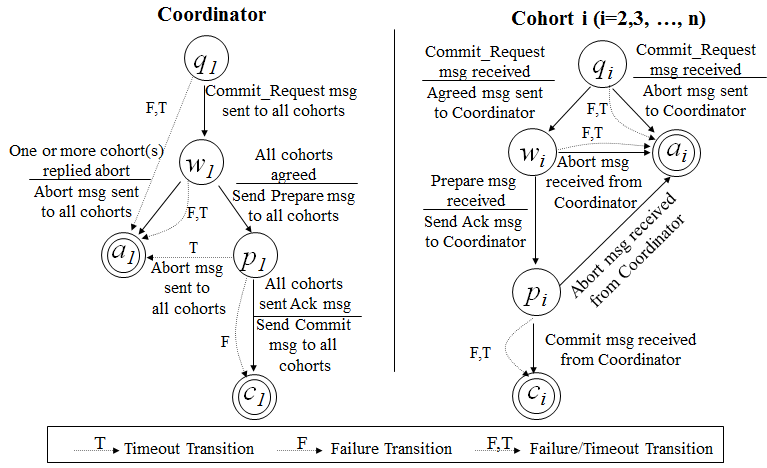
從上圖的狀態變化圖我們可以從虛線(那些F,T是Failuer或Timeout)看到——如果結點處在P狀態(PreCommit)的時候發生了F/T的問題,三段提交比兩段提交的好處是,三段提交可以繼續直接把狀態變成C狀態(Commit),而兩段提交則不知所措。
其實,三段提交是一個很復雜的事情,實現起來相當難,而且也有一些問題。
看到這裏,我相信你有很多很多的問題,你一定在思考2PC/3PC中各種各樣的失敗場景,你會發現Timeout是個非常難處理的事情,因為網絡上的Timeout在很多時候讓你無所事從,你也不知道對方是做了還是沒有做。於是你好好的一個狀態機就因為Timeout成了個擺設。
一個網絡服務會有三種狀態:1)Success,2)Failure,3)Timeout,第三個絕對是惡夢,尤其在你需要維護狀態的時候。
Two Generals Problem(兩將軍問題)
Two Generals Problem 兩將軍問題是這麽一個思維性實驗問題: 有兩支軍隊,它們分別有一位將軍領導,現在準備攻擊一座修築了防禦工事的城市。這兩支軍隊都駐紮在那座城市的附近,分占一座山頭。一道山谷把兩座山分隔開來,並且兩位將軍唯一的通信方式就是派各自的信使來往於山谷兩邊。不幸的是,這個山谷已經被那座城市的保衛者占領,並且存在一種可能,那就是任何被派出的信使通過山谷是會被捕。 請註意,雖然兩位將軍已經就攻擊那座城市達成共識,但在他們各自占領山頭陣地之前,並沒有就進攻時間達成共識。兩位將軍必須讓自己的軍隊同時進攻城市才能取得成功。因此,他們必須互相溝通,以確定一個時間來攻擊,並同意就在那時攻擊。如果只有一個將軍進行攻擊,那麽這將是一個災難性的失敗。 這個思維實驗就包括考慮他們如何去做這件事情。下面是我們的思考:
1)第一位將軍先發送一段消息“讓我們在上午9點開始進攻”。然而,一旦信使被派遣,他是否通過了山谷,第一位將軍就不得而知了。任何一點的不確定性都會使得第一位將軍攻擊猶豫,因為如果第二位將軍不能在同一時刻發動攻擊,那座城市的駐軍就會擊退他的軍隊的進攻,導致他的軍對被摧毀。
2)知道了這一點,第二位將軍就需要發送一個確認回條:“我收到您的郵件,並會在9點的攻擊。”但是,如果帶著確認消息的信使被抓怎麽辦?所以第二位將軍會猶豫自己的確認消息是否能到達。
3)於是,似乎我們還要讓第一位將軍再發送一條確認消息——“我收到了你的確認”。然而,如果這位信使被抓怎麽辦呢?
4)這樣一來,是不是我們還要第二位將軍發送一個“確認收到你的確認”的信息。
靠,於是你會發現,這事情很快就發展成為不管發送多少個確認消息,都沒有辦法來保證兩位將軍有足夠的自信自己的信使沒有被敵軍捕獲。
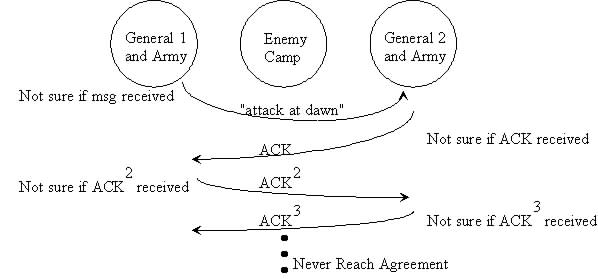
這個問題是無解的。兩個將軍問題和它的無解證明首先由E.A.Akkoyunlu,K.Ekanadham和R.V.Huber於1975年在《一些限制與折衷的網絡通信設計》一文中發表,就在這篇文章的第73頁中一段描述兩個黑幫之間的通信中被闡明。 1978年,在Jim Gray的《數據庫操作系統註意事項》一書中(從第465頁開始)被命名為兩個將軍悖論。作為兩個將軍問題的定義和無解性的證明的來源,這一參考被廣泛提及。
這個實驗意在闡明:試圖通過建立在一個不可靠的連接上的交流來協調一項行動的隱患和設計上的巨大挑戰。
從工程上來說,一個解決兩個將軍問題的實際方法是使用一個能夠承受通信信道不可靠性的方案,並不試圖去消除這個不可靠性,但要將不可靠性削減到一個可以接受的程度。比如,第一位將軍排出了100位信使並預計他們都被捕的可能性很小。在這種情況下,不管第二位將軍是否會攻擊或者受到任何消息,第一位將軍都會進行攻擊。另外,第一位將軍可以發送一個消息流,而第二位將軍可以對其中的每一條消息發送一個確認消息,這樣如果每條消息都被接收到,兩位將軍會感覺更好。然而我們可以從證明中看出,他們倆都不能肯定這個攻擊是可以協調的。他們沒有算法可用(比如,收到4條以上的消息就攻擊)能夠確保防止僅有一方攻擊。再者,第一位將軍還可以為每條消息編號,說這是1號,2號……直到n號。這種方法能讓第二位將軍知道通信信道到底有多可靠,並且返回合適的數量的消息來確保最後一條消息被接收到。如果信道是可靠的話,只要一條消息就行了,其余的就幫不上什麽忙了。最後一條和第一條消息丟失的概率是相等的。
兩將軍問題可以擴展成更變態的拜占庭將軍問題 (Byzantine Generals Problem),其故事背景是這樣的:拜占庭位於現在土耳其的伊斯坦布爾,是東羅馬帝國的首都。由於當時拜占庭羅馬帝國國土遼闊,為了防禦目的,因此每個軍隊都分隔很遠,將軍與將軍之間只能靠信差傳消息。 在戰爭的時候,拜占庭軍隊內所有將軍必需達成一致的共識,決定是否有贏的機會才去攻打敵人的陣營。但是,軍隊可能有叛徒和敵軍間諜,這些叛徒將軍們會擾亂或左右決策的過程。這時候,在已知有成員謀反的情況下,其余忠誠的將軍在不受叛徒的影響下如何達成一致的協議,這就是拜占庭將軍問題。
Paxos算法
Wikipedia上的各種Paxos算法的描述非常詳細,大家可以去圍觀一下。
Paxos 算法解決的問題是在一個可能發生上述異常的分布式系統中如何就某個值達成一致,保證不論發生以上任何異常,都不會破壞決議的一致性。一個典型的場景是,在一個分布式數據庫系統中,如果各節點的初始狀態一致,每個節點都執行相同的操作序列,那麽他們最後能得到一個一致的狀態。為保證每個節點執行相同的命令序列,需要在每一條指令上執行一個「一致性算法」以保證每個節點看到的指令一致。一個通用的一致性算法可以應用在許多場景中,是分布式計算中的重要問題。從20世紀80年代起對於一致性算法的研究就沒有停止過。
Notes:Paxos算法是萊斯利·蘭伯特(Leslie Lamport,就是 LaTeX 中的”La”,此人現在在微軟研究院)於1990年提出的一種基於消息傳遞的一致性算法。由於算法難以理解起初並沒有引起人們的重視,使Lamport在八年後1998年重新發表到ACM Transactions on Computer Systems上(The Part-Time Parliament)。即便如此paxos算法還是沒有得到重視,2001年Lamport 覺得同行無法接受他的幽默感,於是用容易接受的方法重新表述了一遍(Paxos Made Simple)。可見Lamport對Paxos算法情有獨鐘。近幾年Paxos算法的普遍使用也證明它在分布式一致性算法中的重要地位。2006年Google的三篇論文初現“雲”的端倪,其中的Chubby Lock服務使用Paxos作為Chubby Cell中的一致性算法,Paxos的人氣從此一路狂飆。(Lamport 本人在 他的blog 中描寫了他用9年時間發表這個算法的前前後後)
註:Amazon的AWS中,所有的雲服務都基於一個ALF(Async Lock Framework)的框架實現的,這個ALF用的就是Paxos算法。我在Amazon的時候,看內部的分享視頻時,設計者在內部的Principle Talk裏說他參考了ZooKeeper的方法,但他用了另一種比ZooKeeper更易讀的方式實現了這個算法。
簡單說來,Paxos的目的是讓整個集群的結點對某個值的變更達成一致。Paxos算法基本上來說是個民主選舉的算法——大多數的決定會成個整個集群的統一決定。任何一個點都可以提出要修改某個數據的提案,是否通過這個提案取決於這個集群中是否有超過半數的結點同意(所以Paxos算法需要集群中的結點是單數)。
這個算法有兩個階段(假設這個有三個結點:A,B,C):
第一階段:Prepare階段
A把申請修改的請求Prepare Request發給所有的結點A,B,C。註意,Paxos算法會有一個Sequence Number(你可以認為是一個提案號,這個數不斷遞增,而且是唯一的,也就是說A和B不可能有相同的提案號),這個提案號會和修改請求一同發出,任何結點在“Prepare階段”時都會拒絕其值小於當前提案號的請求。所以,結點A在向所有結點申請修改請求的時候,需要帶一個提案號,越新的提案,這個提案號就越是是最大的。
如果接收結點收到的提案號n大於其它結點發過來的提案號,這個結點會回應Yes(本結點上最新的被批準提案號),並保證不接收其它<n的提案。這樣一來,結點上在Prepare階段裏總是會對最新的提案做承諾。
優化:在上述 prepare 過程中,如果任何一個結點發現存在一個更高編號的提案,則需要通知 提案人,提醒其中斷這次提案。
第二階段:Accept階段
如果提案者A收到了超過半數的結點返回的Yes,然後他就會向所有的結點發布Accept Request(同樣,需要帶上提案號n),如果沒有超過半數的話,那就返回失敗。
當結點們收到了Accept Request後,如果對於接收的結點來說,n是最大的了,那麽,它就會修改這個值,如果發現自己有一個更大的提案號,那麽,結點就會拒絕修改。
我們可以看以,這似乎就是一個“兩段提交”的優化。其實,2PC/3PC都是分布式一致性算法的殘次版本,Google Chubby的作者Mike Burrows說過這個世界上只有一種一致性算法,那就是Paxos,其它的算法都是殘次品。
我們還可以看到:對於同一個值的在不同結點的修改提案就算是在接收方被亂序收到也是沒有問題的。
關於一些實例,你可以看一下Wikipedia中文中的“Paxos樣例”一節,我在這裏就不再多說了。對於Paxos算法中的一些異常示例,大家可以自己推導一下。你會發現基本上來說只要保證有半數以上的結點存活,就沒有什麽問題。
多說一下,自從Lamport在1998年發表Paxos算法後,對Paxos的各種改進工作就從未停止,其中動作最大的莫過於2005年發表的Fast Paxos。無論何種改進,其重點依然是在消息延遲與性能、吞吐量之間作出各種權衡。為了容易地從概念上區分二者,稱前者Classic Paxos,改進後的後者為Fast Paxos。
總結
下圖來自:Google App Engine的co-founder Ryan Barrett在2009年的google i/o上的演講《Transaction Across DataCenter》(視頻: http://www.youtube.com/watch?v=srOgpXECblk)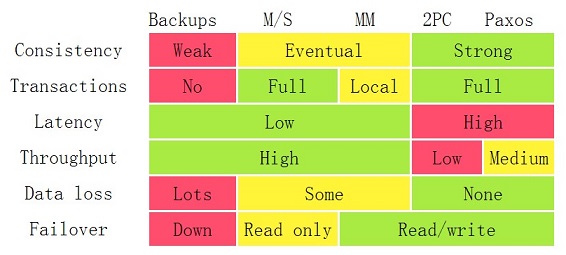
前面,我們說過,要想讓數據有高可用性,就需要冗余數據寫多份。寫多份的問題會帶來一致性的問題,而一致性的問題又會帶來性能問題。從上圖我們可以看到,我們基本上來說不可以讓所有的項都綠起來,這就是著名的CAP理論:一致性,可用性,分區容忍性,你只可能要其中的兩個。
NWR模型
最後我還想提一下Amazon Dynamo的NWR模型。這個NWR模型把CAP的選擇權交給了用戶,讓用戶自己的選擇你的CAP中的哪兩個。
所謂NWR模型。N代表N個備份,W代表要寫入至少W份才認為成功,R表示至少讀取R個備份。配置的時候要求W+R > N。 因為W+R > N, 所以 R > N-W 這個是什麽意思呢?就是讀取的份數一定要比總備份數減去確保寫成功的倍數的差值要大。
也就是說,每次讀取,都至少讀取到一個最新的版本。從而不會讀到一份舊數據。當我們需要高可寫的環境的時候,我們可以配置W = 1 如果N=3 那麽R = 3。 這個時候只要寫任何節點成功就認為成功,但是讀的時候必須從所有的節點都讀出數據。如果我們要求讀的高效率,我們可以配置 W=N R=1。這個時候任何一個節點讀成功就認為成功,但是寫的時候必須寫所有三個節點成功才認為成功。
NWR模型的一些設置會造成臟數據的問題,因為這很明顯不是像Paxos一樣是一個強一致的東西,所以,可能每次的讀寫操作都不在同一個結點上,於是會出現一些結點上的數據並不是最新版本,但卻進行了最新的操作。
所以,Amazon Dynamo引了數據版本的設計。也就是說,如果你讀出來數據的版本是v1,當你計算完成後要回填數據後,卻發現數據的版本號已經被人更新成了v2,那麽服務器就會拒絕你。版本這個事就像“樂觀鎖”一樣。
但是,對於分布式和NWR模型來說,版本也會有惡夢的時候——就是版本沖的問題,比如:我們設置了N=3 W=1,如果A結點上接受了一個值,版本由v1 -> v2,但還沒有來得及同步到結點B上(異步的,應該W=1,寫一份就算成功),B結點上還是v1版本,此時,B結點接到寫請求,按道理來說,他需要拒絕掉,但是他一方面並不知道別的結點已經被更新到v2,另一方面他也無法拒絕,因為W=1,所以寫一分就成功了。於是,出現了嚴重的版本沖突。
Amazon的Dynamo把版本沖突這個問題巧妙地回避掉了——版本沖這個事交給用戶自己來處理。
於是,Dynamo引入了Vector Clock(矢量鐘?!)這個設計。這個設計讓每個結點各自記錄自己的版本信息,也就是說,對於同一個數據,需要記錄兩個事:1)誰更新的我,2)我的版本號是什麽。
下面,我們來看一個操作序列:
1)一個寫請求,第一次被節點A處理了。節點A會增加一個版本信息(A,1)。我們把這個時候的數據記做D1(A,1)。 然後另外一個對同樣key的請求還是被A處理了於是有D2(A,2)。這個時候,D2是可以覆蓋D1的,不會有沖突產生。
2)現在我們假設D2傳播到了所有節點(B和C),B和C收到的數據不是從客戶產生的,而是別人復制給他們的,所以他們不產生新的版本信息,所以現在B和C所持有的數據還是D2(A,2)。於是A,B,C上的數據及其版本號都是一樣的。
3)如果我們有一個新的寫請求到了B結點上,於是B結點生成數據D3(A,2; B,1),意思是:數據D全局版本號為3,A升了兩新,B升了一次。這不就是所謂的代碼版本的log麽?
4)如果D3沒有傳播到C的時候又一個請求被C處理了,於是,以C結點上的數據是D4(A,2; C,1)。
5)好,最精彩的事情來了:如果這個時候來了一個讀請求,我們要記得,我們的W=1 那麽R=N=3,所以R會從所有三個節點上讀,此時,他會讀到三個版本:
- A結點:D2(A,2)
- B結點:D3(A,2; B,1);
- C結點:D4(A,2; C,1)
6)這個時候可以判斷出,D2已經是舊版本(已經包含在D3/D4中),可以舍棄。
7)但是D3和D4是明顯的版本沖突。於是,交給調用方自己去做版本沖突處理。就像源代碼版本管理一樣。
很明顯,上述的Dynamo的配置用的是CAP裏的A和P。
我非常推大家都去看看這篇論文:《Dynamo:Amazon’s Highly Available Key-Value Store》,如果英文痛苦,你可以看看譯文(譯者不詳)。
原文鏈接:http://coolshell.cn/articles/10910.html
分布式系統的事務處理
