chunlvxiong的博客

題目描述：

　　有N(1≤N≤1000)件產品，每個產品生產需要操作A和操作B。有M1(1≤M1≤30)件機器完成操作A，M2(1≤M2≤30)件機器完成操作B，分別給出每臺機器完成相應操作的時間。產品必須先進行操作A再進行操作B，問：所有產品完成操作A的時間和所有產品完成操作B的時間是多少。

思考&分析：

　　第一問比較好解決，可以貪心處理。假設第i臺機器加工了xi件產品，那麽所有產品完成操作A的時間就是max{xi*time_a[i]}。由於每次必須有一個xi+1，那麽你的貪心策略就是讓(xi+1)*time_a[i]最小（也就是讓這次的產品完成時間最小）。這裏你可以使用堆來維護(xi+1)*time_a[i]（詳見代碼），同時你每次也可以算出每個產品完成操作A的時間（是一個非遞減序列）。

　　第二問很明顯要借用第一問的計算結果（每個產品的完成時間）。設產品i完成操作A的時間是ti，然後我們考慮：

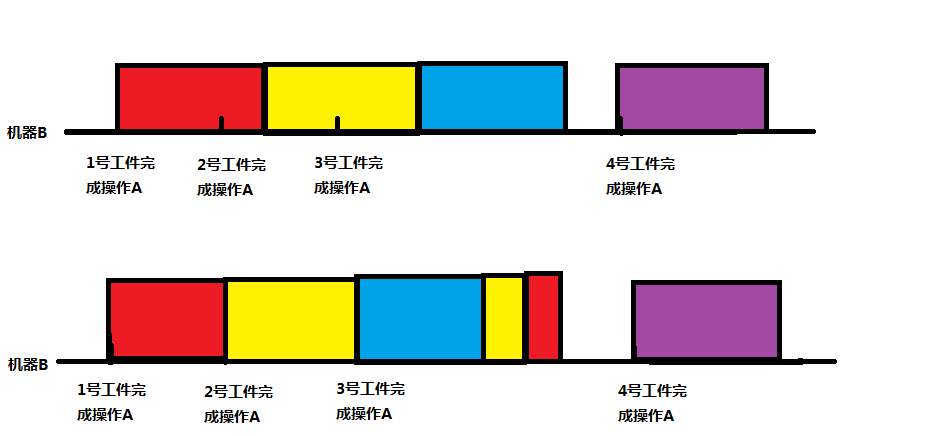
　　這兩個圖是說：交換時間段對於問題的答案無影響。-->這有什麽用呢？例如：忽略4號工件，那麽3號工件結束時間是t[3]+time_b，2號工件結束時間是t[2]+time_b*2，1號工件結束時間為t[1]+time_b*3-->一個簡單想法：對於完成操作A的時間第i靠後的工件x，其結束時間為t[x]+time_b*i。

　　那麽如果加入了4號工件呢？三號工件的完成時間變成了t[3]+time_b*2，然而實際上它的完成時間是t[3]*time_b-->但是這並沒有關系，因為t[3]+time_b*2不可能超過t[4]+time_b，不影響最大值（如果t[3]+time_b*2大於t[4]+time_b說明最大時間是t[3]+time_b*2）。也就是說，剛才那個簡單想法是行的通的。

　　這樣問題就變得容易很多：貪心策略可以為每次讓最後完成操作A的工件放到(xi+1)*time_b[i]最小的機器上（由於其t值大，所以要減小這個值以避免max過大）。那麽這個維護又變成了第一問的堆維護，但要註意這次的序列不在具有非遞減的性質，需要取max來獲得ans。

　　總時間復雜度O(NlogM)。

貼代碼：

#include <bits/stdc++.h>
using namespace std;
int n,m1,m2,a[35],b[35],end_a[1005];
struct node{
    int x,y;
    friend bool operator <(node a,node b){
        
 
return a.x>b.x;
    }
};
priority_queue<node>Q;
void solve1(){
    sort(a+1,a+m1+1);
    for (int i=1;i<=m1;i++)
        Q.push(node{a[i],i});
    for (int i=1,x,y;i<=n;i++){
        x=Q.top().x,y=Q.top().y;
        Q.pop();
        end_a[i]=x;
        Q.push(node{x+a[y],y});
    }
    printf("%d ",end_a[n]);
    while (!Q.empty()) Q.pop();
}
void solve2(){
    sort(b+1,b+m2+1);
    for (int i=1;i<=m2;i++)
        Q.push(node{b[i],i});
    int ans=0;
    for (int i=n,x,y;i>=1;i--){
        x=Q.top().x,y=Q.top().y;
        Q.pop();
        ans=max(ans,end_a[i]+x);
        Q.push(node{x+b[y],y});
    }
    printf("%d\n",ans);
}
int main(){
    freopen("job.in","r",stdin);
    freopen("job.out","w",stdout);
    scanf("%d%d%d",&n,&m1,&m2);
    for (int i=1;i<=m1;i++) scanf("%d",&a[i]);
    for (int i=1;i<=m2;i++) scanf("%d",&b[i]);
    solve1();
    solve2();
    return 0;
}

USACO4.2.3-Job Processing