VIO回顧：從濾波和優化的視角
https://mp.weixin.qq.com/s/zpZERtWPKljWNAiASBLJxA
根據以上網頁自己做的總結：
在機器人社區中，定位與構圖問題屬於狀態估計問題。主流使用的工具可以對給定噪聲測量的動態系統進行隨機估計，例如擴展卡爾曼濾波器（EKF）或粒子濾波器（PF）。 一些內部傳感器可以測量姿勢隨時間的變化，這種變化關系可以用公式表示為移動平臺的數據驅動動力學模型，包括地面移動機器人中的光學編碼器和飛行機器人中的IMU，眾所周知它們具有累積誤差和測量偏差。 一些外部傳感器，如相機或激光測距儀，能夠提供角度或距離測量。基於三角測量或三邊測量方法，這些傳感器能夠估計位置移動平臺的位置和方向。 估計結果的可靠性在很大程度上取決於環境條件，而且結果對測量噪聲敏感。 然而，在狀態估計問題中，它們可以用測量模型來公式化表示。於是，EKF或PF能夠通過融合動態模型中的分布和測量模型中的分布來推得從上一步到當前的估計分布。在大多數情況下，由於被估計狀態數量過多，人們會用PF代替EKF，然後估計出高斯分布的均值和協方差。
在計算機視覺領域，由視覺進行運動估計是一個優化問題[5]。通過圖像配準的叠代計算求得變化的相機姿態[6,7]。通常，從一幅圖像中提取特征並重新投影到另一幅不同視角的圖像中（重投影），這樣，最小化特征與重投影特征的誤差代價，就可以解算出相機相對結構化環境的姿態變化。基於優化的算法主要是基於梯度的，例如牛頓法或高斯-牛頓法。 多數情況下，我們可以利用矩陣的稀疏結構來提升計算效率。 優化的結果僅提供估計狀態的值，而估計分布的信息是不可用的。
利用貝葉斯推理框架可以建立基於濾波和基於優化兩種方法之間的聯系。基於優化的方法，叠代地找到測量的總概率最高的狀態，故可被看作為最大似然
流行的SLAM技術能估計平臺姿態和環境結構。需要通過閉環檢測的過程來約束由估計算法引起的累積誤差。然而，在VIO技術中沒有明確地要求閉環檢測[8-10]。 因此，VIO中的估計誤差將被累積並且不能被約束。由於沒有閉環檢測，在小尺寸的裝置內就可以進行長時間和大規模的定位。因此，研究重心也就轉向了如何開發可以減慢誤差累積的技術。
基於濾波的方法
EKF框架通常由預測步驟和更新步驟組成。對於基於濾波的VIO方法，慣性傳感器測量得到的三軸加速度和轉動速度，可用於計算3D剛體運動的數據驅動動力學模型或先驗分布，並且可在預測步驟中用來進行運動預測。相機能夠提供特征和移動平臺之間的角度和距離測量，可用作測量模型或似然分布，並用於在更新步驟中更新預測。
我們假設這樣一個移動平臺，只配備一個相機和一個IMU，在未知的環境中移動。相機和IMU之間的空間關系是固定的，而且可以用已知的位姿表示。基於EKF的VIO算法的目的是使用慣性測量和對未知環境的視覺觀測來提供平臺的位置和方向信息。接下來，我們將基於[11]中的工作給出EKF框架的完整描述，包括狀態描述，IMU數據驅動動力學和視覺觀測。
2.1. IMU數據驅動動力學模型
任意時刻的3D剛體的IMU狀態向量可以由16×1向量定義：
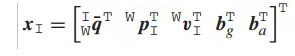
其中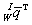
是單位四元數，用來描述從世界幀{W}到IMU幀{I}的旋轉。
和
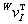是關於{W}的位置和速度，
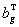和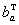
是3×1向量，分別用來描述影響陀螺儀和加速度計測量的偏差。幀間的空間關系如圖1所示。
2.2 誤差狀態表示與更新
2.3 視覺測量模型與更新
由於IMU數據中存在偏差和噪聲，預測步驟的預測結果會隨著時間的增加而變得越來越差。視覺傳感器的測量恰好能夠提供關鍵信息以限制誤差的增加。為了在EKF框架中用這方法，從圖像中提取的關鍵信息要被轉換成測量方程。有各種方法來構建測量模型。例如，松耦合方法中，通過圖像配準直接獲得位置和方向的變化，然後在EKF框架中融合兩者估計結果。[13]而所謂的緊耦合方法則提倡使用從圖像提取的關鍵信息。關鍵信息可以是通過特征檢測器從圖像中特征提取得到[14]，也可以由具有深度信息（點雲）的直接光強度[15,16]與半直接光強度得到。[17]需要分析關鍵信息和狀態變量之間的關系，使其建模為測量方程。
完整的更新過程總結如下：
（a）對於特定采樣頻率中的視覺數據，通常在原始圖像上采用一些圖像處理程序來提取關鍵信息。
（b）計算殘差（7）。
（c）計算卡爾曼增益（8）。
（d）通過添加修正來更新狀態。
（e）更新誤差狀態協方差矩陣（9）。
. 基於優化的方法
基於優化的方法主要依賴於特征提取的圖像處理技術和圖像配準的最優化，而慣性測量被視為先驗，可當作正則項或完全忽略。在大多數情況下，基於優化的方法有兩個階段：構圖和跟蹤。[15]在構圖階段，由各種特征檢測器從圖像中提取特征，如3D空間中的角點，邊緣或其他地標。然後，對於檢測到的所有特征，定義兩幀圖像之間的重投影誤差。該誤差用作要優化的損失函數，以便找到特征或地標的坐標。[7]在跟蹤階段中，地圖中特征和地標的坐標被用於定義兩幀圖像之間的重投影誤差，並且再次應用優化算法以計算出移動平臺的位置和方向的變化。將估計問題分為兩個階段的想法可以獲得快速的跟蹤結果，然而構圖處理還是耗時的。[14,15]對於上述分別由3D特征的坐標和移動平臺的姿態改變定義的兩個重投影誤差損失函數，同時優化是可能的。[19]引入關鍵幀的概念能夠邊緣化舊的狀態而保持一個有界優化窗口，保證實時性。
3.1 特征配準
叠代非線性優化可以通過最小化圖像觀測區域的重投影誤差來找到相機姿態改變和/或特征坐標。通常，地圖由多個關鍵幀中標識的特征組成，即一系列的3D坐標向量表示，其中關鍵幀中包含著顯著的特征。當獲得新的圖像時，應當判斷其是否是關鍵幀。如果是，則將該新圖像中通過圖像配準算法計算找到的新特征坐標與當前相機姿態一起添加到地圖中。否則，地圖不更新。
圖像配準中優化的目的是在每個時間步長中找到變換T，即T被認為是相機姿態。用局部最小的形式表示相機姿態更適合用於優化。
3.2 稠密配準
在上述討論中，使用圖像的特征或地標的坐標來定義重投影誤差。然而，它需要特征檢測過程，由於特征被稀疏地提取，導致圖像中的大部分信息被忽略了。特征提取過程通常存在噪聲和不魯棒等糟糕的問題，因此需要有更高水平的魯棒估計技術。由於所有這些估計步驟都不在原始圖像測量（強度）層級，它們會徹底地傳播特征提取誤差和累積漂移。
另一方面，基於表觀和光流的技術是基於圖像的，並且直接基於原始圖像的測量[21]做最小化誤差，即使用光度（亮度或強度）函數，因此被稱為直接或稠密方法。稠密方法旨在使用整幅圖像進行配準。非線性優化技術用於找到兩個場景之間的變換關系。我們越來越清楚，使用稠密的方法用於構圖和跟蹤可以獲得更加完整，準確和魯棒的結果。文[22,23]中的工作通過使用Kinect RGB-D相機做視覺裏程計，通過最小化光度誤差實現圖像配準。文[24]中的工作包括最小化光度誤差和深度誤差。
使用RGB-D相機（例如Kinect傳感器），像素的深度信息通過最小化每幅圖像中的所有數據間的距離測量實現多個掃描的配準，而不是有限數量的特征或地標。這種稠密掃描能夠重建環境中的場景表面並跟蹤姿態。給定兩個連續的稠密深度測量，從不同視角觀察到的同一靜態場景的表面或3D點雲，一個點雲映射到另一個上的最佳剛體變換對應了相機的姿態變化。
叠代最近點（ICP）是通過優化剛體變換來匹配掃描的流行算法。[25]ICP工作方式如下：給定兩個對應點集：β= {β1，...，βn}和γ= {γ1，...，γn}，它們之間的平移和旋轉分別為t和R，t和R可以通過最小化誤差平方和得到：
如果正確的對應關系已知，則計算旋轉和平移是有閉合解的。然而在大多數情況下，正確的對應關系是未知的，則通常不能一步求解出相應的最佳旋轉和平移。通過找到最近點的對應關系，以叠代的方式進行配準。[25]如果初始位置足夠接近，ICP算法會收斂。在文[26]中報道了使用ICP進行視覺裏程計的一項工作。
稠密配準也可以通過將當前圖像與場景模型匹配來進行。KinectFusion方法為稠密配準提供了實時的解決方案，[27]其在GPU中將構圖和跟蹤線程分離，並用截斷符號距離函數構建場景模型。然而，對整個點雲執行ICP算法的計算代價是昂貴的，並且在通用PC上不能提供實時解決方案。
對於單目相機，深度信息未知。在構圖線程中通過非凸優化算法求解最小化光度誤差來估計反向深度圖。[15]在跟蹤線程中，使用圖像配準。在單目相機中也通過貝葉斯濾波器估計深度信息，隨後用優化過程平滑得到的深度圖[28]。
為了進一步簡化計算復雜度並保持稠密方法的準確性，近年來人們提出了一些半稠密或半直接方法。[29,30]半密集深度圖覆蓋了整個圖像區域，也包括重要的梯度信息。使用貝葉斯濾波器來估計反向深度圖，同時通過直接最小化稠密光度誤差來實現跟蹤。如文[30]中所述，半直接或半稠密方法使用數百個小塊來增加魯棒性，並允許忽略塊的法向量。
3.3 慣性測量項
在基於濾波的方法中，IMU傳感器的測量作為數據驅動3D剛體運動動力學的數據源，並且通過卡爾曼濾波器與相機的測量融合。這類是緊耦合的，算法中考慮了兩者的互協方差。[11]而松耦合融合方式是以定常時間，將IMU得到的預測姿態和視覺傳感器的已估計姿態在EKF框架中融合。[31]在基於優化的方法中，也可以將兩部分緊密融合，即不需要來自相機的顯式姿態估計。IMU驅動動力學方程（1）中的預測結果是高斯分布。預測結果和真實狀態之間的誤差被投射為由協方差加權的平方誤差，然後作為正則化項加到損失函數中。[19]根據貝葉斯推理，正則化項被視為先驗，而圖像配準項被視為似然性。優化結果是後驗分布，由純圖像配準的ML估計結果得到，然後IMU先驗對這個估計結果進行平滑。
4.濾波方法與優化方法的聯系
基於濾波和基於優化的方法都可以在貝葉斯推理下形成。經由近似線性化，兩者的聯系可以通過叠代EKF來明確表示。當近似線性化僅是單個步驟時，包含前通和後通的基於平滑的方法，等價於利用最小二乘問題中信息矩陣的Cholesky分解來求解的基於優化的方法。為了降低計算復雜度，通過保留僅有的關鍵幀或滑動窗口來減少要估計的狀態變量。特別地，滑動窗的方案或滾動時域估計將損失函數劃分為兩部分，流行的方式是在一個部分中優化結果，在另一部分中用EKF來忽視過去的狀態。
4.1 叠代EKF更新
基於濾波的方法核心是卡爾曼濾波器，而基於優化的方法核心是高斯-牛頓方法。它們之間可以通過叠代EKF（IEKF）[32]來聯系。EKF有兩個步驟：預測和更新。假設當前時刻k預測步驟的結果為
EKF和IEKF之間的區別在於，在IEKF的更新步驟中存在叠代循環，而在EKF的更新步驟中只執行單個循環。IEKF的叠代循環能使由模型線性化導致的誤差盡可能接近基於優化的方法中的結果。接下來，我們將說明IEKF更新步驟中的叠代循環與基於最大化似然（ML）優化方法的高斯-牛頓方法兩者是如何等價的。
4.2 基於平滑的方法
基於濾波的方法是序列叠代的過程，當前估計結果取決於當前測量和過去的估計結果（過去測量被精簡在過去的估計結果中），即未來測量不對當前估計結果做任何貢獻。反之，若未來的測量確實對當前估計結果做貢獻，則屬於應用了基於平滑的方法。這更像是一種批處理算法，所有測量都可用於估計。[33]
4.3 邊緣化到關鍵幀
若如上述情形這樣，保持操作過程中所有的狀態變量和特征交會，那麽隨著探索軌跡的增加，計算復雜度會變得越來越大。然而，不是所有的傳感器數據都是有用的。其中一些包含了關於跟蹤和構圖的關鍵信息，而另一些則是冗余的或不重要的信息可被忽略。有兩種方法從過去的歷史數據中選取有用的信息。一種是固定窗口方案，其僅保留最近的N個數據測量，而將N個測量之前的所有數據簡單地邊緣化。另一個是如圖4所示，根據一些標準從整個數據集中選擇N個數據測量。通過數據中的決定性信息來篩選關鍵幀是最普及的標準，在整個算法處理期間保留這些關鍵幀即可。[19,34]
4.3 滾動時域估計
滾動時域估計（MHE）方法將MAP損失函數分為兩部分。如圖4所示，在每個步驟中，只有從k步到步的最近N個項被優化，而最舊的項由EKF近似被概括為到達代價。
假設時間間隔為[0，k-N]和。 MAP問題是
前N項和是到達代價，MHE問題就是
其中是MHE窗口的開始時間，
是在
時刻的到達代價。到達代價由EKF近似為：
其中協方差P傳播方式如下
VIO回顧：從濾波和優化的視角