蒟蒻居然今天第一次寫網絡流 我太弱啦！

最大流問題有很多解法 雖然isap常數巨小 但是連dinic都寫掛的本蒟蒻並不會orz

那麽我們選用比較好實現的dinic來解決最大流問題

來一段定義：

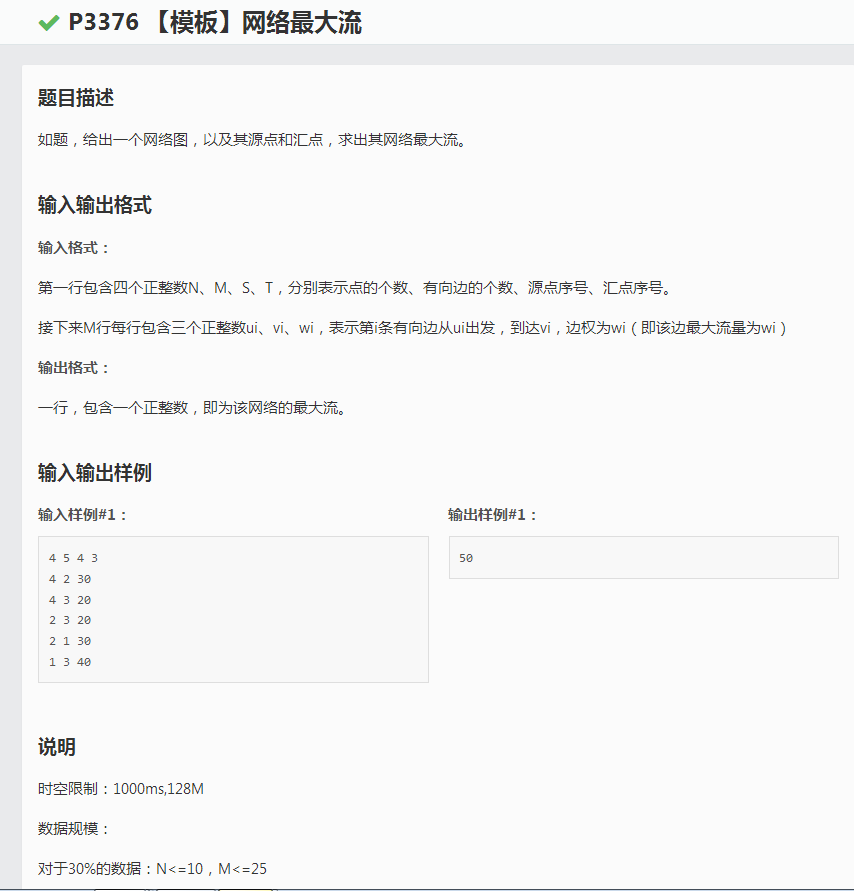
於是我們就可以這樣實現啦！

#pragma GCC optimize("O2")
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<limits.h>
#include<ctime>
#define N 100001
typedef long long ll;
const int inf=0x3fffffff;
const int maxn=2017;
using namespace std;
inline int read()
{
    int f=1,x=0;char ch=getchar();
    while(ch>‘9‘||ch<‘0‘)
    {
        if(ch==‘-‘)
        f=-1;
        ch=getchar();
    }
    while(ch<=‘9‘&&ch>=‘0‘)
    {
        x=(x<<3)+(x<<1)+ch-‘0‘;
        ch=getchar();
    }
    return f*x;
}
struct tsdl{
	int w,to,next;
} edge[N*4];
int dis[N],head[N],q[N],tot,astart,aend;
void add(int ui,int vi,int wi)
{
	edge[tot].next=head[ui];
	edge[tot].w=wi;
	edge[tot].to=vi; 
    head[ui]=tot++;
}
int m,n;
bool bfs()
{
	queue<int>q;
	memset(dis,0,sizeof(dis));
	dis[astart]=1;
	q.push(astart);
	while(!q.empty())
	{
		int x=q.front();
		q.pop();
		for(int i=head[x];i!=-1;i=edge[i].next)
		{
			if(edge[i].w&&!dis[edge[i].to])
			{
				dis[edge[i].to]=dis[x]+1;
				q.push(edge[i].to);
			}
		}
	} 
	if(dis[aend])return 1;
	return 0;
}
int dfs(int u,int lim)
{
	if(u==aend||!lim)return lim;
	int ret=0;
	for(int i=head[u];i!=-1;i=edge[i].next)
	{
		if(dis[edge[i].to]==dis[u]+1)
		{
			int f=dfs(edge[i].to,min(edge[i].w,lim));
			edge[i].w-=f;
			edge[i^1].w+=f;
			lim-=f,ret+=f;
		}
	}
	if(!ret)dis[u]=-1;
	return ret;
}
int main()
{
	memset(head,-1,sizeof(head));
	int ans=0;
	n=read(),m=read(),astart=read(),aend=read();
	for(int i=1;i<=m;i++)
	{
		int u=read(),v=read(),w=read();
		add(u,v,w);
		add(v,u,0);
	}
	while(bfs())ans+=dfs(astart,inf);
	printf("%d\n",ans);
}

註意反向邊權值為0，以及鄰接表需要從0開始以保證反向邊的對應關系

最大流：Dinic算法