根據前序遍歷和中序遍歷求後序遍歷

一道HULU的筆試題(How I wish yesterday once more)

假設有棵樹，長下面這個樣子，它的前序遍歷，中序遍歷，後續遍歷都很容易知道。

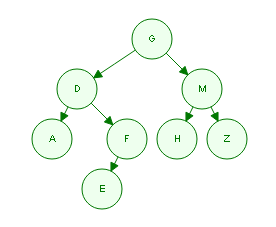
PreOrder: GDAFEMHZ

InOrder: ADEFGHMZ

PostOrder: AEFDHZMG

現在，假設僅僅知道前序和中序遍歷，如何求後序遍歷呢？比如，已知一棵樹的前序遍歷是”GDAFEMHZ”，而中序遍歷是”ADEFGHMZ”應該如何求後續遍歷?

第一步，root最簡單，前序遍歷的第一節點G就是root。

第二步，繼續觀察前序遍歷GDAFEMHZ，除了知道G是root，剩下的節點必然是root的左右子樹之外，沒法找到更多信息了。

第三步，那就觀察中序遍歷ADEFGHMZ。其中root節點G左側的ADEF必然是root的左子樹，G右側的HMZ必然是root的右子樹。

第四步，觀察左子樹ADEF，左子樹的中的根節點必然是大樹的root的leftchild。在前序遍歷中，大樹的root的leftchild位於root之後，所以左子樹的根節點為D。

第五步，同樣的道理，root的右子樹節點HMZ中的根節點也可以通過前序遍歷求得。在前序遍歷中，一定是先把root和root的所有左子樹節點遍歷完之後才會遍歷右子樹，並且遍歷的右子樹的第一個節點就是右子樹的根節點。

如何知道哪裏是前序遍歷中的左子樹和右子樹的分界線呢？通過中序遍歷去數節點的個數。

在上一次中序遍歷中，root左側是A、D、E、F，所以有4個節點位於root左側。那麽在前序遍歷中，必然是第1個是G，第2到第5個由A、D、E、F過程，第6個就是root的右子樹的根節點了，是M。

第六步，觀察發現，上面的過程是遞歸的。先找到當前樹的根節點，然後劃分為左子樹，右子樹，然後進入左子樹重復上面的過程，然後進入右子樹重復上面的過程。最後就可以還原一棵樹了。

第七步，其實，如果僅僅要求寫後續遍歷，甚至不要專門占用空間保存還原後的樹。只需要稍微改動第六步，就能實現要求。僅需要把第六步的遞歸的過程改動為如下:

1 確定根,確定左子樹，確定右子樹。

2 在左子樹中遞歸。

3 在右子樹中遞歸。

4 打印當前根。

參考了一些網上的討論，具體程序是:

#include <iostream>  
#include <fstream>  
#include <string>  
  
struct TreeNode  
{  
  struct TreeNode* left;  
  struct TreeNode* right;  
  char  elem;  
};  
  
  
TreeNode* BinaryTreeFromOrderings(char* inorder, char* preorder, int length)  
{  
  if(length == 0)  
    {  
      return NULL;  
    }  
  TreeNode* node = new TreeNode;//Noice that [new] should be written out.  
  node->elem = *preorder;  
  int rootIndex = 0;  
  for(;rootIndex < length; rootIndex++)//a variation of the loop  
    {  
      if(inorder[rootIndex] == *preorder)  
      break;  
    }  
  node->left = BinaryTreeFromOrderings(inorder, preorder +1, rootIndex);  
  node->right = BinaryTreeFromOrderings(inorder + rootIndex + 1, preorder + rootIndex + 1, length - (rootIndex + 1));  
  std::cout<<node->elem<<std::endl;  
  return node;  
}  
  
int main(int argc, char** argv){  
    char* pr="GDAFEMHZ";      
 char* in="ADEFGHMZ"; BinaryTreeFromOrderings(in, pr, 8); printf("\n"); return 0;}

根據前序遍歷和中序遍歷求後序遍歷