一、貝葉斯定理數學基礎

　　我們都知道條件概率的數學公式形式為

　　即B發生的條件下A發生的概率等於A和B同時發生的概率除以B發生的概率。

　　根據此公式變換，得到貝葉斯公式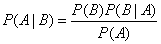： 即貝葉斯定律是關於隨機事件A和B的條件概率（或邊緣概率）的一則定律。通常，事件A在事件B發生的條件溪的概率，與事件B在事件A的條件下的概率是不一樣的，而貝葉斯定律就是描述二者之間的關系的。

　　更進一步將貝葉斯公式進行推廣，假設事件A發生的概率是由一系列的因素(A1,A2,A3,...An)決定的，則事件A的全概率公式為：

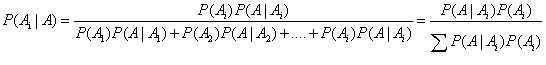
　　二、樸素貝葉斯分類

　　樸素貝葉斯分類是一種十分簡單的分類算法，其思想基礎是：對於給定的待分類項，求解在此項出現的條件下各個類別出現的概率，哪個最大，就認為此待分類項就屬於哪個類別。

　　假設V=(v1,v2,v3....vn)是一個待分項，而vn為V的每個特征向量；

　　 B=(b1,b2,b3...bn)是一個分類集合，bn為每個具體的分類；

　　　　如果需要測試某個Vn歸屬於B集合中的哪個具體分類，則需要計算P(bn|V)，即在V發生的條件下，歸屬於b1,b2,b3,....bn中哪個可能性最大。即：

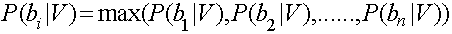
　　　　因此，這個問題轉換成求每個待分項分配到集合中具體分類的概率是多少。而這個·具體概率的求法可以使用貝葉斯定律。

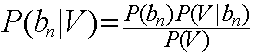
　　　　經過變換得出：

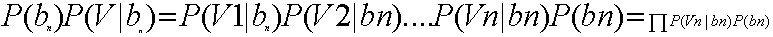
　　三、MLlib對應的API

　　1、貝葉斯分類伴生對象NativeBayes,原型：

object NaiveBayes extends scala.AnyRef with scala.Serializable {
  def train(input : org.apache.spark.rdd.RDD[org.apache.spark.mllib.regression.LabeledPoint]) : org.apache.spark.mllib.classification.NaiveBayesModel = { /* compiled code */ }
  def train(input : org.apache.spark.rdd.RDD[org.apache.spark.mllib.regression.LabeledPoint], lambda : scala.Double) : org.apache.spark.mllib.classification.NaiveBayesModel = { /* compiled code */ }
}

　　其主要定義了訓練貝葉斯分類模型的train方法，其中input為訓練樣本，lambda為平滑因子參數。

　　2、train方法，其是NativeBayes對象的靜態方法，根據設置的樸素貝葉斯分類參數新建樸素貝葉斯分類類，並執行run方法進行訓練。

　　3、樸素貝葉斯分類類NaiveBayes,原型：

class NaiveBayes private (private var lambda : scala.Double) extends scala.AnyRef with scala.Serializable with org.apache.spark.Logging {
  def this() = { /* compiled code */ }
  def setLambda(lambda : scala.Double) : org.apache.spark.mllib.classification.NaiveBayes = { /* compiled code */ }
  def run(data : org.apache.spark.rdd.RDD[org.apache.spark.mllib.regression.LabeledPoint]) : org.apache.spark.mllib.classification.NaiveBayesModel = { /* compiled code */ }
}

　　4、run方法，該方法主要計算先驗概率和條件概率。首先對所有樣本數據進行聚合，以label為key，聚合同一個label的特征features，得到所有label的統計(label，features之和),然後根據label統計數據，再計算p(i),和theta(i)(j)，最後，根據類別標簽列表、類別先驗概率、各類別下的每個特征的條件概率生成貝葉斯模型。

　　先驗概率並取對數p(i)=log(p(yi))=log((i類別的次數+平滑因子)/(總次數+類別數*平滑因子)）)

　　各個特征屬性的條件概率，並取對數

　　theta(i)(j)=log(p(ai|yi))=log(sumTermFreqs(j)+平滑因子)-thetaLogDenom

　　其中，theta(i)(j)是類別i下特征j的概率，sumTermFreqs(j)是特征j出現的次數，thetaLogDenom一般分2種情況，如下：

　　　　1.多項式模型

　　　　　　thetaLogDenom=log(sumTermFreqs.values.sum+ numFeatures* lambda)

　　　　　　其中，sumTermFreqs.values.sum類別i的總數，numFeatures特征數量，lambda平滑因子

　　　　2.伯努利模型

　　　　　　thetaLogDenom=log(n+2.0*lambda)

　　5、aggregated:對所有樣本進行聚合統計，統計沒個類別下的每個特征值之和及次數。

　　6、pi表示各類別·的·先驗概率取自然對數的值

　　7、theta表示各個特征在各個類別中的條件概率值

　　8、predict:根據模型的先驗概率、條件概率，計算樣本屬於每個類別的概率，取最大項作為樣本的類別

　　9、貝葉斯分類模型NaiveBayesModel包含參數：類別標簽列表(labels)、類別先驗概率(pi)、各個特征在各個類別中的條件概率(theta)。

　　四、使用示例

　　1、樣本數據:

0,1 0 0
0,2 0 0
1,0 1 0
1,0 2 0
2,0 0 1
2,0 0 2

import org.apache.spark.mllib.classification.NaiveBayes
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.util.MLUtils
import org.apache.spark.{SparkConf, SparkContext}

object Bayes {
  def main(args: Array[String]): Unit = {
    val conf=new SparkConf().setAppName("BayesDemo").setMaster("local")
    val sc=new SparkContext(conf)
    //讀取樣本數據，此處使用自帶的處理數據方式·
    val data=MLUtils.loadLabeledPoints(sc,"d://bayes.txt")
    //訓練貝葉斯模型
    val model=NaiveBayes.train(data,1.0)
    //model.labels.foreach(println)
    //model.pi.foreach(println)
    val test=Vectors.dense(0,0,100)
    val res=model.predict(test)
    println(res)//輸出結果為2.0
  }
}

import org.apache.log4j.{Level, Logger}
import org.apache.spark.mllib.classification.NaiveBayes
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.regression.LabeledPoint
import org.apache.spark.{SparkConf, SparkContext}

object Bayes {
  def main(args: Array[String]): Unit = {
    //創建spark對象
    val conf=new SparkConf().setAppName("BayesDemo").setMaster("local")
    val sc=new SparkContext(conf)
    Logger.getRootLogger.setLevel(Level.WARN)
    //讀取樣本數據
    val data=sc.textFile("d://bayes.txt")//讀取數據
    val demo=data.map{ line=>//處理數據
      val parts=line.split(‘,‘)//分割數據·
      LabeledPoint(parts(0).toDouble,//標簽數據轉換
        Vectors.dense(parts(1).split(‘ ‘).map(_.toDouble)))//向量數據轉換
    }
    //將樣本數據分為訓練樣本和測試樣本
    val sp=demo.randomSplit(Array(0.6,0.4),seed = 11L)//對數據進行分配
    val train=sp(0)//訓練數據
    val testing=sp(1)//測試數據
    //建立貝葉斯分類模型，並進行訓練
    val model=NaiveBayes.train(train,lambda = 1.0)

    //對測試樣本進行測試
    val pre=testing.map(p=>(model.predict(p.features),p.label))//驗證模型
    val prin=pre.take(20)
    println("prediction"+"\t"+"label")
    for(i<- 0 to prin.length-1){
      println(prin(i)._1+"\t"+prin(i)._2)
    }
　　　　val accuracy=1.0 *pre.filter(x=>x._1==x._2).count()//計算準確度

println(accuracy)

}
 }

Spark 貝葉斯分類算法