凸多邊形分割

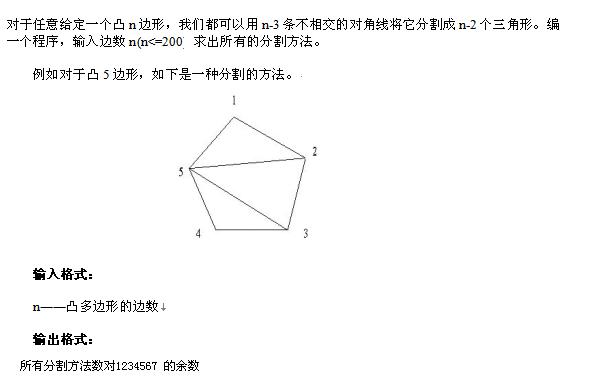
這道題拿道題沒有一點思路。我一直在想如何把問題變小，然而一無所獲（不是有漏項。就是有重復），最後不得不看了題解，發現這道dp題果然很詭異

設dp(i)表示i邊形的方案個數

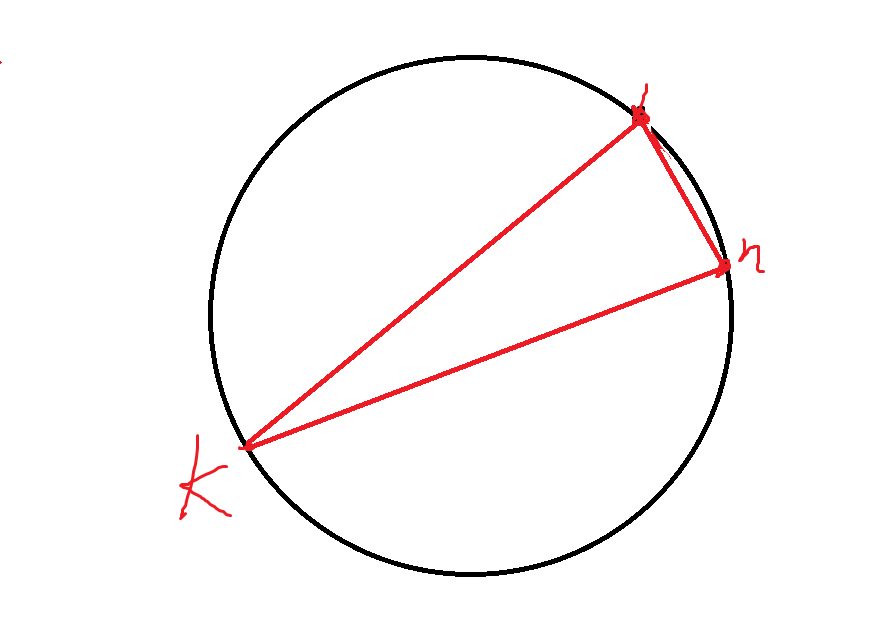
在一個i邊形中，任取兩個點，令一個點為1，一個點為i，那麽其他點為2——i-1

在點集{2--i-1}中任取一個點k

那麽連接k，1，n可以構成一個三角形

設上方區域為1區域三角形區域為2區域，下放區域為3區域

對於k說，設k左邊為r變形，k右邊為c變形

那麽對於k這個點的分割方案，就是

dp(r)*dp(c)
因為i邊形擁有點集{2--i-1}

那麽對於每一個點都有一種方案分割情況

所以狀態轉移方程就出來了dp(i)=∑dp(j)*dp(i-j+1)(1<=j<=i-1)(很神奇對不對)

後來才知道，這就是Catalan數，高興，終於推出來了

下面附上代碼

#include<cstdio>
#define N 200+10
long long f[N], n;
using namespace std;
long long dp(int i)
{
    if(i==2 or i==3 )return f[i]=1;
    if(f[i])return f[i];
    long long t=0;
    for(int j=2;j<=i-1;j++)
    {
////        printf("1\n");
        t=(t+dp(j)*dp(i-j+1
 
))%1234567;
    }
    return f[i]=t;
}
int main()
{
    scanf("%lld",&n);
    printf("%lld",dp(n));
    return 0;
}

Catalan數應用很多，作為一個oier，應該好好掌握

附上一個講解Catalan數的blog http://www.cnblogs.com/yaozhongxiao/archive/2009/11/10/1600516.html

詭異的dp（凸多邊形分割）：catalan數