軟件工程第一次作業——數獨的求解與生成
代碼的GitHub地址:https://github.com/Liu-SD/sudoku
| personal software process stages | 預估耗時 | 實際耗時 |
| 計劃 | ||
| 估計這個任務需要多少時間 | 10 min | 10 min |
| 開發 | ||
| 需求分析(包括學習新技術) | 180 min | 190 min |
| 生成設計文檔 | 0 min(沒做設計文檔) | 0 min |
| 設計復審(和同事審核設計文檔) | 0 min(沒有同事復審) | 0 min |
| 代碼規範(為目前的開發制定合適的規範) | 30 min | 60 min |
| 具體設計 | 180 min | 180 min |
| 具體編碼 | 240 min | 240 min |
| 代碼復審 | 60 min | 180 min |
| 測試(自我測試,修改代碼,提交修改) | 60 min | 50 min |
| 報告 | ||
| 測試報告 | 180 min | 180 min |
| 計算工作量 | 0 min(沒有做這項工作) | 0 min |
| 事後總結,並提出過程改進計劃 | 30 min | 30 min |
| 合計 | 1070 min | 1160 min |
解題思路描述
題目要求分為兩個部分,一個是解數獨,一個是自動生成數獨。並且生成數獨時對第一個數字做出了限制。所以可以認為自動生成數獨是只有一個數字限制時的解數獨。所以說這兩者大部分的實現算法是相同的。解數獨時是在找到第一個解的時候返回真,而生成數獨是在找到第N個解時返回真。
因此問題轉換為在R個限制條件(1<=R<=81)的情況下尋找到N(1<=N<=1000000)個解時返回真,否則返回假。解的輸出可以把輸出流作為參數傳入,找到一個答案時將答案輸出。這個問題是典型的回溯問題,在網上查資料了解到可以將問題轉化為精確覆蓋問題,使用DLX(dancing link)算法實現。DLX的重點在於十字鏈表的實現。
設計實現過程
實現算法的第一步需要使用十字鏈表表示稀疏矩陣。我把十字鏈表封裝為cross_link類,這個類,類中包括build方法,建立空的矩陣。build函數在構造函數中調用。稀疏矩陣建立以後,head指向矩陣頭,rows數組存放行的頭指針,cols數組存放列的頭指針。類中包括insert方法插入元素。delrow,delcol,recoverrow,recovercol四個方法刪除或恢復整行或整列。這四個方法將是算法實現的關鍵。在刪除行(列)時,修改每一行(列)中元素的鄰居節點到另一側,同時保留被刪除行(列)的鄰居指針,方便恢復。刪除和恢復需要以棧的方式操作。即後刪除的先恢復。
算法被封裝到dlx類中,dlx類調用並維護cross_link類的實例。類中的find_one和find_many實現解數獨和生成數獨兩個需求。find_one調用_find_one遞歸函數,find_many調用_find_many遞歸函數。
_find_one函數流程:
1. 如果head的右結點為空,即矩陣沒有列,則將result數組結果輸出,stack中的所有刪除操作使用recover做逆操作,即恢復為最初始的矩陣。返回真。
2. 否則,找到元素最少的列min_col_index,對於這一列的每一個元素i:
將元素i所在行壓如result棧中。
對於元素i所在行的每個元素j:
對於元素j所在列的每個元素p:
刪除p所在的行,壓如stack棧中。
刪除j所在的列,壓如stack棧中。
以stack和result棧的棧頂指針為參數遞歸調用自己,如果為真,返回真。
否則,把元素i從result棧彈出。
把這一次壓如stack棧中的元素彈出並且recover函數恢復刪除的行和列。
函數最後返回假。
_find_many函數和_find_one類似,在找到結果時將結果輸出到文件,計數器加一,在計數器等於目標數目之前都一直返回假。
十字鏈表的搭建容易出錯,而且增刪操作對於之後的算法十分重要,因此單元測試的重點放在了十字鏈表類的測試。設計單元測試時,先測試十字鏈表的插入操作,每插入一個元素,就計算元素個數並且斷言。之後測試鏈表的刪除行(列)以及之後行(列)的復原。
程序性能改進
我在程序性能改進方面沒有做很多的操作,僅僅將輸出到文件的部分從逐個數字寫入改為了一個數獨盤的一次性寫入。但這個改進大大提升了程序的性能。生成一百萬個數獨從之前的五分鐘變為當前的十四秒。
於是,進一步的,我修改了從文件讀入的方式,將之前的逐個數字讀入改為逐行讀入。
生成一百萬個數獨時,VS性能分析圖:
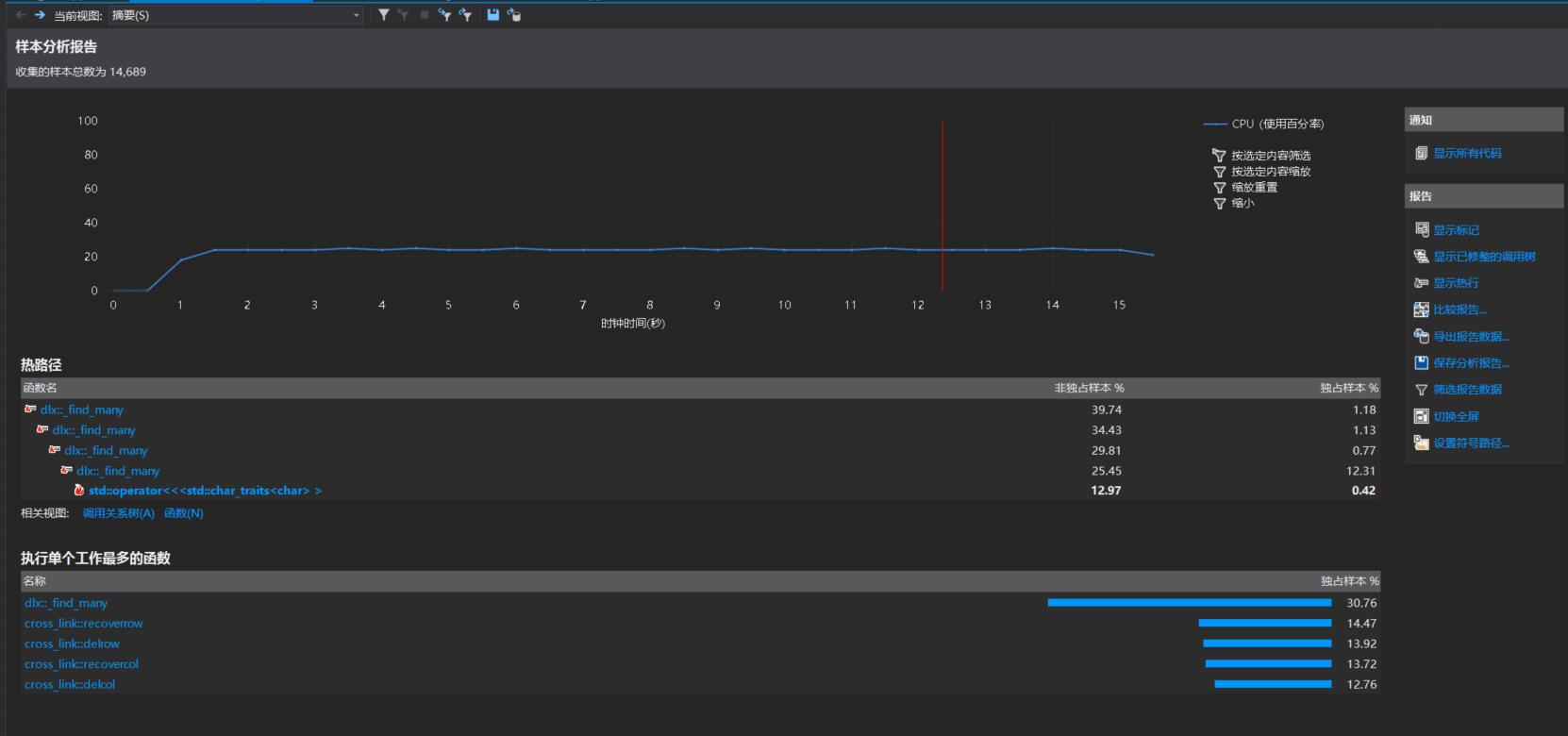
執行次數最多的函數為:
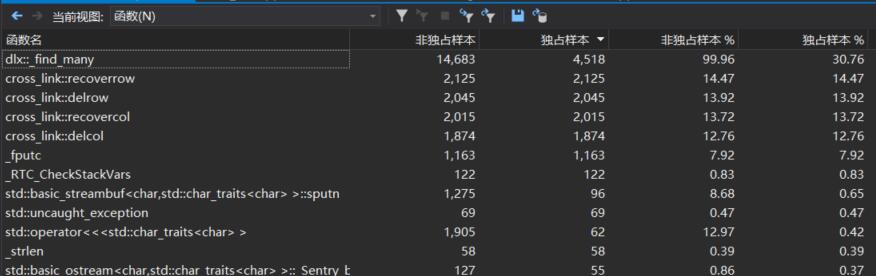
由此可見遞歸調用_find_many的執行次數最多,對鏈表的四個操作十分頻繁,對其進行優化十分重要。
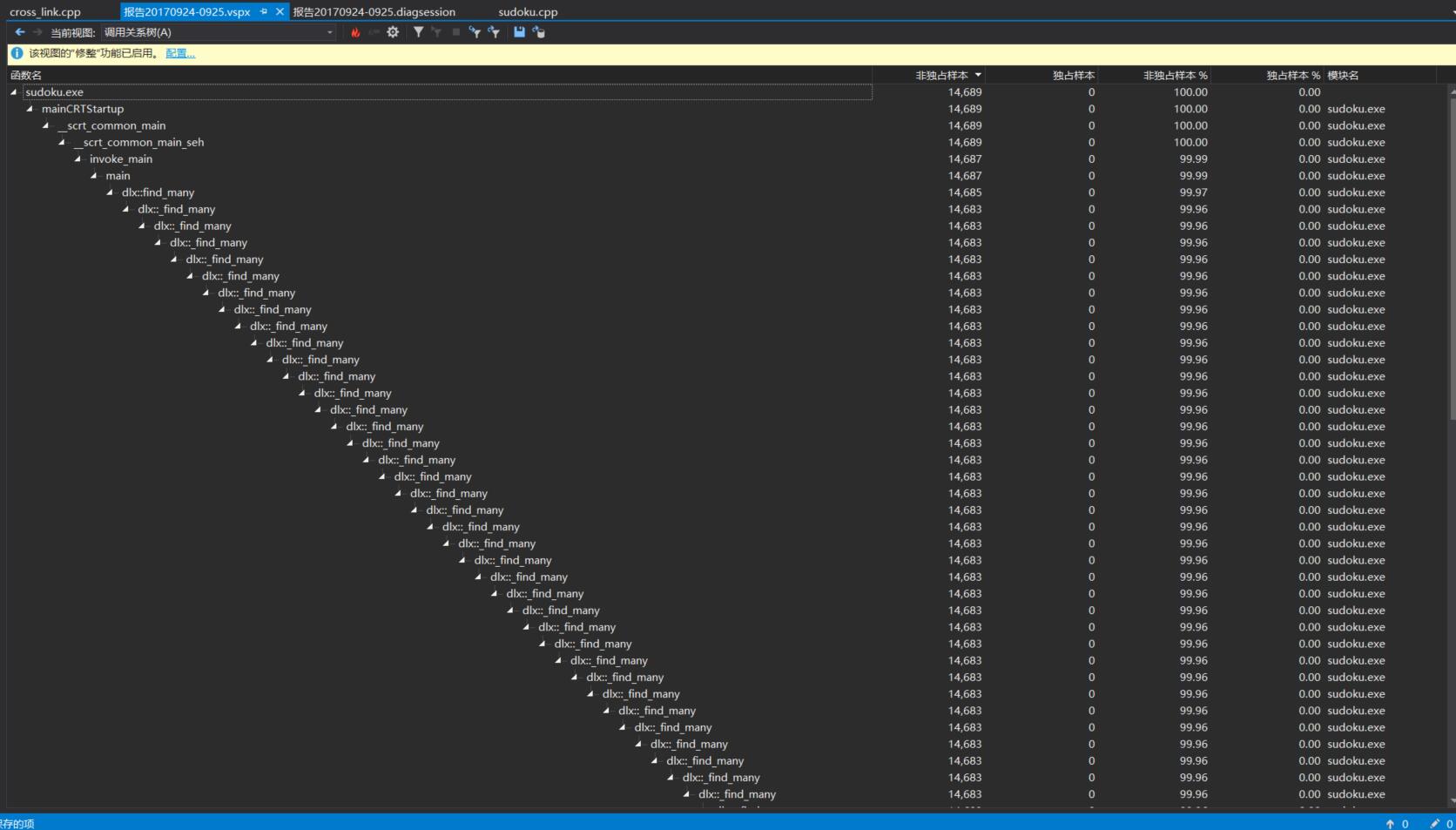
上圖是遞歸調用的函數關系圖。
代碼說明
十字鏈表類的關鍵代碼為刪除和恢復行或者列。
void cross_link::delrow(int r) { for (Cross i = rows[r]; i != NULL; i = i->right) { // 對於該行每一個元素 cols[i->col]->count--; // 刪除後該列的計數器減一 if (i->up) i->up->down = i->down; // 在它上方存在元素的情況下,上方元素改為指向該元素下方元素 if (i->down) i->down->up = i->up; // 下方元素同理 } } void cross_link::recoverrow(int r) { for (Cross i = rows[r]; i != NULL; i = i->right) { // 對於該行每一個元素 cols[i->col]->count++; // 恢復後該列的計數器加一 if (i->up) i->up->down = i; // 在上方元素不空的情況下,將原本指向自己下方的上方元素指回自己 if (i->down) i->down->up = i; // 下方元素同理 } }
以上是行的刪除和恢復一行元素的代碼,刪除恢復列的情形和一上代碼類似。
dlx類的關鍵代碼為函數的遞歸調用。以下是_find_many的代碼:
1 bool dlx::_find_many(int stack_top, int result_pos, int N, int & n, std::ofstream &fout) 2 { 3 if (!head->right) { // 在鏈表不存在列的情況下, 4 int matrix[9][9]; 5 for (int i = 0; i < 81; i++) { // 將result數組裏面的解翻譯為9*9的矩陣 6 int j = result[i] - 1; 7 int val = j % 9 + 1; 8 int pos = j / 9; 9 int row = pos / 9; 10 int col = pos % 9; 11 matrix[row][col] = val; 12 } 13 char str[19 * 9 + 2] = { 0 }; 14 for (int i = 0; i < 9; i++) { // 用字符串記錄矩陣並輸出到文件 15 for (int j = 0; j < 9; j++) { 16 str[i * 19 + 2 * j] = matrix[i][j] + ‘0‘; 17 str[i * 19 + 2 * j + 1] = ‘ ‘; 18 } 19 str[i * 19 + 18] = ‘\n‘; 20 } 21 str[19 * 9] = ‘\n‘; 22 str[19 * 9 + 1] = ‘\0‘; 23 fout << str; 24 if (++n >= N) // 計數器加一,如果大於要求的數量,返回真,否則返回假 25 return true; 26 else 27 return false; 28 } 29 int min_col_count = 100; 30 int min_col_index = -1; 31 for (Cross p = head->right; p != NULL; p = p->right) { // 找到元素最少的列 32 if (min_col_count > p->count) { 33 min_col_count = p->count; 34 min_col_index = p->col; 35 } 36 } 37 for (Cross a = cols[min_col_index]->down; a != NULL; a = a->down) { // 對於該列的所有元素 38 result[result_pos++] = a->row; // 將該元素的行號壓如result棧中 39 int new_stack_top = stack_top; 40 for (Cross b = rows[a->row]->right; b != NULL; b = b->right) { // 對於該元素所在行的所有元素 41 for (Cross c = cols[b->col]->down; c != NULL; c = c->down) { // 對於該元素所在列的所有元素 42 A->delrow(c->row); // 刪除該元素所在行 43 stack[new_stack_top++] = c->row; // 並記錄下刪除操作(刪除行時壓入正的行號,刪除列時壓入負的列號) 44 } 45 A->delcol(b->col); // 刪除該元素所在列 46 stack[new_stack_top++] = -b->col; // 記錄刪除操作 47 } 48 if (_find_many(new_stack_top, result_pos, N, n, fout)) // 調用下一級函數,如果找到的數獨數量達到了需求,則返回真 49 return true; 50 for (int i = new_stack_top - 1; i >= stack_top; i--) { // 否則將壓入stack棧中的刪除操作彈出,並且做其逆操作 51 if (stack[i] > 0) 52 A->recoverrow(stack[i]); 53 else 54 A->recovercol(-stack[i]); 55 } 56 result_pos--; // 最後將部分解從result數組中彈出,進入下一輪循環 57 } 58 return false;在循環完所有情況還沒有達到數量需求的情況下,返回假 59 }
以下是_find_one的代碼:
1 bool dlx::_find_one(int stack_top, int result_pos) 2 { 3 if (!head->right) { // 找到一個解時記錄答案並且直接返回真 4 for (int i = stack_top - 1; i >= 0; i--) { 5 if (stack[i] > 0) 6 A->recoverrow(stack[i]); 7 else 8 A->recovercol(-stack[i]); 9 } 10 return true; 11 } 12 int min_col_count = 100; 13 int min_col_index = -1; 14 for (Cross p = head->right; p != NULL; p = p->right) { 15 if (min_col_count > p->count) { 16 min_col_count = p->count; 17 min_col_index = p->col; 18 } 19 } 26 for (Cross a = cols[min_col_index]->down; a != NULL; a = a->down) { 27 result[result_pos++] = a->row; 28 int new_stack_top = stack_top; 29 for (Cross b = rows[a->row]->right; b != NULL; b = b->right) { 30 for (Cross c = cols[b->col]->down; c != NULL; c = c->down) { 31 A->delrow(c->row); 32 stack[new_stack_top++] = c->row; 33 } 34 A->delcol(b->col); 35 stack[new_stack_top++] = -b->col; 36 } 37 if (_find_one(new_stack_top, result_pos)) 38 return true; 39 for (int i = new_stack_top - 1; i >= stack_top; i--) { 40 if (stack[i] > 0) 41 A->recoverrow(stack[i]); 42 else 43 A->recovercol(-stack[i]); 44 } 45 result_pos--; 46 } 47 return false; 48 }
程序實現完成。_find_one和_find_many存在代碼冗余的現象,下一步修改目標是將冗余部分抽取出來或是將兩個函數合並為一個。
軟件工程第一次作業——數獨的求解與生成
